微专题 利用轴对称求最值问题- 2024年中考数学复习课件(共61张PPT)
文档属性
| 名称 | 微专题 利用轴对称求最值问题- 2024年中考数学复习课件(共61张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 16:38:51 | ||
图片预览










文档简介
(共61张PPT)
微专题 利用轴对称求最值问题
模型一 “一线两点”型(一动点 两定点)
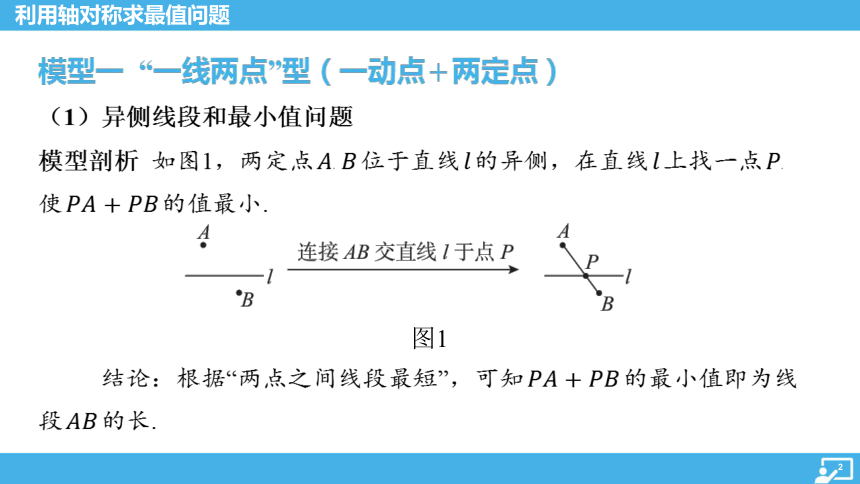
(1)异侧线段和最小值问题
模型剖析 如图1,两定点 , 位于直线 的异侧,在直线 上找一点 ,
使 的值最小.
图1
结论:根据“两点之间线段最短”,可知 的最小值即为线
段 的长.
模型应用
图2
1.(2020·贺州)如图2,四边形 是菱形,对角
线 , 相交于点 , , ,点
是 上一动点,点 是 的中点,则 的最
小值为_____.
图2
提示:连接 交 于点 ,则线段 的长即为
的最小值.由四边形 是菱形,得
, , ,
.在 中,
【答案】
,所以 .所以 是等边三角形.又
因为 是 的中点,所以 .故 , 是等边三角形 的两
条高线.所以 .
(2)同侧线段和最小值问题
模型剖析 如图3,两定点 , 位于直线 的同侧,在直线 上找一点 ,
使得 的值最小.
图3
解题思想:将两定点同侧问题,利用轴对称的性质转化为异侧问题,
即可利用(1)中模型解决.
结论:根据“两点之间线段最短”,可知 的最小值即为图中
线段 的长.
模型应用
图4
2.(2022·广安)如图4,菱形 的边长为2,点
是对角线 上的一个动点,点 , 分别为边 ,
的中点,则 的最小值是( ).
A.2 B. C.1.5 D.
图63
提示:如图63,取 的中点 ,
连接 , 四边形 是菱形, , , , , 四边形 是平行四边形. 四边形 是菱形,
【答案】A
, , 点 , 关于直线 对称.
, 的最小值为2.
图5
3.(2023·枣庄 节选)如图5,抛物线
经过 , 两点,并交 轴于另一点 ,点
是抛物线的顶点,直线 与 轴交于点 .
(1)求该抛物线的函数解析式.
解: 抛物线 经过 , 两点,
解得
该抛物线的函数解析式为 .
(2)若点 是 轴上一动点,分别连接 , ,求 的最小值.
图5
解 , 顶点 .
设直线 的函数解析式为 ,则
解得
直线 的函数解析式为 .
当 时, , .
,即 的长为 的最小值.
, 的最小值为 .
图64
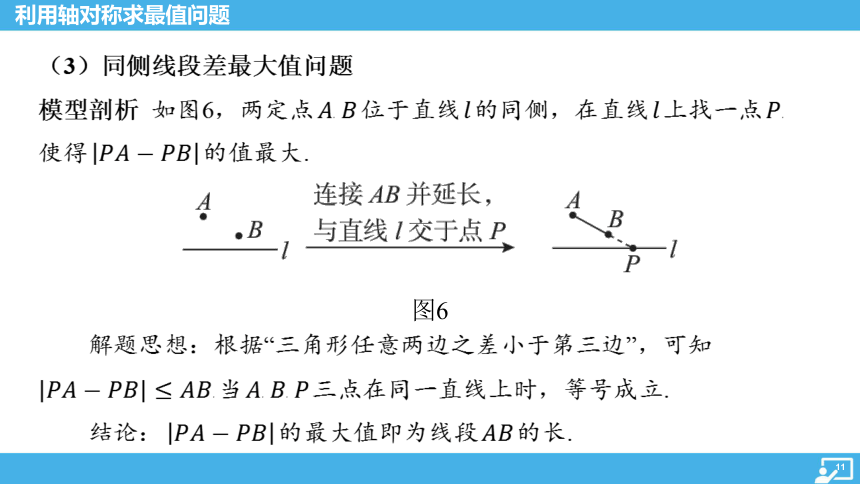
(3)同侧线段差最大值问题
模型剖析 如图6,两定点 , 位于直线 的同侧,在直线 上找一点 ,
使得 的值最大.
图6
解题思想:根据“三角形任意两边之差小于第三边”,可知
,当 , , 三点在同一直线上时,等号成立.
结论: 的最大值即为线段 的长.
模型应用
图7
4.如图7,在正方形 中, ,点 是对角线
上靠近点 的三等分点, 是 边上的一点,且
为 边上的一点,则 的最大值是
_____.
图65
小锦囊 当 , , 三点在同一直线上时, 的长即为 的最大值.
提示:如图65,延长 交 于点 ,此时 的值
最大,最大值为 的长. 点 是对角线 上靠近点 的
三等分点, .易证 ,所以
.又 , .过点 作 于点 ,则 , , .在 中, .由 ,得 ,所以 .
【答案】
(4)异侧线段差最大值问题
模型剖析 如图8,两定点 , 位于直线 的异侧,在直线 上找一点 ,
使得 的值最大.
图8
解题思想:将两定点异侧问题,利用轴对称的性质转化为同侧问题,
即可利用(3)中模型解决.
结论: 的最大值即为图中线段 的长.
模型应用
图9
5.如图9,在正方形 中, , 与 交于
点 , 是 的中点,点 在 边上,且 ,
为对角线 上一个动点,则 的最大值是___.
图66
小锦囊 作点 关于 的对称点 ,则 的长即为 的最大值.
提示:如图66,作点 关于 的对称点 ,
连接 ,并延长交 于点 ,连接 .由轴对称性质
知, ,此时 ,取得
最大值.因为四边形 是边长为8的正方形,所以点 在
上, .由 为 的中点,得
.因为 是 的中点,所以 ,则
, .因为 ,
所以 ,则 .所以 .又 ,所以 是等腰直角三角形,则 .所以 的最大值为2.
【答案】2
模型二 “一点两线”型(两动点 一定点)
图10
(1)周长最小型
模型剖析 如图10,点 是 内部一定点,在 上找一点 ,在
上找一点 ,使得 的周长最小.
解题思想:要使 的周长最小,即 的值最小,
只要利用轴对称的性质,将三条线段转化到同一直线上,根据“两点之
间线段最短”即可求解.
结论: 周长的最小值即为图中线段 的长.
图10
模型应用
图11
6.如图11,在 中, ,
,点 为 上一定点,点 , 分
别为边 , 上的动点.当 的周长最小
时, 的度数为____ .
图67
提示:如图67,作点 关于 的对称点 ,
点 关于 的对称点 ,连接 ,交 于点 ,
交 于点 ,此时 的周长最小.由轴对称的
性质,可知 , ,
, . .
. . 由轴对称的
【答案】90
性质,可知 , , ,
.
.
图12
7.(2022·遂宁 节选)如图12,在平面直角坐标系中,抛
物线 与 轴交于 , 两点,与 轴交于
点 ,其中点 的坐标为 ,点 的坐标为
为 的边 上的一动点, 为 边上的
一动点,点 的坐标为 .求 周长的最小值.
小锦囊 作点 关于直线 的对称点 ,点 关于直线 的
对称点 ,连接 ,由对称性可知,当点 , , , 共线时,
的周长最小,最小值为 的长.
图68
解: 抛物线 经过点 ,
,
抛物线的函数解析式为 .
如图68,作点 关于直线 的对称点 ,点 关于直线 的对称点 ,连接 , , , .
由对称性可知, , , 的周长, 当点 , , , 在同一直线上时, 的周长最小,最小值为 的长.
令 ,则 ,解得 或
是等腰直角三角形, .
垂直平分 , , .
是等腰直角三角形.
又 , ,
点 , 关于 轴对称,
.
的周长的最小值为 .
图68
图13
(2)两条线段之和最小型
模型剖析 如图13,点 是 内
部的一定点,在 上找一点 ,
在 上找一点 ,使得
的值最小.
解题思想:要使 的值最小,只要利用轴对称的性质,将
, 转化到同一直线上,根据“垂线段最短”即可求解.
结论: 的最小值即为图中 的长.
模型应用
图14
8.如图14,在菱形 中, , ,
点 是 边的中点, , 分别是 , 上的动点,
连接 , ,则 的最小值是( ).
A.6 B. C. D.4.5
图69
小锦囊 作点 关于 的对称点 ,过点 作 于点 ,交 于点 ,此时 的长即为 的最小值.
提示:如图69,作点 关于 的对称点 ,过点
作 于点 ,交 于点 ,此时 取
得最小值,且 四边形 是菱形,
点 在 上. , , .
由 ,得 ,解得
. 的最小值是 .
【答案】C
模型三 “两点两线”型(两动点 两定点)
图15
模型剖析 如图15,点 , 是
内部的两个定点,在 ,
上分别取点 , ,使得四边
形 的周长最小.
解题思想:考虑到 是定线段,因此只要考虑 的
最小值即可.类似地,利用轴对称的性质,将这3条线段转化到同一直线
上,根据“两点之间线段最短”即可求解.
结论:边形 周长的最小值即为图中 的值.
模型应用
图16
9.如图16,已知正方形 的边长为3,点 在 边上且
,点 , 分别是边 , 上的动点(均不与顶
点重合),则四边形 的周长的最小值是__________.
图70
小锦囊 作点 关于 的对称点 ,点 关于 的对称点 ,则 即为四边形 的周长的最小值.
, , , ,所以四边形
的周长 .在 中, ,所以四边形 的周长的最小值是 .
【答案】
微专题练习(十三)
利用轴对称求最值问题
模型一 “一线两点”型(一动点 两定点)
图1
1.如图1,等边三角形 的边长为4, 是 边上的高,
点 是 边的中点,点 是 上的动点,则线段
的最小值为( ).
A.2 B. C. D.4
图109
提示:由等边三角形“三线合一”的性质知,点 关于
的对称点是 .如图109,连接 ,交 于点 ,连接
,此时 的值最小,且
.因为点 是 边的中点,所
以 .所以 .所以
的最小值为 .
【答案】B
图2
2.(2022·赤峰)如图2,四边形 为菱形,
点 , , , 均在坐标轴上, ,
点 的坐标为 , 是 的中点, 是
上的一个动点,则 的最小值是( ).
A.3 B.5 C. D.
图110
提示:由菱形的对称性得,点 关于 轴的对称
点是 的中点 ,连接 交 于点 ,如图
110,此时 ,取得最小
值. 四边形 是菱形, ,
, , ,
【答案】A
, . 是等边三角形. ,即
的最小值是3.
图3
3.(2021·永州)如图3, , 两点的坐标分别
为 , .在 轴上找一点 ,使线段
的值最小,则点 的坐标是______.
图111
提示:如图111,连接 交 轴于点 .根据两点
之间线段最短,可知点 即为所求.设直线 的
函数解析式为 ,把 ,
代入,得 解得
.当 时, .
图4
4.如图4,在矩形 中, , ,连接
, 是 的中点, 是 上一点,且
, 是 上一动点,则 的最大值
为_ ___.
图112
提示:在矩形 中, , ,
.如图112,连接 并延长交 于点 ,此时 的值最大,最大值为 的长.
, .又 , , ,
. 过点 作 于点 ,则四边形 是矩形. ,
. ,即
的最大值为 .
【答案】
图5
5.如图5,在菱形 中, , , 与 交于点 ,点 在 上且 ,点 在 上且 , 为对角线 上一点,则 的最大值为___.
图113
提示:如图113,作点 关于直线 的对称点 ,连
接 , .由轴对称的性质,可得 ,
.当 , , 三点在同一直线上时, ,取得最大值.在菱形 中, , ,
, , .又 ,
, , ,
.又 , 是等边三角形.
,即 的最大值是2.
【答案】2
图6
6.如图6,在边长为4的正方形 中, 是 边上的
一点,且 ,点 为对角线 上的动点,则
的周长的最小值为___.
图114
提示:如图114,过点 作 于点 ,延长 交
于点 ,连接 交 于点 ,连接 四边形
为正方形, .
. ,即点 与点
关于 对称. 当点 与点 重合时,
【答案】6
的周长取得最小值,最小值为 的长. 正方形 的
边长为4, , , ,
.
图7
7.(2022·贺州)如图7,在矩形 中, ,
, , 分别是 , 的中点, 的平分线
交 于点 ,点 是线段 上的一个动点,则 的
周长的最小值为_________.
图115
提示:如图115,在 上截取 ,使得 ,连接
,过点 作 于点 四边形 是矩
形, .又 , 四边形
是矩形. ,
, ,
,
. 平分 , , 点 , 关于 对称. .
, 的周长的最小值为
.
【答案】
图115
图8
8.(2022·常德 节选)如图8,已知抛物线经过点 ,
,且它的对称轴为直线 ,点 的坐标为
, 是抛物线上的动点,当 的值最大时,点
的坐标为________, 的最大值是_____.
小锦囊 当 , , 三点在同一直线上,且不重合时, 的长即为 的最大值.
图116
提示: 抛物线过点 ,且它的对称轴为直线
, 抛物线与 轴的另一个交点的坐标为 .设抛
物线的函数解析式为 ,把 代入,得
.解得 .设直线
的函数解析式为 ,把 , 代入,
得 解得 直线 的函数解析式
为 .当 的值最大时,点 , , 在同一直线上,如图116.联立方程,得 解得 或 .此时 .
【答案】 ;
图116
图9
9.(2023·宁夏 节选)如图9,抛物线
与 轴交于 , 两点,
与 轴交于点 .已知点 的坐标是 ,抛物线
的对称轴是直线 .
(1)直接写出点 的坐标.
解:点 的坐标是 .
(2)在对称轴上找一点 ,使 的值最小.求点 的坐标和
的最小值.
图9
图117
解:如图117,连接 ,线段 与直线
的交点就是所求作的点 .
把 , 代入抛物线函数解析式 ,得
解得
抛物线的函数解析式为 .
令 ,得
.
设直线 的函数解析式为 ,把 , 代入,
得
解得
直线 的函数解析式为 .
当 时,
, .
图117
点 , 关于直线 对称,
.
的最小值为 .
图117
模型二 “一点两线”型(两动点 一定点)
图10
10.如图10,在五边形 中, 为钝
角 , ,在 , 上分别找一点 ,
,当 的周长最小时, 的度数为( ).
A. B. C. D.
图118
提示:如图118,作点 关于 的对称点 ,
作点 关于 的对称点 .连接 ,分别
交线段 和线段 于点 , ,连接 ,
,则 , ,此时
的周长取最小值. ,
, ,
,
,
.
,
.
【答案】C
图118
图11
11.(2021·绥化)如图11,已知在
中, , , ,点
为边 上的动点,点 为边 上的动点,则
的最小值是( ).
A. B. C. D.
图119
提示: , ,
.
如图119,作点 关于 的对称点 ,延长 ,
交于点 , ,
当
【答案】B
, , 三点在同一直线上且与 垂直时, 取得最小
值.作 于点 ,则 长即为 的最小值.在
中, .
图12
12.(2022·娄底)如图12,菱形 的边长为2,
, , 分别是 , 上的动点,
则 的最小值为____.
图120
提示:如图120,连接 ,作 于点 , 四边形 是菱形, , .又 ,
当 , , 三点在同一直线上,且与 垂直时,
【答案】
取得最小值,最小值为 的长. , ,
. 的最小值为 .
模型三 “两点两线”型(两动点 两定点)
图13
13.(2021·聊城)如图13,在平面直角坐标系中,矩形
的顶点 在坐标原点,顶点 , 分别在 轴、 轴
上, , 两点的坐标分别为 , ,线段 在
边 上移动,保持 .当四边形 的周长最小时,
点 的坐标是________.
图121
提示:如图121,在 上截取 ,作点 关于 轴的
对称点 ,连接 交 于点 ,则 .又因
为 ,所以四边形 是平行四边形,则
.因为点 与点 关于 轴对称,所以 ,
且点 的坐标为 .因为四边形 的周长
, 和
的长是定值,所以当 有最小值时,四边形
的周长有最小值.所以当 , , 三点在同一直线上时, 有
最小值.因为点 的坐标为 ,所以点 的坐标为 .设直线
的函数解析式为 ,则 解得 所以直线 的函数解析式为 .当 时, ,所以 .
【答案】
图121
微专题 利用轴对称求最值问题
模型一 “一线两点”型(一动点 两定点)
(1)异侧线段和最小值问题
模型剖析 如图1,两定点 , 位于直线 的异侧,在直线 上找一点 ,
使 的值最小.
图1
结论:根据“两点之间线段最短”,可知 的最小值即为线
段 的长.
模型应用
图2
1.(2020·贺州)如图2,四边形 是菱形,对角
线 , 相交于点 , , ,点
是 上一动点,点 是 的中点,则 的最
小值为_____.
图2
提示:连接 交 于点 ,则线段 的长即为
的最小值.由四边形 是菱形,得
, , ,
.在 中,
【答案】
,所以 .所以 是等边三角形.又
因为 是 的中点,所以 .故 , 是等边三角形 的两
条高线.所以 .
(2)同侧线段和最小值问题
模型剖析 如图3,两定点 , 位于直线 的同侧,在直线 上找一点 ,
使得 的值最小.
图3
解题思想:将两定点同侧问题,利用轴对称的性质转化为异侧问题,
即可利用(1)中模型解决.
结论:根据“两点之间线段最短”,可知 的最小值即为图中
线段 的长.
模型应用
图4
2.(2022·广安)如图4,菱形 的边长为2,点
是对角线 上的一个动点,点 , 分别为边 ,
的中点,则 的最小值是( ).
A.2 B. C.1.5 D.
图63
提示:如图63,取 的中点 ,
连接 , 四边形 是菱形, , , , , 四边形 是平行四边形. 四边形 是菱形,
【答案】A
, , 点 , 关于直线 对称.
, 的最小值为2.
图5
3.(2023·枣庄 节选)如图5,抛物线
经过 , 两点,并交 轴于另一点 ,点
是抛物线的顶点,直线 与 轴交于点 .
(1)求该抛物线的函数解析式.
解: 抛物线 经过 , 两点,
解得
该抛物线的函数解析式为 .
(2)若点 是 轴上一动点,分别连接 , ,求 的最小值.
图5
解 , 顶点 .
设直线 的函数解析式为 ,则
解得
直线 的函数解析式为 .
当 时, , .
,即 的长为 的最小值.
, 的最小值为 .
图64
(3)同侧线段差最大值问题
模型剖析 如图6,两定点 , 位于直线 的同侧,在直线 上找一点 ,
使得 的值最大.
图6
解题思想:根据“三角形任意两边之差小于第三边”,可知
,当 , , 三点在同一直线上时,等号成立.
结论: 的最大值即为线段 的长.
模型应用
图7
4.如图7,在正方形 中, ,点 是对角线
上靠近点 的三等分点, 是 边上的一点,且
为 边上的一点,则 的最大值是
_____.
图65
小锦囊 当 , , 三点在同一直线上时, 的长即为 的最大值.
提示:如图65,延长 交 于点 ,此时 的值
最大,最大值为 的长. 点 是对角线 上靠近点 的
三等分点, .易证 ,所以
.又 , .过点 作 于点 ,则 , , .在 中, .由 ,得 ,所以 .
【答案】
(4)异侧线段差最大值问题
模型剖析 如图8,两定点 , 位于直线 的异侧,在直线 上找一点 ,
使得 的值最大.
图8
解题思想:将两定点异侧问题,利用轴对称的性质转化为同侧问题,
即可利用(3)中模型解决.
结论: 的最大值即为图中线段 的长.
模型应用
图9
5.如图9,在正方形 中, , 与 交于
点 , 是 的中点,点 在 边上,且 ,
为对角线 上一个动点,则 的最大值是___.
图66
小锦囊 作点 关于 的对称点 ,则 的长即为 的最大值.
提示:如图66,作点 关于 的对称点 ,
连接 ,并延长交 于点 ,连接 .由轴对称性质
知, ,此时 ,取得
最大值.因为四边形 是边长为8的正方形,所以点 在
上, .由 为 的中点,得
.因为 是 的中点,所以 ,则
, .因为 ,
所以 ,则 .所以 .又 ,所以 是等腰直角三角形,则 .所以 的最大值为2.
【答案】2
模型二 “一点两线”型(两动点 一定点)
图10
(1)周长最小型
模型剖析 如图10,点 是 内部一定点,在 上找一点 ,在
上找一点 ,使得 的周长最小.
解题思想:要使 的周长最小,即 的值最小,
只要利用轴对称的性质,将三条线段转化到同一直线上,根据“两点之
间线段最短”即可求解.
结论: 周长的最小值即为图中线段 的长.
图10
模型应用
图11
6.如图11,在 中, ,
,点 为 上一定点,点 , 分
别为边 , 上的动点.当 的周长最小
时, 的度数为____ .
图67
提示:如图67,作点 关于 的对称点 ,
点 关于 的对称点 ,连接 ,交 于点 ,
交 于点 ,此时 的周长最小.由轴对称的
性质,可知 , ,
, . .
. . 由轴对称的
【答案】90
性质,可知 , , ,
.
.
图12
7.(2022·遂宁 节选)如图12,在平面直角坐标系中,抛
物线 与 轴交于 , 两点,与 轴交于
点 ,其中点 的坐标为 ,点 的坐标为
为 的边 上的一动点, 为 边上的
一动点,点 的坐标为 .求 周长的最小值.
小锦囊 作点 关于直线 的对称点 ,点 关于直线 的
对称点 ,连接 ,由对称性可知,当点 , , , 共线时,
的周长最小,最小值为 的长.
图68
解: 抛物线 经过点 ,
,
抛物线的函数解析式为 .
如图68,作点 关于直线 的对称点 ,点 关于直线 的对称点 ,连接 , , , .
由对称性可知, , , 的周长, 当点 , , , 在同一直线上时, 的周长最小,最小值为 的长.
令 ,则 ,解得 或
是等腰直角三角形, .
垂直平分 , , .
是等腰直角三角形.
又 , ,
点 , 关于 轴对称,
.
的周长的最小值为 .
图68
图13
(2)两条线段之和最小型
模型剖析 如图13,点 是 内
部的一定点,在 上找一点 ,
在 上找一点 ,使得
的值最小.
解题思想:要使 的值最小,只要利用轴对称的性质,将
, 转化到同一直线上,根据“垂线段最短”即可求解.
结论: 的最小值即为图中 的长.
模型应用
图14
8.如图14,在菱形 中, , ,
点 是 边的中点, , 分别是 , 上的动点,
连接 , ,则 的最小值是( ).
A.6 B. C. D.4.5
图69
小锦囊 作点 关于 的对称点 ,过点 作 于点 ,交 于点 ,此时 的长即为 的最小值.
提示:如图69,作点 关于 的对称点 ,过点
作 于点 ,交 于点 ,此时 取
得最小值,且 四边形 是菱形,
点 在 上. , , .
由 ,得 ,解得
. 的最小值是 .
【答案】C
模型三 “两点两线”型(两动点 两定点)
图15
模型剖析 如图15,点 , 是
内部的两个定点,在 ,
上分别取点 , ,使得四边
形 的周长最小.
解题思想:考虑到 是定线段,因此只要考虑 的
最小值即可.类似地,利用轴对称的性质,将这3条线段转化到同一直线
上,根据“两点之间线段最短”即可求解.
结论:边形 周长的最小值即为图中 的值.
模型应用
图16
9.如图16,已知正方形 的边长为3,点 在 边上且
,点 , 分别是边 , 上的动点(均不与顶
点重合),则四边形 的周长的最小值是__________.
图70
小锦囊 作点 关于 的对称点 ,点 关于 的对称点 ,则 即为四边形 的周长的最小值.
, , , ,所以四边形
的周长 .在 中, ,所以四边形 的周长的最小值是 .
【答案】
微专题练习(十三)
利用轴对称求最值问题
模型一 “一线两点”型(一动点 两定点)
图1
1.如图1,等边三角形 的边长为4, 是 边上的高,
点 是 边的中点,点 是 上的动点,则线段
的最小值为( ).
A.2 B. C. D.4
图109
提示:由等边三角形“三线合一”的性质知,点 关于
的对称点是 .如图109,连接 ,交 于点 ,连接
,此时 的值最小,且
.因为点 是 边的中点,所
以 .所以 .所以
的最小值为 .
【答案】B
图2
2.(2022·赤峰)如图2,四边形 为菱形,
点 , , , 均在坐标轴上, ,
点 的坐标为 , 是 的中点, 是
上的一个动点,则 的最小值是( ).
A.3 B.5 C. D.
图110
提示:由菱形的对称性得,点 关于 轴的对称
点是 的中点 ,连接 交 于点 ,如图
110,此时 ,取得最小
值. 四边形 是菱形, ,
, , ,
【答案】A
, . 是等边三角形. ,即
的最小值是3.
图3
3.(2021·永州)如图3, , 两点的坐标分别
为 , .在 轴上找一点 ,使线段
的值最小,则点 的坐标是______.
图111
提示:如图111,连接 交 轴于点 .根据两点
之间线段最短,可知点 即为所求.设直线 的
函数解析式为 ,把 ,
代入,得 解得
.当 时, .
图4
4.如图4,在矩形 中, , ,连接
, 是 的中点, 是 上一点,且
, 是 上一动点,则 的最大值
为_ ___.
图112
提示:在矩形 中, , ,
.如图112,连接 并延长交 于点 ,此时 的值最大,最大值为 的长.
, .又 , , ,
. 过点 作 于点 ,则四边形 是矩形. ,
. ,即
的最大值为 .
【答案】
图5
5.如图5,在菱形 中, , , 与 交于点 ,点 在 上且 ,点 在 上且 , 为对角线 上一点,则 的最大值为___.
图113
提示:如图113,作点 关于直线 的对称点 ,连
接 , .由轴对称的性质,可得 ,
.当 , , 三点在同一直线上时, ,取得最大值.在菱形 中, , ,
, , .又 ,
, , ,
.又 , 是等边三角形.
,即 的最大值是2.
【答案】2
图6
6.如图6,在边长为4的正方形 中, 是 边上的
一点,且 ,点 为对角线 上的动点,则
的周长的最小值为___.
图114
提示:如图114,过点 作 于点 ,延长 交
于点 ,连接 交 于点 ,连接 四边形
为正方形, .
. ,即点 与点
关于 对称. 当点 与点 重合时,
【答案】6
的周长取得最小值,最小值为 的长. 正方形 的
边长为4, , , ,
.
图7
7.(2022·贺州)如图7,在矩形 中, ,
, , 分别是 , 的中点, 的平分线
交 于点 ,点 是线段 上的一个动点,则 的
周长的最小值为_________.
图115
提示:如图115,在 上截取 ,使得 ,连接
,过点 作 于点 四边形 是矩
形, .又 , 四边形
是矩形. ,
, ,
,
. 平分 , , 点 , 关于 对称. .
, 的周长的最小值为
.
【答案】
图115
图8
8.(2022·常德 节选)如图8,已知抛物线经过点 ,
,且它的对称轴为直线 ,点 的坐标为
, 是抛物线上的动点,当 的值最大时,点
的坐标为________, 的最大值是_____.
小锦囊 当 , , 三点在同一直线上,且不重合时, 的长即为 的最大值.
图116
提示: 抛物线过点 ,且它的对称轴为直线
, 抛物线与 轴的另一个交点的坐标为 .设抛
物线的函数解析式为 ,把 代入,得
.解得 .设直线
的函数解析式为 ,把 , 代入,
得 解得 直线 的函数解析式
为 .当 的值最大时,点 , , 在同一直线上,如图116.联立方程,得 解得 或 .此时 .
【答案】 ;
图116
图9
9.(2023·宁夏 节选)如图9,抛物线
与 轴交于 , 两点,
与 轴交于点 .已知点 的坐标是 ,抛物线
的对称轴是直线 .
(1)直接写出点 的坐标.
解:点 的坐标是 .
(2)在对称轴上找一点 ,使 的值最小.求点 的坐标和
的最小值.
图9
图117
解:如图117,连接 ,线段 与直线
的交点就是所求作的点 .
把 , 代入抛物线函数解析式 ,得
解得
抛物线的函数解析式为 .
令 ,得
.
设直线 的函数解析式为 ,把 , 代入,
得
解得
直线 的函数解析式为 .
当 时,
, .
图117
点 , 关于直线 对称,
.
的最小值为 .
图117
模型二 “一点两线”型(两动点 一定点)
图10
10.如图10,在五边形 中, 为钝
角 , ,在 , 上分别找一点 ,
,当 的周长最小时, 的度数为( ).
A. B. C. D.
图118
提示:如图118,作点 关于 的对称点 ,
作点 关于 的对称点 .连接 ,分别
交线段 和线段 于点 , ,连接 ,
,则 , ,此时
的周长取最小值. ,
, ,
,
,
.
,
.
【答案】C
图118
图11
11.(2021·绥化)如图11,已知在
中, , , ,点
为边 上的动点,点 为边 上的动点,则
的最小值是( ).
A. B. C. D.
图119
提示: , ,
.
如图119,作点 关于 的对称点 ,延长 ,
交于点 , ,
当
【答案】B
, , 三点在同一直线上且与 垂直时, 取得最小
值.作 于点 ,则 长即为 的最小值.在
中, .
图12
12.(2022·娄底)如图12,菱形 的边长为2,
, , 分别是 , 上的动点,
则 的最小值为____.
图120
提示:如图120,连接 ,作 于点 , 四边形 是菱形, , .又 ,
当 , , 三点在同一直线上,且与 垂直时,
【答案】
取得最小值,最小值为 的长. , ,
. 的最小值为 .
模型三 “两点两线”型(两动点 两定点)
图13
13.(2021·聊城)如图13,在平面直角坐标系中,矩形
的顶点 在坐标原点,顶点 , 分别在 轴、 轴
上, , 两点的坐标分别为 , ,线段 在
边 上移动,保持 .当四边形 的周长最小时,
点 的坐标是________.
图121
提示:如图121,在 上截取 ,作点 关于 轴的
对称点 ,连接 交 于点 ,则 .又因
为 ,所以四边形 是平行四边形,则
.因为点 与点 关于 轴对称,所以 ,
且点 的坐标为 .因为四边形 的周长
, 和
的长是定值,所以当 有最小值时,四边形
的周长有最小值.所以当 , , 三点在同一直线上时, 有
最小值.因为点 的坐标为 ,所以点 的坐标为 .设直线
的函数解析式为 ,则 解得 所以直线 的函数解析式为 .当 时, ,所以 .
【答案】
图121
同课章节目录
