微专题 全等三角形的六种基本模型-2024年中考数学复习课件(共40张PPT)
文档属性
| 名称 | 微专题 全等三角形的六种基本模型-2024年中考数学复习课件(共40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 17:30:40 | ||
图片预览





文档简介
(共40张PPT)
微专题 全等三角形的六种基本模型
模型一 平移型
模型剖析
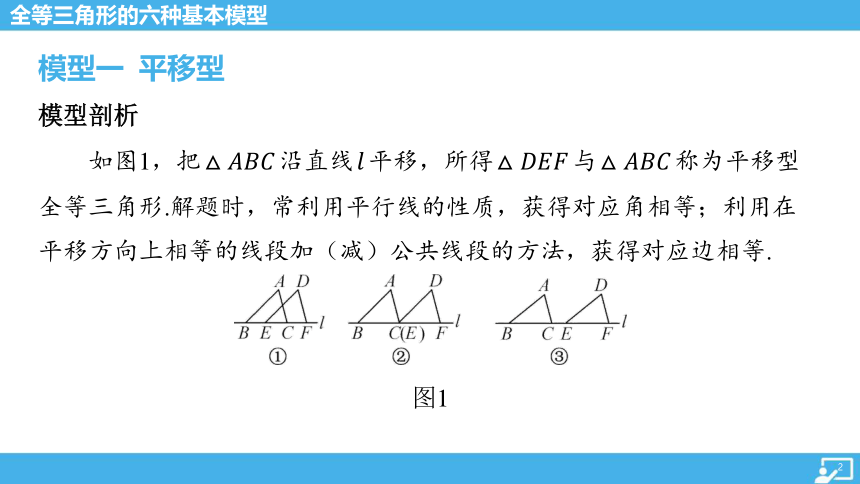
如图1,把 沿直线 平移,所得 与 称为平移型
全等三角形.解题时,常利用平行线的性质,获得对应角相等;利用在
平移方向上相等的线段加(减)公共线段的方法,获得对应边相等.
图1
模型应用
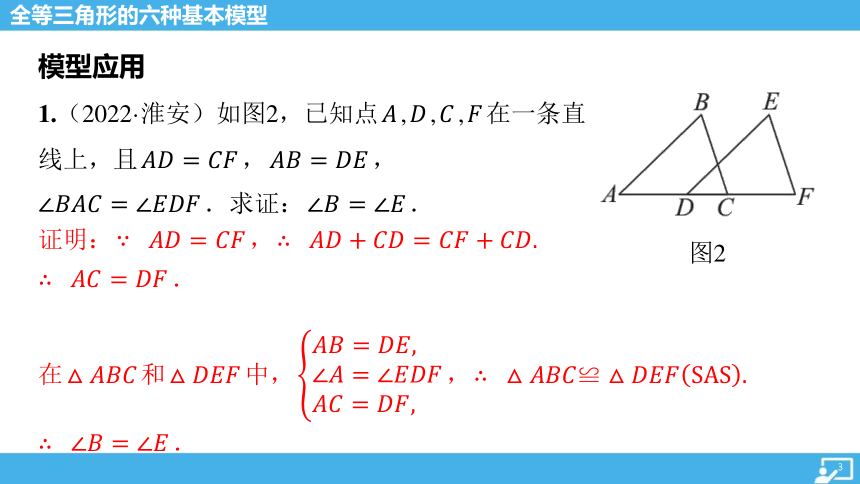
图2
1.(2022·淮安)如图2,已知点 , , , 在一条直
线上,且 , ,
.求证: .
证明: ,
.
在 和 中, ,
.
图3
2.如图3,已知点 , , , 在同一条直线上,
, , .求证: .
证明: , ,即AB=CD.
, .
在 和 中, , , ,
.
模型二 对称型
模型剖析
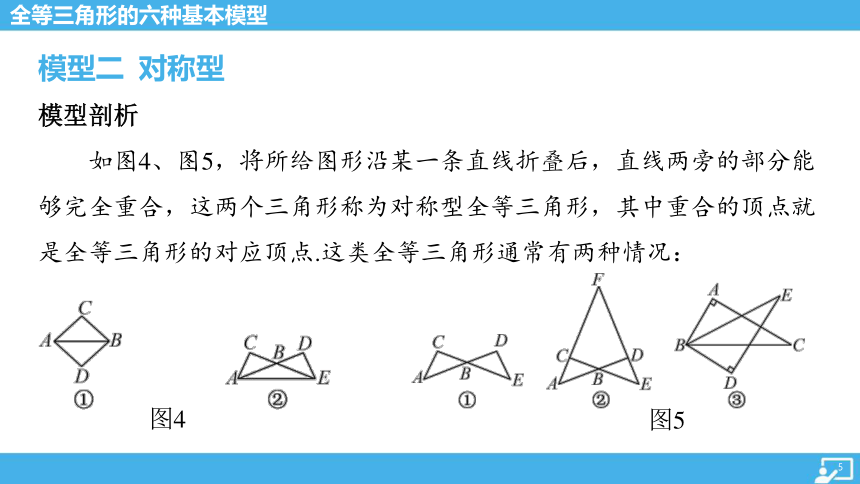
如图4、图5,将所给图形沿某一条直线折叠后,直线两旁的部分能
够完全重合,这两个三角形称为对称型全等三角形,其中重合的顶点就
是全等三角形的对应顶点.这类全等三角形通常有两种情况:
图4
图5
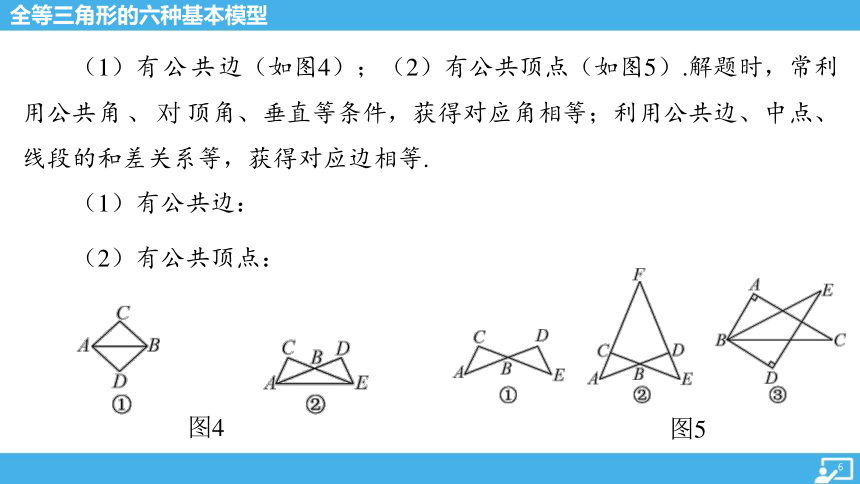
(1)有公共边(如图4);(2)有公共顶点(如图5).解题时,常利用公共角、对顶角、垂直等条件,获得对应角相等;利用公共边、中点、线段的和差关系等,获得对应边相等.
(1)有公共边:
图4
(2)有公共顶点:
图5
模型应用
图6
3.(2022·兰州)小军制作的燕子风筝骨架图如图6
所示, , , ,
,求 的度数.
解: ,
,即 .
在 和 中,
.
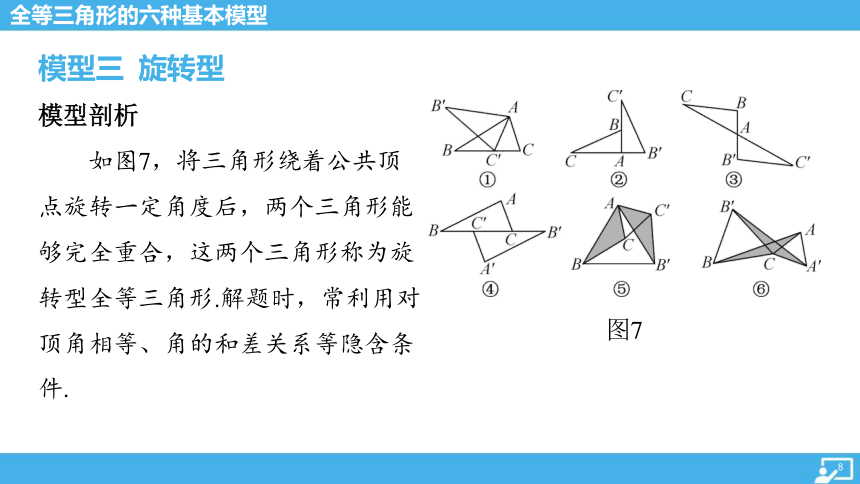
模型三 旋转型
图7
模型剖析
如图7,将三角形绕着公共顶
点旋转一定角度后,两个三角形能
够完全重合,这两个三角形称为旋
转型全等三角形.解题时,常利用对
顶角相等、角的和差关系等隐含条
件.
模型应用
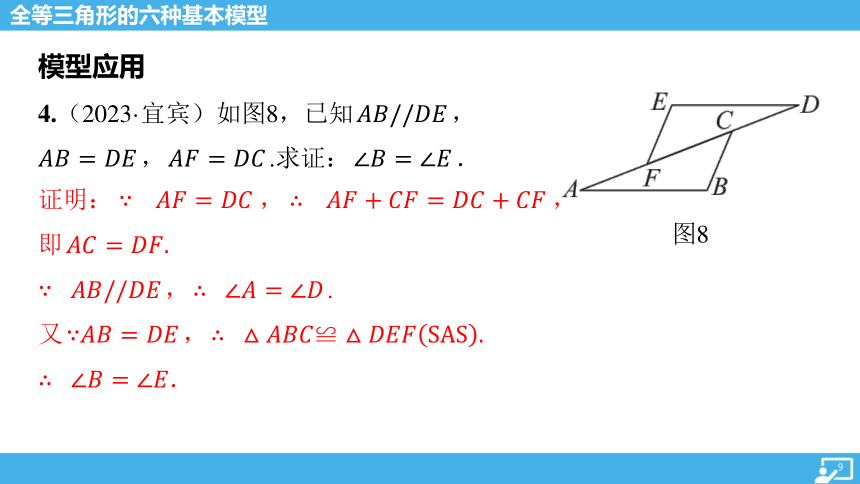
图8
4.(2023·宜宾)如图8,已知 ,
, .求证: .
证明: , ,
即
, .
又 ,
图9
5.(2023·陕西)如图9,在 中, ,
.过点 作 ,垂足为点 ,延长
至点 ,使 .在边 上截取 ,连
接 .求证: .
图9
证明:在 中, , ,
.
, .
.
.
在 和 中, ,
.
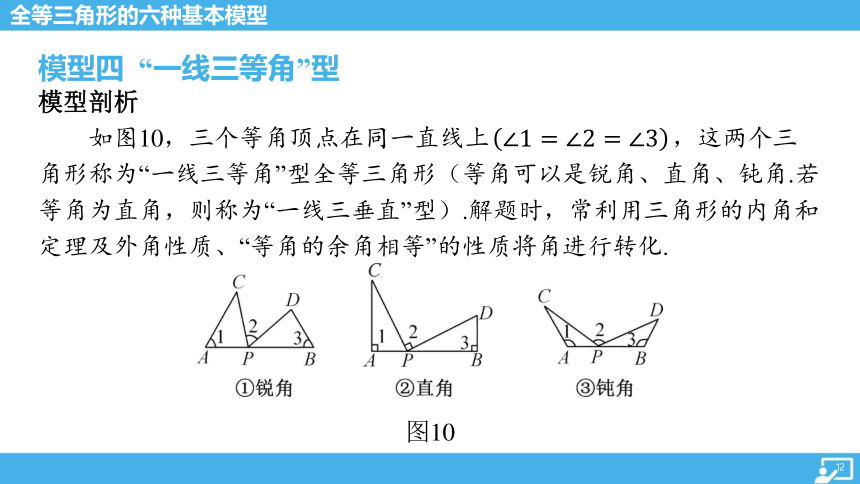
模型四 “一线三等角”型
模型剖析
如图10,三个等角顶点在同一直线上 ,这两个三
角形称为“一线三等角”型全等三角形(等角可以是锐角、直角、钝角.若
等角为直角,则称为“一线三垂直”型).解题时,常利用三角形的内角和
定理及外角性质、“等角的余角相等”的性质将角进行转化.
图10
【拓展】“一线三垂直”型
一线:如图11,经过直角顶点的直线 ;
三垂直:直角三角形的两边互相垂直 ,过直角三角形的
两边上一点分别向直线作垂线 ,利用“同角的余角
相等”找等角 .
图11
模型应用
图12
6.(2022·铜仁)如图12,点 在 上,
, , , .求
证: .
图12
证明: , , ,
.
, .
.在 和 中,
.
图13
7.(2023·聊城)如图13,在四边形 中,点
是边 上一点,且 ,
.
(1)求证: .
证明: , ,
.
在 和 中,
.
图13
(2)若 , 时,求 的面积.
解: , ,
为等边三角形.
.
过点 作 于点 ,
.
.
模型五 半角模型
模型剖析
当一个角包含着这个角的半角时,常将半角两边的三角形通过旋转
到一边合并形成新的三角形,从而进行等量代换,然后证明与半角形成
的三角形全等,从而得到线段或角之间的数量关系.半角模型常有如下
三种类型.
1.等边三角形含半角(如图14, , )
图14
结论: , .
2.等腰直角三角形含半角(如图15, , )
图15
结论: , .
3.正方形含半角(如图16)
图16
结论: , .
模型应用
图17
8.如图17, 是边长为1的等边三角形, ,
,点 , 分别在 , 上,且
.求 的周长.
提示:如图16,延长 至点 ,使 ,连接
是等边三角形, . , , . . .在
和 中, , ,
, ,
图16
图16
, , . . .在 和 中, , , , 的周长 .
【答案】2
模型六 对角互补模型
模型剖析
对角互补模型,即四边形构成的几何图形中,相对的角互补.解决
此类题型常用到的辅助线画法主要有两种:(1)过顶点作两垂线;(2)
旋转法.
对角互补模型常有如下两种类型.
1.含 角的对角互补模型
如图18, , 平分 .
图18
作法1:分别过点 作 , 的垂线.
作法2:将 绕点 逆时针旋转 得到 .
结论:图中两个阴影三角形全等.
2.含 角的对角互补模型
如图19, , 平分 .
图19
作法1:分别过点 作 , 的垂线.
作法2:将 绕点 逆时针旋转 得到 .
结论:图中两个阴影三角形全等.
模型应用
图20
9.如图20,在四边形 中, , ,
,求四边形 的面积.
图17
解:如图17,过点 作 ,交 的延长线于点 .
因为 ,所以 .
又 ,所以 .
又因为 ,所以 .
在 和 中,因为 , , ,所以 .
图17
所以 ,即 是等腰直角三角形.
所以 .
因为 ,所以四边形 的面积为 .
微专题练习(四)
全等三角形的六种基本模型
模型一 平移型
图1
1.(2022·宜宾)如图1,已知点 , , , 在
同一直线上, , ,
.求证: .
图1
证明: , .
在 和 中,
,即 .
模型二 对称型
图2
2.(2023·云南)如图2, 是 的中点,
, .求证: .
证明: 是 的中点, .
在 和 中,
.
模型三 旋转型
图3
3.如图3, , , , .
(1)求证: .
证明: , , .
.
在 和 中, , ,
,
(2)求证: .
图3
图21
解:如图21,设 交 于点 , 交 于点
, .
又 , , .
.
.
模型四 “一线三等角”型
图4
4.(2021·南充)如图4, , 是 内
部一条射线.若 , 于点 , 于
点 .求证: .
证明: , .
, , .
. .
在 和 中, , , ,
.
模型五 半角模型
图5
5.如图5,在平面直角坐标系中, 轴于点 ,
轴于点 ,点 , .过点 作 分别
交线段 , 于点 , .
(1)当 时,求证: .
证明: 轴, 轴, .
又 , 四边形 是矩形.
.
, ,
四边形 是正方形.
, , .
在 和 中, , , ,
.
图5
(2)如图6,当 , 时,求 的值.
图6
解:如图22,将 绕点 顺时针旋转 ,得到
,则 ,
, .
.
.在 和 中, , , ,
,
.
图22
图22
由(1)知四边形 是边长为4的正方形,
.
模型六 对角互补模型
图7
6.如图7,在菱形 中, ,点
, 分别在边 , 上, .请判
断 的形状,并给出证明.
解: 是等边三角形.证明如下:如图23,连接
四边形 是菱形,, , , .
是等边三角 形.
图23
图23
, ,
.
又 , .
在 和 中, , , ,
.
又 , 是等边三角形.
微专题 全等三角形的六种基本模型
模型一 平移型
模型剖析
如图1,把 沿直线 平移,所得 与 称为平移型
全等三角形.解题时,常利用平行线的性质,获得对应角相等;利用在
平移方向上相等的线段加(减)公共线段的方法,获得对应边相等.
图1
模型应用
图2
1.(2022·淮安)如图2,已知点 , , , 在一条直
线上,且 , ,
.求证: .
证明: ,
.
在 和 中, ,
.
图3
2.如图3,已知点 , , , 在同一条直线上,
, , .求证: .
证明: , ,即AB=CD.
, .
在 和 中, , , ,
.
模型二 对称型
模型剖析
如图4、图5,将所给图形沿某一条直线折叠后,直线两旁的部分能
够完全重合,这两个三角形称为对称型全等三角形,其中重合的顶点就
是全等三角形的对应顶点.这类全等三角形通常有两种情况:
图4
图5
(1)有公共边(如图4);(2)有公共顶点(如图5).解题时,常利用公共角、对顶角、垂直等条件,获得对应角相等;利用公共边、中点、线段的和差关系等,获得对应边相等.
(1)有公共边:
图4
(2)有公共顶点:
图5
模型应用
图6
3.(2022·兰州)小军制作的燕子风筝骨架图如图6
所示, , , ,
,求 的度数.
解: ,
,即 .
在 和 中,
.
模型三 旋转型
图7
模型剖析
如图7,将三角形绕着公共顶
点旋转一定角度后,两个三角形能
够完全重合,这两个三角形称为旋
转型全等三角形.解题时,常利用对
顶角相等、角的和差关系等隐含条
件.
模型应用
图8
4.(2023·宜宾)如图8,已知 ,
, .求证: .
证明: , ,
即
, .
又 ,
图9
5.(2023·陕西)如图9,在 中, ,
.过点 作 ,垂足为点 ,延长
至点 ,使 .在边 上截取 ,连
接 .求证: .
图9
证明:在 中, , ,
.
, .
.
.
在 和 中, ,
.
模型四 “一线三等角”型
模型剖析
如图10,三个等角顶点在同一直线上 ,这两个三
角形称为“一线三等角”型全等三角形(等角可以是锐角、直角、钝角.若
等角为直角,则称为“一线三垂直”型).解题时,常利用三角形的内角和
定理及外角性质、“等角的余角相等”的性质将角进行转化.
图10
【拓展】“一线三垂直”型
一线:如图11,经过直角顶点的直线 ;
三垂直:直角三角形的两边互相垂直 ,过直角三角形的
两边上一点分别向直线作垂线 ,利用“同角的余角
相等”找等角 .
图11
模型应用
图12
6.(2022·铜仁)如图12,点 在 上,
, , , .求
证: .
图12
证明: , , ,
.
, .
.在 和 中,
.
图13
7.(2023·聊城)如图13,在四边形 中,点
是边 上一点,且 ,
.
(1)求证: .
证明: , ,
.
在 和 中,
.
图13
(2)若 , 时,求 的面积.
解: , ,
为等边三角形.
.
过点 作 于点 ,
.
.
模型五 半角模型
模型剖析
当一个角包含着这个角的半角时,常将半角两边的三角形通过旋转
到一边合并形成新的三角形,从而进行等量代换,然后证明与半角形成
的三角形全等,从而得到线段或角之间的数量关系.半角模型常有如下
三种类型.
1.等边三角形含半角(如图14, , )
图14
结论: , .
2.等腰直角三角形含半角(如图15, , )
图15
结论: , .
3.正方形含半角(如图16)
图16
结论: , .
模型应用
图17
8.如图17, 是边长为1的等边三角形, ,
,点 , 分别在 , 上,且
.求 的周长.
提示:如图16,延长 至点 ,使 ,连接
是等边三角形, . , , . . .在
和 中, , ,
, ,
图16
图16
, , . . .在 和 中, , , , 的周长 .
【答案】2
模型六 对角互补模型
模型剖析
对角互补模型,即四边形构成的几何图形中,相对的角互补.解决
此类题型常用到的辅助线画法主要有两种:(1)过顶点作两垂线;(2)
旋转法.
对角互补模型常有如下两种类型.
1.含 角的对角互补模型
如图18, , 平分 .
图18
作法1:分别过点 作 , 的垂线.
作法2:将 绕点 逆时针旋转 得到 .
结论:图中两个阴影三角形全等.
2.含 角的对角互补模型
如图19, , 平分 .
图19
作法1:分别过点 作 , 的垂线.
作法2:将 绕点 逆时针旋转 得到 .
结论:图中两个阴影三角形全等.
模型应用
图20
9.如图20,在四边形 中, , ,
,求四边形 的面积.
图17
解:如图17,过点 作 ,交 的延长线于点 .
因为 ,所以 .
又 ,所以 .
又因为 ,所以 .
在 和 中,因为 , , ,所以 .
图17
所以 ,即 是等腰直角三角形.
所以 .
因为 ,所以四边形 的面积为 .
微专题练习(四)
全等三角形的六种基本模型
模型一 平移型
图1
1.(2022·宜宾)如图1,已知点 , , , 在
同一直线上, , ,
.求证: .
图1
证明: , .
在 和 中,
,即 .
模型二 对称型
图2
2.(2023·云南)如图2, 是 的中点,
, .求证: .
证明: 是 的中点, .
在 和 中,
.
模型三 旋转型
图3
3.如图3, , , , .
(1)求证: .
证明: , , .
.
在 和 中, , ,
,
(2)求证: .
图3
图21
解:如图21,设 交 于点 , 交 于点
, .
又 , , .
.
.
模型四 “一线三等角”型
图4
4.(2021·南充)如图4, , 是 内
部一条射线.若 , 于点 , 于
点 .求证: .
证明: , .
, , .
. .
在 和 中, , , ,
.
模型五 半角模型
图5
5.如图5,在平面直角坐标系中, 轴于点 ,
轴于点 ,点 , .过点 作 分别
交线段 , 于点 , .
(1)当 时,求证: .
证明: 轴, 轴, .
又 , 四边形 是矩形.
.
, ,
四边形 是正方形.
, , .
在 和 中, , , ,
.
图5
(2)如图6,当 , 时,求 的值.
图6
解:如图22,将 绕点 顺时针旋转 ,得到
,则 ,
, .
.
.在 和 中, , , ,
,
.
图22
图22
由(1)知四边形 是边长为4的正方形,
.
模型六 对角互补模型
图7
6.如图7,在菱形 中, ,点
, 分别在边 , 上, .请判
断 的形状,并给出证明.
解: 是等边三角形.证明如下:如图23,连接
四边形 是菱形,, , , .
是等边三角 形.
图23
图23
, ,
.
又 , .
在 和 中, , , ,
.
又 , 是等边三角形.
同课章节目录
