微专题 相似三角形的四种基本模型- 2024年中考数学复习课件(共29张PPT)
文档属性
| 名称 | 微专题 相似三角形的四种基本模型- 2024年中考数学复习课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 21:47:33 | ||
图片预览





文档简介
(共29张PPT)
微专题 相似三角形的四种基本模型
模型一 “ ”型
图1
模型剖析
“ ”字模型:如图1,有一组隐含的等角
(对顶角) .此时只要再设法证明另一
组角相等或等角的两边对应成比例,就
可证得两个三角形相似.若题中未明确相
似三角形的对应顶点,则需要分类讨论.
结论: ;
.
模型应用
图2
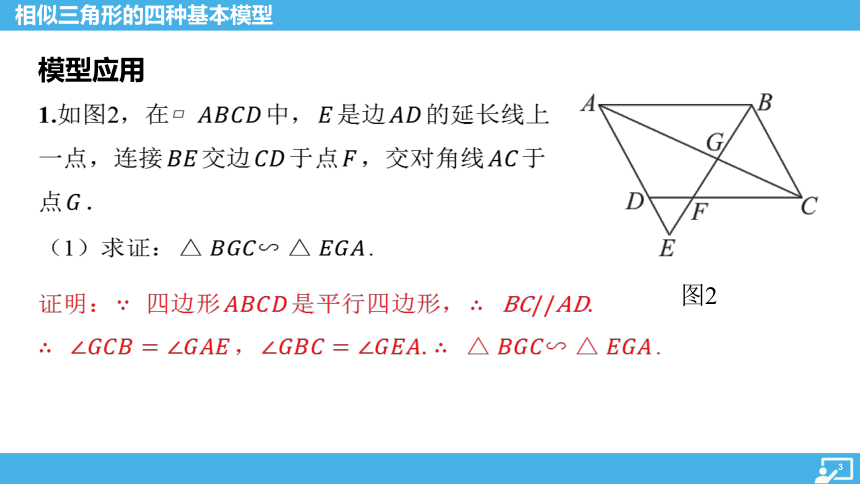
1.如图2,在 中, 是边 的延长线上一点,连接 交边 于点 ,交对角线 于点 .
(1)求证: .
证明: 四边形 是平行四边形,
, .
图2
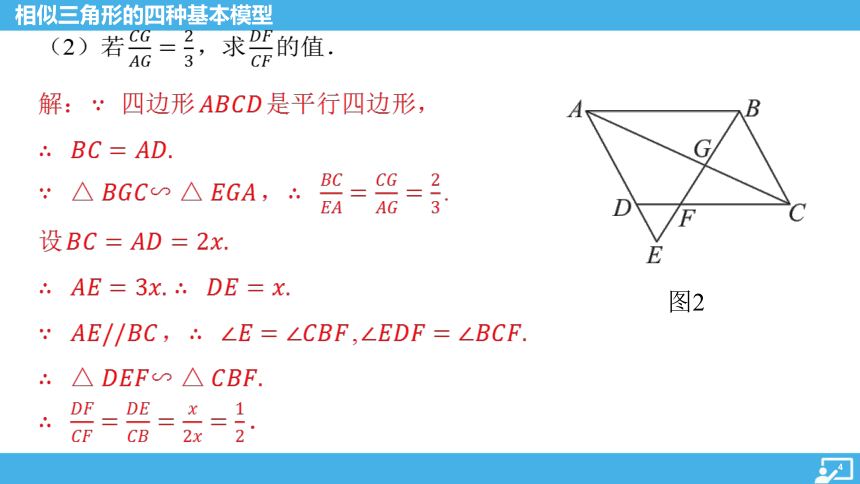
(2)若 ,求 的值.
解: 四边形 是平行四边形,
, .
设
, ,
.
模型二 “ ”型
图3
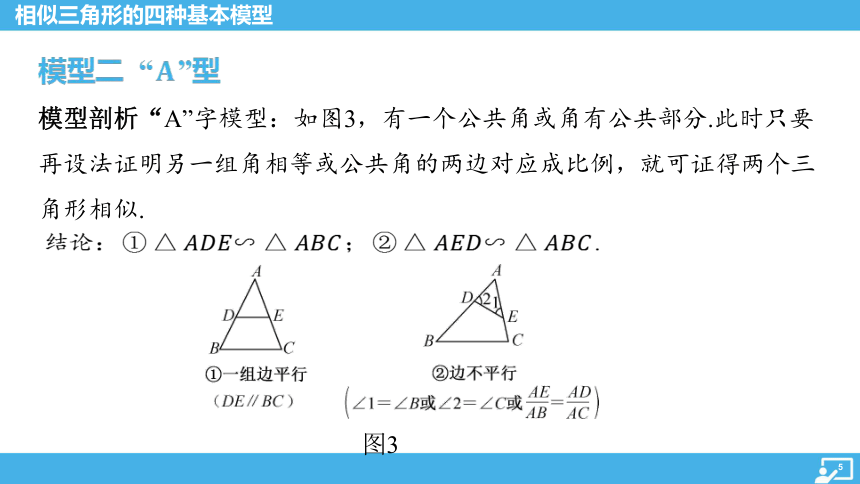
模型剖析“A”字模型:如图3,有一个公共角或角有公共部分.此时只要再设法证明另一组角相等或公共角的两边对应成比例,就可证得两个三角形相似.
结论: ; .
模型应用
图4
2.(2022·杭州)如图4,在 中,点 , ,
分别在边 , , 上,连接 , .已
知四边形 是平行四边形, .
(1)若 ,求线段 的长.
解: 四边形 是平行四边形,
.
又 , .
(2)若 的面积为1,求 的面积.
图4
解: , .
又 的面积为1, 的面积是
四边形 是平行四边形, ,
, .
.
.
图4
.
模型三 “母子”型
模型剖析
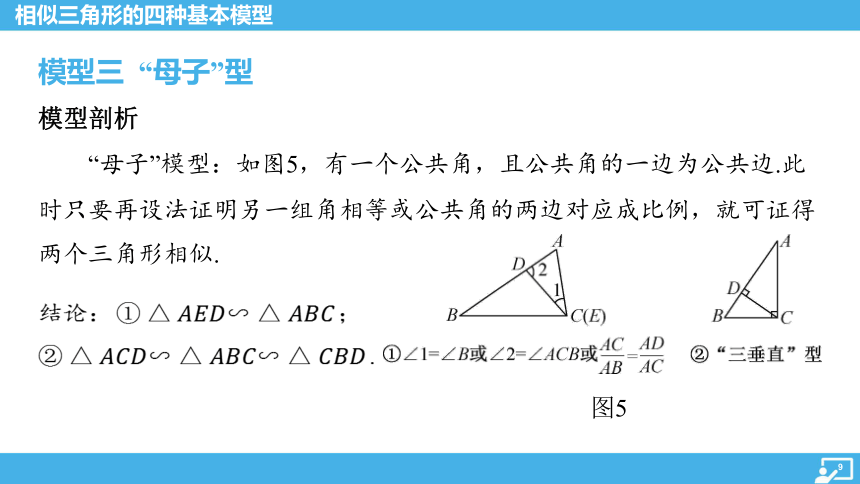
“母子”模型:如图5,有一个公共角,且公共角的一边为公共边.此
时只要再设法证明另一组角相等或公共角的两边对应成比例,就可证得
两个三角形相似.
图5
结论: ;
.
【拓展】“三垂直”型
如图6,直角三角形被斜边上的高分成的两个直角三角形与原三角
形相似,即 .
图6
常见的结论有: , , .
模型应用
图7
3.(2022·贵阳)如图7,在 中, 是 边
上的点, , ,则 与 的周长比是( ) .
B
A. B. C. D.
图8
4.(2021·南充 改编)如图8,在 中, 为 上一
点, ,求 的值.
解: , .
又 ,
.
.
图9
5.如图9,在 中, ,
于点 , 为线段 上一点,且 ,过点
作 交 于点 ,则线段 , ,
满足什么数量关系?
解: , ,
.
.
.
又 ,
.
.
图9
, , ,
.
.
, .
又 ,
.
模型四 “一线三等角”型
模型剖析
“一线三等角”模型:如图10,点 在直线 上,
(无论是锐角、直角,还是钝角),则
.“一线三等角”型图形证相似,通常利用三角形内角和定理、邻补
角的性质、平角的性质等证两组角对应相等.
图10
【拓展】“一线三垂直”型
“一线三垂直”模型:如图11,点 在直线 上,
,则 .
图11
模型应用
图12
6.如图12,在四边形 中, , , , 为 上一,且 .若 , ,则 的长为___.
提示: , ,
. , . , .
. , , , .又 , .
图13
7.(2023·邵阳)如图13, , ,点
是线段 上的一点,且 .已知
, , .
(1)求证: .
证明: , , ,
.
, .
.
(2)求线段 的长.
解: , .
.
图13
图14
8.如图14,在 中, , , 分别是 ,
边上的点,且 .
(1)求证: .
证明: , .
又 ,
, ,
.
.
又 , .
图14
(2)若 , ,当 时,求 的长.
解: , .
又 , .
又 ,
.
, , .
.
微专题练习(七)
相似三角形的四种基本模型
模型一 “ ”型
图1
1.(2022·泰安 节选)如图1,在矩形 中,
点 在 上, , 与 相交于点
, 与 相交于点 .找出图中与 相似的三角形,并说明理由.
图39
解:与 相似的三角形有 , .
理由如下:如图39,
,
,
.
又 ,
,
.
又 , .
模型二 “A”型
图2
2.如图2,在平面直角坐标系中,已知
, .点 从点 开始沿
向点 以 的速度移动,点 从点 开始沿
向点 以 的速度移动.当一点运动到终
点时,另一点也随之停止.如果 , 同时出发,
用 表示移动的时间 ,当以点 , , 为顶点的三角形
与以点 , , 为顶点的三角形相似时,求 的值.
图2
解:由题意知, , .
①若 ,则 ,即 ,解得 .
②若 ,则 ,即 ,解得 .
综上可知,当 或 时,以点 , , 为顶点的三角形与以点 , , 为顶点的三角形相似.
模型三 “母子”型
图3
3.如图3, 是 的边 上的一点, ,
, .
(1)求证: .
证明: , , , , .
.
又 , .
图3
(2)若 ,求 的长.
解: , .
, ,即 .
.
模型四 “一线三等角”型
图4
4.如图4, 与 均为等腰三角形,
, .点 在边 上,且
,点 为 与 的交点.
(1)求证: .
证明: , ,
与 均为等腰三角形, , , . .
图4
(2)求证: .
证明: ,
.
又 ,
,即 .
又 ,
,即 .
微专题 相似三角形的四种基本模型
模型一 “ ”型
图1
模型剖析
“ ”字模型:如图1,有一组隐含的等角
(对顶角) .此时只要再设法证明另一
组角相等或等角的两边对应成比例,就
可证得两个三角形相似.若题中未明确相
似三角形的对应顶点,则需要分类讨论.
结论: ;
.
模型应用
图2
1.如图2,在 中, 是边 的延长线上一点,连接 交边 于点 ,交对角线 于点 .
(1)求证: .
证明: 四边形 是平行四边形,
, .
图2
(2)若 ,求 的值.
解: 四边形 是平行四边形,
, .
设
, ,
.
模型二 “ ”型
图3
模型剖析“A”字模型:如图3,有一个公共角或角有公共部分.此时只要再设法证明另一组角相等或公共角的两边对应成比例,就可证得两个三角形相似.
结论: ; .
模型应用
图4
2.(2022·杭州)如图4,在 中,点 , ,
分别在边 , , 上,连接 , .已
知四边形 是平行四边形, .
(1)若 ,求线段 的长.
解: 四边形 是平行四边形,
.
又 , .
(2)若 的面积为1,求 的面积.
图4
解: , .
又 的面积为1, 的面积是
四边形 是平行四边形, ,
, .
.
.
图4
.
模型三 “母子”型
模型剖析
“母子”模型:如图5,有一个公共角,且公共角的一边为公共边.此
时只要再设法证明另一组角相等或公共角的两边对应成比例,就可证得
两个三角形相似.
图5
结论: ;
.
【拓展】“三垂直”型
如图6,直角三角形被斜边上的高分成的两个直角三角形与原三角
形相似,即 .
图6
常见的结论有: , , .
模型应用
图7
3.(2022·贵阳)如图7,在 中, 是 边
上的点, , ,则 与 的周长比是( ) .
B
A. B. C. D.
图8
4.(2021·南充 改编)如图8,在 中, 为 上一
点, ,求 的值.
解: , .
又 ,
.
.
图9
5.如图9,在 中, ,
于点 , 为线段 上一点,且 ,过点
作 交 于点 ,则线段 , ,
满足什么数量关系?
解: , ,
.
.
.
又 ,
.
.
图9
, , ,
.
.
, .
又 ,
.
模型四 “一线三等角”型
模型剖析
“一线三等角”模型:如图10,点 在直线 上,
(无论是锐角、直角,还是钝角),则
.“一线三等角”型图形证相似,通常利用三角形内角和定理、邻补
角的性质、平角的性质等证两组角对应相等.
图10
【拓展】“一线三垂直”型
“一线三垂直”模型:如图11,点 在直线 上,
,则 .
图11
模型应用
图12
6.如图12,在四边形 中, , , , 为 上一,且 .若 , ,则 的长为___.
提示: , ,
. , . , .
. , , , .又 , .
图13
7.(2023·邵阳)如图13, , ,点
是线段 上的一点,且 .已知
, , .
(1)求证: .
证明: , , ,
.
, .
.
(2)求线段 的长.
解: , .
.
图13
图14
8.如图14,在 中, , , 分别是 ,
边上的点,且 .
(1)求证: .
证明: , .
又 ,
, ,
.
.
又 , .
图14
(2)若 , ,当 时,求 的长.
解: , .
又 , .
又 ,
.
, , .
.
微专题练习(七)
相似三角形的四种基本模型
模型一 “ ”型
图1
1.(2022·泰安 节选)如图1,在矩形 中,
点 在 上, , 与 相交于点
, 与 相交于点 .找出图中与 相似的三角形,并说明理由.
图39
解:与 相似的三角形有 , .
理由如下:如图39,
,
,
.
又 ,
,
.
又 , .
模型二 “A”型
图2
2.如图2,在平面直角坐标系中,已知
, .点 从点 开始沿
向点 以 的速度移动,点 从点 开始沿
向点 以 的速度移动.当一点运动到终
点时,另一点也随之停止.如果 , 同时出发,
用 表示移动的时间 ,当以点 , , 为顶点的三角形
与以点 , , 为顶点的三角形相似时,求 的值.
图2
解:由题意知, , .
①若 ,则 ,即 ,解得 .
②若 ,则 ,即 ,解得 .
综上可知,当 或 时,以点 , , 为顶点的三角形与以点 , , 为顶点的三角形相似.
模型三 “母子”型
图3
3.如图3, 是 的边 上的一点, ,
, .
(1)求证: .
证明: , , , , .
.
又 , .
图3
(2)若 ,求 的长.
解: , .
, ,即 .
.
模型四 “一线三等角”型
图4
4.如图4, 与 均为等腰三角形,
, .点 在边 上,且
,点 为 与 的交点.
(1)求证: .
证明: , ,
与 均为等腰三角形, , , . .
图4
(2)求证: .
证明: ,
.
又 ,
,即 .
又 ,
,即 .
同课章节目录
