微专题 与圆的性质有关的计算与证明方法- 2024年中考数学复习课件(共20张PPT)
文档属性
| 名称 | 微专题 与圆的性质有关的计算与证明方法- 2024年中考数学复习课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 16:36:29 | ||
图片预览








文档简介
(共20张PPT)
与圆的性质有关的计算与证明方法
方法一 构造等腰三角形
方法解读
因为圆内半径相等,所以经常利用半径来构造等腰三角形,从而利
用等腰三角形的性质进行计算或证明.
方法应用
图1
1.(2023·巴中)如图1, 是 的外接圆.若
,则 的度数是( ) .
D
A. B. C. D.
图2
2.如图2, 为 的弦,半径 , 分别交 于点
, ,且 .求证: .
证明:连接 , ,
,
.
方法二 构造直角三角形
(1)利用直径构造直角三角形
方法解读
当已知圆的直径时,通常作直径所对的圆周角,利用圆周角的性质
得到直角三角形.反之,当圆中某个圆周角是直角时,它所对的弦是直
径,通常作这个圆周角所对的弦,得到直径.
方法应用
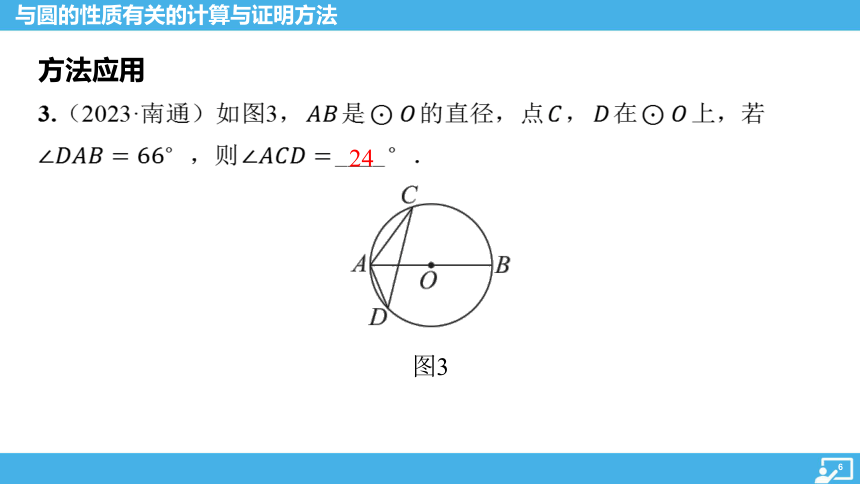
3.(2023·南通)如图3, 是 的直径,点 , 在 上,若
,则 ____ .
24
图3
图4
4.如图4, 经过平面直角坐标系的原点 ,交 轴
于点 ,交 轴于点 , 为第二象限内圆
上一点,则 的余弦值是( ) .
A. B. C. D.
图31
提示:如图31,连接 , 为
的直径. , , ,
.在 中,由勾股定理,得 .由圆周角定理的推论,得 , 的余弦值是 .
【答案】B
(2) 过圆心作弦的垂线段构造直角三角形
方法解读
在圆中,求弦长、半径或圆心到弦的距离时,常过圆心作弦的垂线段,
再连接半径构造直角三角形,从而利用勾股定理或锐角三角函数关系进
行计算.
方法应用
图5
5.(2021·柳州)往水平放置的半径为 的圆柱形容器
内装入一些水以后,截面图如图5所示.若水面宽度
,则水的最大深度为( ) .
A. B. C. D.
图32
提示:如图32,连接 ,过点 作 于点 ,交
于点 , 由垂径定理,得 在 中,由勾股定理,
得 .
【答案】B
6.(2023·广安)如图6, 内接于 , 的半径为7,
,则弦 的长为_____.
图6
图33
提示:如图33,作 于点 ,
连接 , , .又 , , , . .
【答案】
微专题练习(八)
与圆的性质有关的计算与证明方法
方法一 构造等腰三角形
图1
1.(2022·西藏)如图1, 是 的弦, ,垂足
为点 , , ,则 的度数为
( ) .
D
A. B. C. D.
图2
2.如图2, 是半圆 的直径, 是半圆上的一点,
, 交 的延长线于点 ,交半圆
于点 ,且 .求 的度数.
图62
解:如图62,连接
, ,
,
, .
.
方法二 构造直角三角形
图3
3.(2022·包头)如图3, , 是 的两条直径,
是 的中点,连接 , .若 ,则
的度数是( ) .
C
A. B. C. D.
图4
4.如图4,在 中, ,
,点 , 在 上,边 , 分别交
于点 , ,点 是 的中点,则 的度数
是( ) .
A
A. B. C. D.
图5
5.(2023·永州)如图5, 是一个盛有水的容器的横截
面, 的半径为 ,水的最深处到水面 的距离为
,则水面 的宽度为____ .
16
6.如图6, 的直径 和弦 相交于点 ,已知 ,
, .
图6
备用图
(1)求 的长.
图63
解:如图63,作 于 ,连接
, ,
半径 .
在 中, , ,
.
在 中,
, .
(2)当直线 绕点 顺时针旋转 ,交 于点 , 时,请直接
写出弦 的长.
图64
提示:如图64,作 于点 ,连接 .由(1)
知, . 直线 绕点 顺时针旋转 ,
.在 中,
, ,
.在 中,
, .
【答案】
与圆的性质有关的计算与证明方法
方法一 构造等腰三角形
方法解读
因为圆内半径相等,所以经常利用半径来构造等腰三角形,从而利
用等腰三角形的性质进行计算或证明.
方法应用
图1
1.(2023·巴中)如图1, 是 的外接圆.若
,则 的度数是( ) .
D
A. B. C. D.
图2
2.如图2, 为 的弦,半径 , 分别交 于点
, ,且 .求证: .
证明:连接 , ,
,
.
方法二 构造直角三角形
(1)利用直径构造直角三角形
方法解读
当已知圆的直径时,通常作直径所对的圆周角,利用圆周角的性质
得到直角三角形.反之,当圆中某个圆周角是直角时,它所对的弦是直
径,通常作这个圆周角所对的弦,得到直径.
方法应用
3.(2023·南通)如图3, 是 的直径,点 , 在 上,若
,则 ____ .
24
图3
图4
4.如图4, 经过平面直角坐标系的原点 ,交 轴
于点 ,交 轴于点 , 为第二象限内圆
上一点,则 的余弦值是( ) .
A. B. C. D.
图31
提示:如图31,连接 , 为
的直径. , , ,
.在 中,由勾股定理,得 .由圆周角定理的推论,得 , 的余弦值是 .
【答案】B
(2) 过圆心作弦的垂线段构造直角三角形
方法解读
在圆中,求弦长、半径或圆心到弦的距离时,常过圆心作弦的垂线段,
再连接半径构造直角三角形,从而利用勾股定理或锐角三角函数关系进
行计算.
方法应用
图5
5.(2021·柳州)往水平放置的半径为 的圆柱形容器
内装入一些水以后,截面图如图5所示.若水面宽度
,则水的最大深度为( ) .
A. B. C. D.
图32
提示:如图32,连接 ,过点 作 于点 ,交
于点 , 由垂径定理,得 在 中,由勾股定理,
得 .
【答案】B
6.(2023·广安)如图6, 内接于 , 的半径为7,
,则弦 的长为_____.
图6
图33
提示:如图33,作 于点 ,
连接 , , .又 , , , . .
【答案】
微专题练习(八)
与圆的性质有关的计算与证明方法
方法一 构造等腰三角形
图1
1.(2022·西藏)如图1, 是 的弦, ,垂足
为点 , , ,则 的度数为
( ) .
D
A. B. C. D.
图2
2.如图2, 是半圆 的直径, 是半圆上的一点,
, 交 的延长线于点 ,交半圆
于点 ,且 .求 的度数.
图62
解:如图62,连接
, ,
,
, .
.
方法二 构造直角三角形
图3
3.(2022·包头)如图3, , 是 的两条直径,
是 的中点,连接 , .若 ,则
的度数是( ) .
C
A. B. C. D.
图4
4.如图4,在 中, ,
,点 , 在 上,边 , 分别交
于点 , ,点 是 的中点,则 的度数
是( ) .
A
A. B. C. D.
图5
5.(2023·永州)如图5, 是一个盛有水的容器的横截
面, 的半径为 ,水的最深处到水面 的距离为
,则水面 的宽度为____ .
16
6.如图6, 的直径 和弦 相交于点 ,已知 ,
, .
图6
备用图
(1)求 的长.
图63
解:如图63,作 于 ,连接
, ,
半径 .
在 中, , ,
.
在 中,
, .
(2)当直线 绕点 顺时针旋转 ,交 于点 , 时,请直接
写出弦 的长.
图64
提示:如图64,作 于点 ,连接 .由(1)
知, . 直线 绕点 顺时针旋转 ,
.在 中,
, ,
.在 中,
, .
【答案】
同课章节目录
