微专题 与切线性质有关的计算问题 -2024年中考数学复习课件(共30张PPT)
文档属性
| 名称 | 微专题 与切线性质有关的计算问题 -2024年中考数学复习课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
与切线性质有关的计算问题
类型一 切线与锐角三角函数的计算问题
方法解读 解决切线与锐角三角函数的计算问题,通常借助圆的切线垂
直于过切点的半径的性质得到直角三角形.在直角三角形中,利用直角
三角形的性质或锐角三角函数等相关知识求边或角
方法应用
图1
1.如图1,在 中, , 为 的切线,点
, 分别为切点,线段 经过圆心 且与 相交
于 , 两点.若 , ,则 的长为
_____.
图43
提示:如图43,连接 , 分别切 于点
, , , .设 的半径为 ,
则 .在 中,
, . .
, .解得
,
.在 中, ,
.
【答案】
类型二 切线与勾股定理的计算问题
方法解读 解决切线与勾股定理的计算问题,通常利用切线的性质构造
直角三角形,然后利用勾股定理,建立线段之间的关系,从而为解决问
题提供突破口.
方法应用
图2
2.(2023·南宁一模)如图2,以点 为圆心的两个同心圆
中,大圆的弦 是小圆的切线, 为切点,大圆、小圆
的半径分别为5和3,则 的长为___.
图44
提示:如图44,连接 , 大圆的弦 是小圆的切
线, 为切点, .在
中, , ,
.
【答案】8
类型三 坐标系中关于切线的计算问题
方法解读 遇到圆与坐标轴相切,求点的坐标的问题时,通常将点的坐
标转化为线段的长,然后利用垂径定理和勾股定理求解.
方法应用
图3
3.如图3,在平面直角坐标系中, 与 轴相切,与
轴相交于点 , ,则圆心 的坐标是
( ) .
A. B. C. D.
图45
提示:如图45,过点 作 于点 ,作
轴于点 ,连接 .由 , ,得 .因
为 ,所以 ,则 .
因为 与 轴相切于点 ,所以 .
在 中,由勾股定理,得
.所以 .
【答案】D
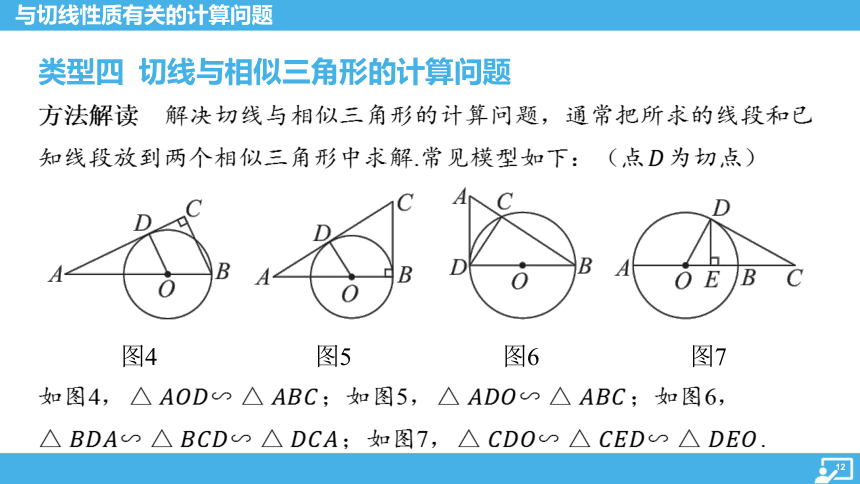
类型四 切线与相似三角形的计算问题
方法解读 解决切线与相似三角形的计算问题,通常把所求的线段和已
知线段放到两个相似三角形中求解.常见模型如下:(点 为切点)
图4
图5
图6
图7
如图4, ;如图5, ;如图6,
;如图7, .
方法应用
图8
4.(2021·贺州)如图8,在 中, ,
,点 在 上, .以 为半径的 与
相切于点 ,交 于点 ,则 的长为( ) .
A. B. C. D.1
图46
提示:如图46,连接 , .
因为 与 相切于点 , 是 的直径,所以
, .因为 ,即 ,所
以 , .所以 ,
,则 , .因为 ,
【答案】B
,所以 , , .因此
, .解得 , .所以 .
微专题练习(十)
与切线性质有关的计算问题
类型一 切线与锐角三角函数的计算问题
图1
1.如图1, 为 的直径,点 在 的延长线上,
, 与 相切,切点分别为点 , .若
, ,则 等于( ) .
A. B. C. D.
图72
提示:如图72,连接 , , , 交 于点 .
因为 , 与 分别相切于点 , ,所以
, , 平分 .所以 ,
则 .所以 .因为 ,
【答案】D
所以 .在 中,
,所以 .因此
.
图2
2.如图2,已知 是 的直径, 与 相切于点 ,
连接 , .若 ,则 ___.
提示:因为 与 相切于点 ,所以 ,则 .在
中, ,因此设 ,则 由勾股
定理知, ,则
.所以 .
类型二 切线与勾股定理的计算问题
图3
3.(2023·重庆A卷)如图3, 是 的切线,
为切点,连接 , .若 ,
, ,则 的长是( ) .
A.3 B. C. D.6
图73
提示:如图73,连接 是 的切线,
.
, , , .
【答案】C
图4
4.(2022·宁波)如图4,在 中, ,
,点 在 上.以 为半径的圆与 相切于
点 , 是 边上的动点.当 为直角三角形
时, 的长为______.
图74
提示:如图74,连接 .
与 相切于点 , .由题意知,点
的位置分如下两种情况.①当 时,点
与点 重合,设 的半径 ,则 ,
.在 中,由勾股定理,得
,即 .解得 ,即
当 时, ,如图74,由
,得 . , ,
, .综上所述, 的长为 或 .
【答案】 或
类型三 坐标系中关于切线的计算问题
图5
5.(2021·河池)如图5,在平面直角坐标系中,以点
为圆心、 长为直径的圆与 轴相切,与 轴交
于 , 两点,则点 的坐标是___________.
图75
提示:如图75,
设以 为直径的圆与 轴相切于点 ,连接 , ,
交于点 ,则 轴, ,即 ,
则 轴.所以 .因为 ,所以
, ,则 .
在 中,由勾股定理,得
【答案】
.所以 .所
以 .
图6
6.如图6,在平面直角坐标系中,点 在第一象限,
与 轴、 轴都相切,且经过矩形 的顶点 ,与
相交于点 .若 的半径为5,点 的坐标是 ,
则点 的坐标是______.
图76
提示:如图76,设 与 轴、 轴的切点分别为点
, ,连接 , , ,延长 与 交于点 ,
则 轴, 轴, .又 ,
所以四边形 是正方形,则 ,
.由 知, ,则
.易知四边形 和四边形 是矩形,则
, , .在 中,因为 弦 ,
所以 , .所以 .
在 中,由勾股定理,得 .所
以 .所以 .
【答案】
类型四 切线与相似三角形的计算问题
图7
7.(2021·荆州)如图7, 是 的直径, 是 的
弦, 于点 ,连接 ,过点 作 交
于点 ,过点 的切线交 的延长线于点 .若 ,
,则 ___.
图7
提示: , , 为
的中点, 为 的中位线. .在
中,
是 的切线, ,即 .
【答案】
, .又 ,
,即 .解得 .
图8
8.(2020·梧州 改编)如图8,在矩形 中,
, ,点 在对角线 上,以 为
半径作 交 于点 ,连接 .若 是 的
切线,则此时 的半径为___.
小锦囊 由切线的性质知, , 是 的半径,因此求
出 即可.又 ,因此作 于点 ,可得
,就可根据相似三角形的对应边成比例列方程求解.
图77
提示:如图77,过点 作 于点 .
因为四边形 是矩形,所以 ,
, .在 中,
.因为
,所以设 ,
,则 .因为 , ,
所以 ,则 .因为 是 的切线,
所以 ,则 .又因为 ,
所以 .又因为 ,所以
,则 ,即 .解得 (舍去)或
.所以 .
【答案】
与切线性质有关的计算问题
类型一 切线与锐角三角函数的计算问题
方法解读 解决切线与锐角三角函数的计算问题,通常借助圆的切线垂
直于过切点的半径的性质得到直角三角形.在直角三角形中,利用直角
三角形的性质或锐角三角函数等相关知识求边或角
方法应用
图1
1.如图1,在 中, , 为 的切线,点
, 分别为切点,线段 经过圆心 且与 相交
于 , 两点.若 , ,则 的长为
_____.
图43
提示:如图43,连接 , 分别切 于点
, , , .设 的半径为 ,
则 .在 中,
, . .
, .解得
,
.在 中, ,
.
【答案】
类型二 切线与勾股定理的计算问题
方法解读 解决切线与勾股定理的计算问题,通常利用切线的性质构造
直角三角形,然后利用勾股定理,建立线段之间的关系,从而为解决问
题提供突破口.
方法应用
图2
2.(2023·南宁一模)如图2,以点 为圆心的两个同心圆
中,大圆的弦 是小圆的切线, 为切点,大圆、小圆
的半径分别为5和3,则 的长为___.
图44
提示:如图44,连接 , 大圆的弦 是小圆的切
线, 为切点, .在
中, , ,
.
【答案】8
类型三 坐标系中关于切线的计算问题
方法解读 遇到圆与坐标轴相切,求点的坐标的问题时,通常将点的坐
标转化为线段的长,然后利用垂径定理和勾股定理求解.
方法应用
图3
3.如图3,在平面直角坐标系中, 与 轴相切,与
轴相交于点 , ,则圆心 的坐标是
( ) .
A. B. C. D.
图45
提示:如图45,过点 作 于点 ,作
轴于点 ,连接 .由 , ,得 .因
为 ,所以 ,则 .
因为 与 轴相切于点 ,所以 .
在 中,由勾股定理,得
.所以 .
【答案】D
类型四 切线与相似三角形的计算问题
方法解读 解决切线与相似三角形的计算问题,通常把所求的线段和已
知线段放到两个相似三角形中求解.常见模型如下:(点 为切点)
图4
图5
图6
图7
如图4, ;如图5, ;如图6,
;如图7, .
方法应用
图8
4.(2021·贺州)如图8,在 中, ,
,点 在 上, .以 为半径的 与
相切于点 ,交 于点 ,则 的长为( ) .
A. B. C. D.1
图46
提示:如图46,连接 , .
因为 与 相切于点 , 是 的直径,所以
, .因为 ,即 ,所
以 , .所以 ,
,则 , .因为 ,
【答案】B
,所以 , , .因此
, .解得 , .所以 .
微专题练习(十)
与切线性质有关的计算问题
类型一 切线与锐角三角函数的计算问题
图1
1.如图1, 为 的直径,点 在 的延长线上,
, 与 相切,切点分别为点 , .若
, ,则 等于( ) .
A. B. C. D.
图72
提示:如图72,连接 , , , 交 于点 .
因为 , 与 分别相切于点 , ,所以
, , 平分 .所以 ,
则 .所以 .因为 ,
【答案】D
所以 .在 中,
,所以 .因此
.
图2
2.如图2,已知 是 的直径, 与 相切于点 ,
连接 , .若 ,则 ___.
提示:因为 与 相切于点 ,所以 ,则 .在
中, ,因此设 ,则 由勾股
定理知, ,则
.所以 .
类型二 切线与勾股定理的计算问题
图3
3.(2023·重庆A卷)如图3, 是 的切线,
为切点,连接 , .若 ,
, ,则 的长是( ) .
A.3 B. C. D.6
图73
提示:如图73,连接 是 的切线,
.
, , , .
【答案】C
图4
4.(2022·宁波)如图4,在 中, ,
,点 在 上.以 为半径的圆与 相切于
点 , 是 边上的动点.当 为直角三角形
时, 的长为______.
图74
提示:如图74,连接 .
与 相切于点 , .由题意知,点
的位置分如下两种情况.①当 时,点
与点 重合,设 的半径 ,则 ,
.在 中,由勾股定理,得
,即 .解得 ,即
当 时, ,如图74,由
,得 . , ,
, .综上所述, 的长为 或 .
【答案】 或
类型三 坐标系中关于切线的计算问题
图5
5.(2021·河池)如图5,在平面直角坐标系中,以点
为圆心、 长为直径的圆与 轴相切,与 轴交
于 , 两点,则点 的坐标是___________.
图75
提示:如图75,
设以 为直径的圆与 轴相切于点 ,连接 , ,
交于点 ,则 轴, ,即 ,
则 轴.所以 .因为 ,所以
, ,则 .
在 中,由勾股定理,得
【答案】
.所以 .所
以 .
图6
6.如图6,在平面直角坐标系中,点 在第一象限,
与 轴、 轴都相切,且经过矩形 的顶点 ,与
相交于点 .若 的半径为5,点 的坐标是 ,
则点 的坐标是______.
图76
提示:如图76,设 与 轴、 轴的切点分别为点
, ,连接 , , ,延长 与 交于点 ,
则 轴, 轴, .又 ,
所以四边形 是正方形,则 ,
.由 知, ,则
.易知四边形 和四边形 是矩形,则
, , .在 中,因为 弦 ,
所以 , .所以 .
在 中,由勾股定理,得 .所
以 .所以 .
【答案】
类型四 切线与相似三角形的计算问题
图7
7.(2021·荆州)如图7, 是 的直径, 是 的
弦, 于点 ,连接 ,过点 作 交
于点 ,过点 的切线交 的延长线于点 .若 ,
,则 ___.
图7
提示: , , 为
的中点, 为 的中位线. .在
中,
是 的切线, ,即 .
【答案】
, .又 ,
,即 .解得 .
图8
8.(2020·梧州 改编)如图8,在矩形 中,
, ,点 在对角线 上,以 为
半径作 交 于点 ,连接 .若 是 的
切线,则此时 的半径为___.
小锦囊 由切线的性质知, , 是 的半径,因此求
出 即可.又 ,因此作 于点 ,可得
,就可根据相似三角形的对应边成比例列方程求解.
图77
提示:如图77,过点 作 于点 .
因为四边形 是矩形,所以 ,
, .在 中,
.因为
,所以设 ,
,则 .因为 , ,
所以 ,则 .因为 是 的切线,
所以 ,则 .又因为 ,
所以 .又因为 ,所以
,则 ,即 .解得 (舍去)或
.所以 .
【答案】
同课章节目录
