微专题 辅助圆最值问题 - 2024年中考数学复习课件(共49张PPT)
文档属性
| 名称 | 微专题 辅助圆最值问题 - 2024年中考数学复习课件(共49张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 22:01:22 | ||
图片预览








文档简介
(共49张PPT)
微专题 辅助圆最值问题
类型一 点圆最值
模型剖析 平面内一定点 和 上动点 的连线中,当连线过圆心
时,线段 有最大值和最小值.分以下情况讨论:(设 ,
的半径为 )
(1)点 在 外时, ,如图1、图2.
当 , , 三点在同一直线上时,线段 有最值: 的最大值为 , 的最小值为 .
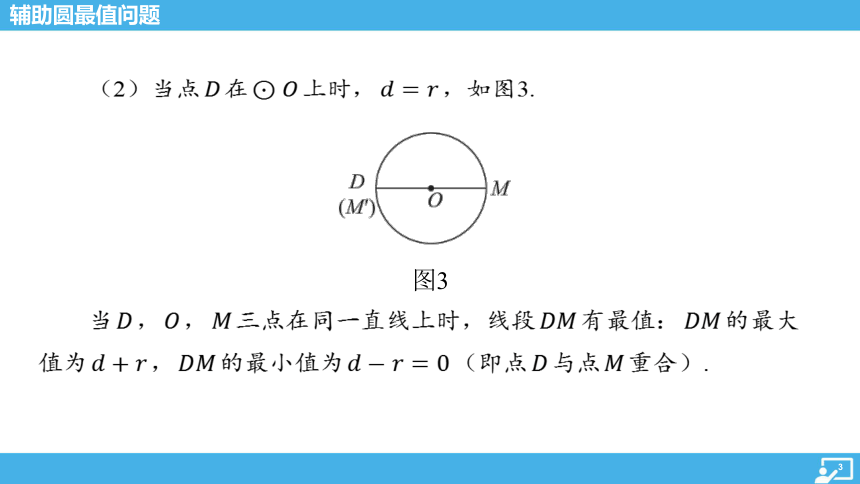
(2)当点 在 上时, ,如图3.
图3
当 , , 三点在同一直线上时,线段 有最值: 的最大
值为 , 的最小值为 (即点 与点 重合).
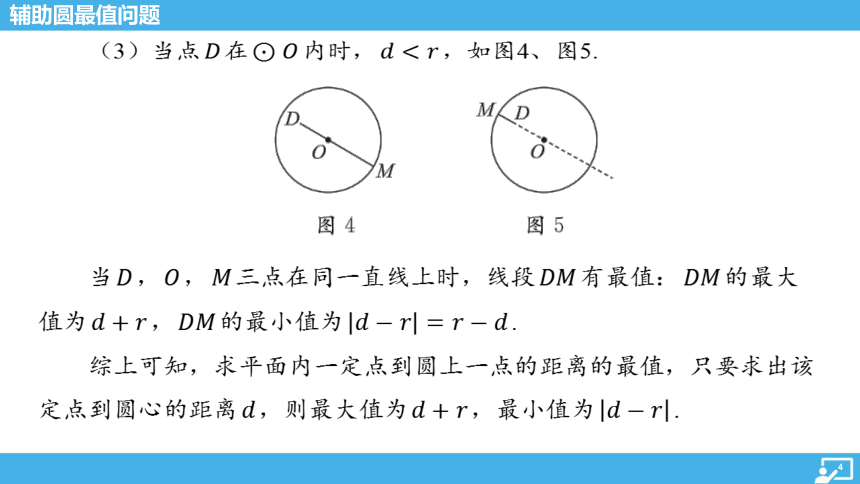
(3)当点 在 内时, ,如图4、图5.
当 , , 三点在同一直线上时,线段 有最值: 的最大
值为 , 的最小值为 .
综上可知,求平面内一定点到圆上一点的距离的最值,只要求出该
定点到圆心的距离 ,则最大值为 ,最小值为 .
模型应用
图6
1.(2023·台州)如图6, 的圆心 与正方形的中心重
合,已知 的半径和正方形的边长都为4,则圆上任意
一点到正方形边上任意一点距离的最小值为( ) .
D
A. B.2 C. D.
小锦囊 当圆的半径经过正方形的顶点时,圆上的点到正方形边上的点的距离取得最小值.
图7
2.如图7,在 中, ,
, ,点 是 的三等分点,半圆
与 相切, , 分别是 与半圆弧上的动
点,则 的最小值与最大值之和是( ) .
A.5 B.6 C.7 D.8
小锦囊 作 ,垂足为点 ,交半圆 于点 ,此时垂线段 最
短,当点 与点 重合,点 与点 重合时, 的值最小,且
;设半圆 与线段 的交点为 ,当点 与点 重合,点
与点 重合时, 经过圆心,此时 的值最大.
图47
提示:如图47,设半圆 与 相切于点 ,连接
.作 ,交 于点 ,垂足为点 ,此
时垂线段 的长最短, 的最小值 .在 中, , ,所以 .又因为点 是 的三等分点,
所以 .因为 , 所
以 ,则 .故 .所以 .因为
与 相切于点 ,所以 .因此 ,则 .
故 .所以 .故 .因此 的
最小值 .如图47,
当点 在 边上的点 处,点 与点 重合时, 经过圆心,经过圆心的弦最长.因此 的最大值 .所以 长的最大值与最小值的和是 .
图47
【答案】B
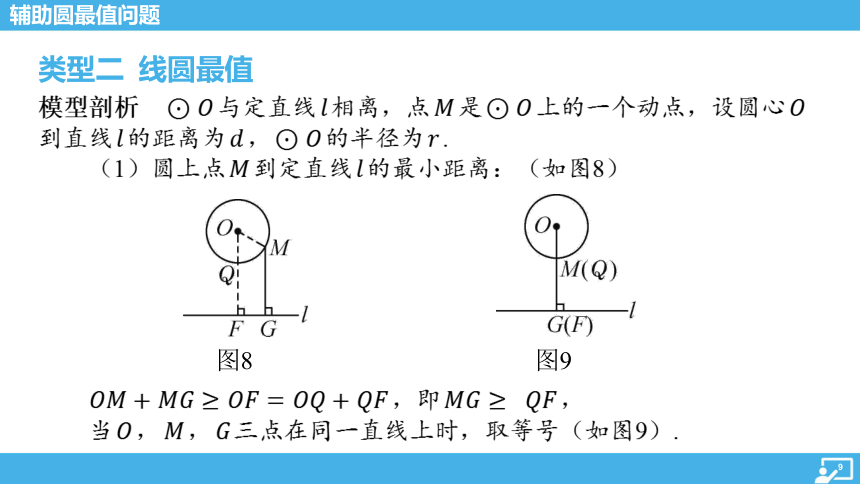
类型二 线圆最值
模型剖析 与定直线 相离,点 是 上的一个动点,设圆心
到直线 的距离为 , 的半径为 .
(1)圆上点 到定直线 的最小距离:(如图8)
图8
图9
,即 ,
当 , , 三点在同一直线上时,取等号(如图9).
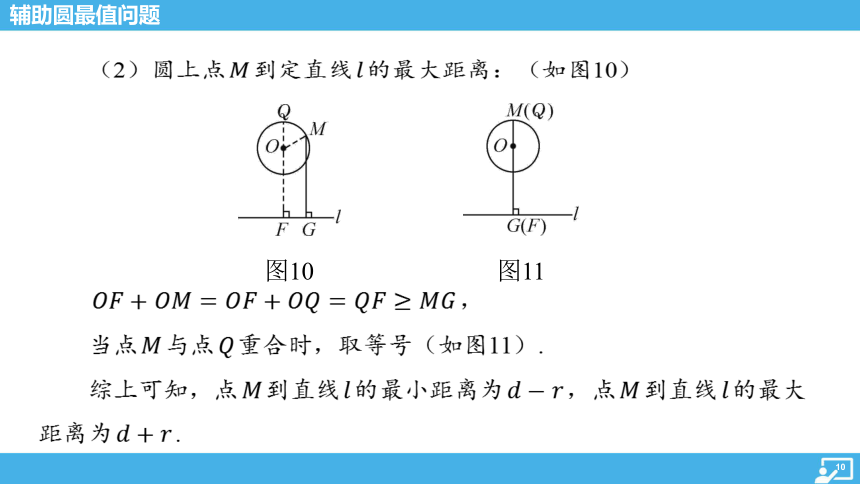
(2)圆上点 到定直线 的最大距离:(如图10)
图10
图11
,
当点 与点 重合时,取等号(如图11).
综上可知,点 到直线 的最小距离为 ,点 到直线 的最大
距离为 .
模型应用
3.(2023·宿迁)在同一平面内,已知 的半径为2,圆心 到直线 的
距离为3,点 为圆上的一个动点,则点 到直线 的最大距离是
( ) .
B
A.2 B.5 C.6 D.8
类型三 隐形圆最值
图12
(1)动点定长模型
模型剖析 如图12,若 为动点, ,则
, , 三点共圆,其中点 为圆心.
模型应用
4.已知等腰直角三角形 的腰长为4,点 在斜边 上,点 为该平
面内一动点,且满足 ,则 的最小值为( ) .
A.2 B. C. D.
图48
提示:如图48,因为等腰直角三角形 的腰长为4,所
以斜边长 .因为点 为该平面内一动点,且满足
,所以点 在以点 为圆心,2为半径的圆上.当点
在斜边 的高 上时, 的值最小.因为 是等
【答案】B
腰直角三角形,所以当 时, ,则 .
因为 ,所以 .
图13
(2)直角圆周角模型
模型剖析 如图13,若固定线段 所对动角 恒为 ,
则 , , 三点共圆,其中 为圆的直径.
模型应用
图14
5.如图14,在矩形 中, , , 是矩形内
部的一个动点,且 ,则 的最小值为_________.
图49
提示:如图49,因为 ,所以点 在以 的中
点 为圆心, 长为直径的一段弧(弧在矩形内部)
上运动.如图49,连接 交 于点 .当点 位于点
位置时,线段 的长取得最小值.在矩形 中,
,所以 .又 ,所以
.所以 .
图15
(3)定弦定角模型
模型剖析
如图15,固定线段 所对的动角 为定值,则 , ,
三点共圆.
模型应用
图16
6.如图16, 为等边三角形, .若 为 内
一动点,且满足 ,则线段 长的最小值为
_ ___.
图50
提示:因为 是等边三角形,所以 , .因为 ,所以 .所以 .因此点 运动形成的图形是以点 为圆心的 (如图50).当 , ,三点
在同一直线上时, 的长取得最小值.如图50,设 交 于点 ,此时 , ,则 , .所以 ,
.因此 .
【答案】
(4)四点共圆模型
模型剖析 如图17,若动角 动角 ,则 , , ,
四点共圆;如图18,若固定线段 所对同侧动角 ,则 ,
, , 四点共圆.
图17
图18
模型应用
图19
7.如图19,在 中, ,
, , 为 的中点.过点 作
, , 分别交射线 , 于点 , ,则
长的最小值为___.
图51
提示:如图51,连接 .因为 ,
, ,所以 .因为 为
的中点,所以 .因为 ,所以
.又 ,所以 , , , 四
【答案】2
点在以 为直径的圆上.因为 是圆的弦,所以 .所以当
,即 为直径时, 取得最小值.
类型四 阿氏圆最值
模型剖析 如图20,已知点 是 上一动点, , 为 外两定
点, 为 的半径.当 , 满足 时,求
的最小值(或 的最大值).
图20
求解时,如图21,可在 上截取线段 ,使 ,连接 , ,
可通过“两边对应成比例且夹角相等”得到 ,通过相似三角
形的对应边成比例,可将 转化为 ,从而 ,
连接 ,利用“两点之间线段最短”,将问题转化为求 的长.
图21
模型应用
图22
8.如图22,已知正方形 的边长为4, 的半径
为2,点 是 上的一个动点,则 的最小
值是___, 的最大值是___.
提示:如图52,在 上取一点 ,使 ,
, .又 ,
.
, 当 , , 三点在同一直线上时, 的值最小,最小值
,
当点 在 的延长线上时,
的值最大(如图53),
最大值 .
图52
图53
【答案】5; 5
微专题练习(十一)
辅助圆最值问题
类型一 点圆最值
图1
1.如图1, 的半径为1,圆心 的坐标为 ,
点 是 上的任意一点, ,且 ,
与 轴分别交于 , 两点.若点 , 关于原点
对称,则 的最小值为( ) .
C
A.3 B.4 C.6 D.8
图2
2.如图2,抛物线 与 轴交于 , 两
点, 是以点 为圆心,2为半径的圆上的动
点, 是线段 的中点,连接 ,则线段 长的
最大值是( ) .
A.3 B. C. D.4
图78
提示:如图78,连接 .当 时, ,
解得 , ,则 , 是
线段 的中点, 为 的中位线. .当 最大时, 最大.当 , , 三点在同一直线上,即 过圆心 时, 最大.如图78,点 运动
【答案】C
位置时, 最大. ,
线段 长的最大值是 .
类型二 线圆最值
图3
3.(2023·防城港二模)如图3,在平面直角坐标系
中,点 的坐标为 , 的半径为2, 为
轴上一动点, 切 于点 ,则 的最小值
是_____.
图4
4.(2023·陕西 节选)如图4,在 中,
, , .若
的半径为4,点 在 上,点 在 上,
连接 ,求线段 长的最小值.
图79
解:如图79,连接 , ,过点 作 ,垂足为点 ,则
的半径为4,
, , .
,
.
线段 长的最小值为 .
类型三 隐形圆最值
图5
5.如图5,点 , 的坐标分别为 , ,点
为坐标平面内一点, ,点 为线段 的中
点,连接 ,则 的最大值为( ) .
A. B. C. D.
图80
提示:如图80, 点 为坐标平面内一点,
, 点 在半径为1的 上.在 轴上取
,连接 , ,
是 的中位线. .当 最大
时, 最大.当 , , 三点共线,且点 在 的
延长线上时, 最大. , , . ,即 的最大值为 .
【答案】B
图6
6.(2020·贵港)如图6,动点 在边长为2的正方形
内运动,且 , 是 边上的一个动
点, 是 边的中点,则 的最小值为
( ) .
A. B. C. D.
图81
提示:如图81,作点 关于 的对称点 ,设 的中点为
点 ,连接 ,交 于点 ,连接 .因为动点 在边长
为2的正方形 内,且 ,所以点 在以 为
直径的圆上, .因为正方形 的边长为2,
所以 , .因为点 是 的中点,所以
.因为点 与点 关于 对称,所以
, .所以 .在
中, .所以线段
的最小值为 .
【答案】A
图7
7.如图7,在四边形 中, , , , 是 的中点,连接 ,则线段 长的最小值为_______.
图82
提示: , , , ,
四点共圆,且 为直径.如图82,取 的中点 ,
则圆心为点 ,连接 , ,取 的中点 ,连
接 , , .又
, 为等边三角形.
,
. 是 的中点, 是 的中
点, 是 的中位线. .在 中,
, 当 , , 三点在同一直线上时, 取得最小值,
最小值为 .
【答案】
8.(2021·清远)在 中, , , .点 为
平面上一个动点, ,则线段 长的最小值为_________.
图83
提示:如图83.∵ , , 作 的外接圆 (因求 最小值,故圆心 和点 在 的同侧),连接 , , ,当 , , 三点在同一直线上时, 的值最小. , . 为等腰直角三角形. ,
.又 , .
如图83,作 于点 , 为等腰直角三角形.
.在
中, .当 , , 三点在同一直线上时, 最小, .
【答案】
图83
类型四 阿氏圆最值
图8
9.如图8,在 中, , ,
, 的半径为2,点 是 上一动点,连接
, ,则 的最小值是_____.
图84
提示:如图84,在 上取点 ,使 ,连接
, , , . .又
, .
.要使
的值最小,只需 的值最小.当 , , 三点在
同一直线上时, 的值最小,最小值是 的长.此时
,
的最小值是 .
【答案】
图9
10.(2020·桂林)如图9,在 中,
,点 , 分别是 , 的中点,
点 是扇形 的 上任意一点,连接 ,
,则 的最小值是_____.
图85
提示:如图85,在 上取一点 ,使得 ,连接 , , , , , .又 , .
.在
中, , , ,
. . 的最小值为 .
【答案】
11.阅读以下材料,并按要求完成相应的任务.
已知平面上两点 , ,则所有符合
且 的点 会组成一个圆,
这个圆称为阿氏圆.
阿氏圆的基本解法:构造三角形相似.
【问题】 如图10,在平面直角坐标系中,在 轴、 轴上分别有点
, ,点 是平面内一动点,且 ,设 ,求
的最小值.
图10
阿氏圆的关键解题步骤:
第1步,如图10,在 上取点 ,使得 .
第2步,证明 .
第3步,连接 ,此时 的长即为所求的最小值.
下面是该题的解答过程(部分)
图10
解:在 上取点 ,使得 .
又 ,
.……
【任务】
(1)将以上解答过程补充完整.
解:在 上取点 ,使得 ,又 ,
.
当 , , 三点在同一直线上时, ,取得最小值.
在 中,由勾股定理,得 .
的最小值为 .
(2)如图11,在 中, , , , 为 内一动点,满足 ,求 的最小值.
图11
解:如图86,在 上取一点 ,使得 ,
连接 ,
, , , .
又 ,
.
.
图86
图86
当 , , 三点在同一直线上时, ,取得最小值, 的长即为 的最小值.
在 中, , , .
的最小值为 .
微专题 辅助圆最值问题
类型一 点圆最值
模型剖析 平面内一定点 和 上动点 的连线中,当连线过圆心
时,线段 有最大值和最小值.分以下情况讨论:(设 ,
的半径为 )
(1)点 在 外时, ,如图1、图2.
当 , , 三点在同一直线上时,线段 有最值: 的最大值为 , 的最小值为 .
(2)当点 在 上时, ,如图3.
图3
当 , , 三点在同一直线上时,线段 有最值: 的最大
值为 , 的最小值为 (即点 与点 重合).
(3)当点 在 内时, ,如图4、图5.
当 , , 三点在同一直线上时,线段 有最值: 的最大
值为 , 的最小值为 .
综上可知,求平面内一定点到圆上一点的距离的最值,只要求出该
定点到圆心的距离 ,则最大值为 ,最小值为 .
模型应用
图6
1.(2023·台州)如图6, 的圆心 与正方形的中心重
合,已知 的半径和正方形的边长都为4,则圆上任意
一点到正方形边上任意一点距离的最小值为( ) .
D
A. B.2 C. D.
小锦囊 当圆的半径经过正方形的顶点时,圆上的点到正方形边上的点的距离取得最小值.
图7
2.如图7,在 中, ,
, ,点 是 的三等分点,半圆
与 相切, , 分别是 与半圆弧上的动
点,则 的最小值与最大值之和是( ) .
A.5 B.6 C.7 D.8
小锦囊 作 ,垂足为点 ,交半圆 于点 ,此时垂线段 最
短,当点 与点 重合,点 与点 重合时, 的值最小,且
;设半圆 与线段 的交点为 ,当点 与点 重合,点
与点 重合时, 经过圆心,此时 的值最大.
图47
提示:如图47,设半圆 与 相切于点 ,连接
.作 ,交 于点 ,垂足为点 ,此
时垂线段 的长最短, 的最小值 .在 中, , ,所以 .又因为点 是 的三等分点,
所以 .因为 , 所
以 ,则 .故 .所以 .因为
与 相切于点 ,所以 .因此 ,则 .
故 .所以 .故 .因此 的
最小值 .如图47,
当点 在 边上的点 处,点 与点 重合时, 经过圆心,经过圆心的弦最长.因此 的最大值 .所以 长的最大值与最小值的和是 .
图47
【答案】B
类型二 线圆最值
模型剖析 与定直线 相离,点 是 上的一个动点,设圆心
到直线 的距离为 , 的半径为 .
(1)圆上点 到定直线 的最小距离:(如图8)
图8
图9
,即 ,
当 , , 三点在同一直线上时,取等号(如图9).
(2)圆上点 到定直线 的最大距离:(如图10)
图10
图11
,
当点 与点 重合时,取等号(如图11).
综上可知,点 到直线 的最小距离为 ,点 到直线 的最大
距离为 .
模型应用
3.(2023·宿迁)在同一平面内,已知 的半径为2,圆心 到直线 的
距离为3,点 为圆上的一个动点,则点 到直线 的最大距离是
( ) .
B
A.2 B.5 C.6 D.8
类型三 隐形圆最值
图12
(1)动点定长模型
模型剖析 如图12,若 为动点, ,则
, , 三点共圆,其中点 为圆心.
模型应用
4.已知等腰直角三角形 的腰长为4,点 在斜边 上,点 为该平
面内一动点,且满足 ,则 的最小值为( ) .
A.2 B. C. D.
图48
提示:如图48,因为等腰直角三角形 的腰长为4,所
以斜边长 .因为点 为该平面内一动点,且满足
,所以点 在以点 为圆心,2为半径的圆上.当点
在斜边 的高 上时, 的值最小.因为 是等
【答案】B
腰直角三角形,所以当 时, ,则 .
因为 ,所以 .
图13
(2)直角圆周角模型
模型剖析 如图13,若固定线段 所对动角 恒为 ,
则 , , 三点共圆,其中 为圆的直径.
模型应用
图14
5.如图14,在矩形 中, , , 是矩形内
部的一个动点,且 ,则 的最小值为_________.
图49
提示:如图49,因为 ,所以点 在以 的中
点 为圆心, 长为直径的一段弧(弧在矩形内部)
上运动.如图49,连接 交 于点 .当点 位于点
位置时,线段 的长取得最小值.在矩形 中,
,所以 .又 ,所以
.所以 .
图15
(3)定弦定角模型
模型剖析
如图15,固定线段 所对的动角 为定值,则 , ,
三点共圆.
模型应用
图16
6.如图16, 为等边三角形, .若 为 内
一动点,且满足 ,则线段 长的最小值为
_ ___.
图50
提示:因为 是等边三角形,所以 , .因为 ,所以 .所以 .因此点 运动形成的图形是以点 为圆心的 (如图50).当 , ,三点
在同一直线上时, 的长取得最小值.如图50,设 交 于点 ,此时 , ,则 , .所以 ,
.因此 .
【答案】
(4)四点共圆模型
模型剖析 如图17,若动角 动角 ,则 , , ,
四点共圆;如图18,若固定线段 所对同侧动角 ,则 ,
, , 四点共圆.
图17
图18
模型应用
图19
7.如图19,在 中, ,
, , 为 的中点.过点 作
, , 分别交射线 , 于点 , ,则
长的最小值为___.
图51
提示:如图51,连接 .因为 ,
, ,所以 .因为 为
的中点,所以 .因为 ,所以
.又 ,所以 , , , 四
【答案】2
点在以 为直径的圆上.因为 是圆的弦,所以 .所以当
,即 为直径时, 取得最小值.
类型四 阿氏圆最值
模型剖析 如图20,已知点 是 上一动点, , 为 外两定
点, 为 的半径.当 , 满足 时,求
的最小值(或 的最大值).
图20
求解时,如图21,可在 上截取线段 ,使 ,连接 , ,
可通过“两边对应成比例且夹角相等”得到 ,通过相似三角
形的对应边成比例,可将 转化为 ,从而 ,
连接 ,利用“两点之间线段最短”,将问题转化为求 的长.
图21
模型应用
图22
8.如图22,已知正方形 的边长为4, 的半径
为2,点 是 上的一个动点,则 的最小
值是___, 的最大值是___.
提示:如图52,在 上取一点 ,使 ,
, .又 ,
.
, 当 , , 三点在同一直线上时, 的值最小,最小值
,
当点 在 的延长线上时,
的值最大(如图53),
最大值 .
图52
图53
【答案】5; 5
微专题练习(十一)
辅助圆最值问题
类型一 点圆最值
图1
1.如图1, 的半径为1,圆心 的坐标为 ,
点 是 上的任意一点, ,且 ,
与 轴分别交于 , 两点.若点 , 关于原点
对称,则 的最小值为( ) .
C
A.3 B.4 C.6 D.8
图2
2.如图2,抛物线 与 轴交于 , 两
点, 是以点 为圆心,2为半径的圆上的动
点, 是线段 的中点,连接 ,则线段 长的
最大值是( ) .
A.3 B. C. D.4
图78
提示:如图78,连接 .当 时, ,
解得 , ,则 , 是
线段 的中点, 为 的中位线. .当 最大时, 最大.当 , , 三点在同一直线上,即 过圆心 时, 最大.如图78,点 运动
【答案】C
位置时, 最大. ,
线段 长的最大值是 .
类型二 线圆最值
图3
3.(2023·防城港二模)如图3,在平面直角坐标系
中,点 的坐标为 , 的半径为2, 为
轴上一动点, 切 于点 ,则 的最小值
是_____.
图4
4.(2023·陕西 节选)如图4,在 中,
, , .若
的半径为4,点 在 上,点 在 上,
连接 ,求线段 长的最小值.
图79
解:如图79,连接 , ,过点 作 ,垂足为点 ,则
的半径为4,
, , .
,
.
线段 长的最小值为 .
类型三 隐形圆最值
图5
5.如图5,点 , 的坐标分别为 , ,点
为坐标平面内一点, ,点 为线段 的中
点,连接 ,则 的最大值为( ) .
A. B. C. D.
图80
提示:如图80, 点 为坐标平面内一点,
, 点 在半径为1的 上.在 轴上取
,连接 , ,
是 的中位线. .当 最大
时, 最大.当 , , 三点共线,且点 在 的
延长线上时, 最大. , , . ,即 的最大值为 .
【答案】B
图6
6.(2020·贵港)如图6,动点 在边长为2的正方形
内运动,且 , 是 边上的一个动
点, 是 边的中点,则 的最小值为
( ) .
A. B. C. D.
图81
提示:如图81,作点 关于 的对称点 ,设 的中点为
点 ,连接 ,交 于点 ,连接 .因为动点 在边长
为2的正方形 内,且 ,所以点 在以 为
直径的圆上, .因为正方形 的边长为2,
所以 , .因为点 是 的中点,所以
.因为点 与点 关于 对称,所以
, .所以 .在
中, .所以线段
的最小值为 .
【答案】A
图7
7.如图7,在四边形 中, , , , 是 的中点,连接 ,则线段 长的最小值为_______.
图82
提示: , , , ,
四点共圆,且 为直径.如图82,取 的中点 ,
则圆心为点 ,连接 , ,取 的中点 ,连
接 , , .又
, 为等边三角形.
,
. 是 的中点, 是 的中
点, 是 的中位线. .在 中,
, 当 , , 三点在同一直线上时, 取得最小值,
最小值为 .
【答案】
8.(2021·清远)在 中, , , .点 为
平面上一个动点, ,则线段 长的最小值为_________.
图83
提示:如图83.∵ , , 作 的外接圆 (因求 最小值,故圆心 和点 在 的同侧),连接 , , ,当 , , 三点在同一直线上时, 的值最小. , . 为等腰直角三角形. ,
.又 , .
如图83,作 于点 , 为等腰直角三角形.
.在
中, .当 , , 三点在同一直线上时, 最小, .
【答案】
图83
类型四 阿氏圆最值
图8
9.如图8,在 中, , ,
, 的半径为2,点 是 上一动点,连接
, ,则 的最小值是_____.
图84
提示:如图84,在 上取点 ,使 ,连接
, , , . .又
, .
.要使
的值最小,只需 的值最小.当 , , 三点在
同一直线上时, 的值最小,最小值是 的长.此时
,
的最小值是 .
【答案】
图9
10.(2020·桂林)如图9,在 中,
,点 , 分别是 , 的中点,
点 是扇形 的 上任意一点,连接 ,
,则 的最小值是_____.
图85
提示:如图85,在 上取一点 ,使得 ,连接 , , , , , .又 , .
.在
中, , , ,
. . 的最小值为 .
【答案】
11.阅读以下材料,并按要求完成相应的任务.
已知平面上两点 , ,则所有符合
且 的点 会组成一个圆,
这个圆称为阿氏圆.
阿氏圆的基本解法:构造三角形相似.
【问题】 如图10,在平面直角坐标系中,在 轴、 轴上分别有点
, ,点 是平面内一动点,且 ,设 ,求
的最小值.
图10
阿氏圆的关键解题步骤:
第1步,如图10,在 上取点 ,使得 .
第2步,证明 .
第3步,连接 ,此时 的长即为所求的最小值.
下面是该题的解答过程(部分)
图10
解:在 上取点 ,使得 .
又 ,
.……
【任务】
(1)将以上解答过程补充完整.
解:在 上取点 ,使得 ,又 ,
.
当 , , 三点在同一直线上时, ,取得最小值.
在 中,由勾股定理,得 .
的最小值为 .
(2)如图11,在 中, , , , 为 内一动点,满足 ,求 的最小值.
图11
解:如图86,在 上取一点 ,使得 ,
连接 ,
, , , .
又 ,
.
.
图86
图86
当 , , 三点在同一直线上时, ,取得最小值, 的长即为 的最小值.
在 中, , , .
的最小值为 .
同课章节目录
