人教版六年级数学下册第三单元《圆柱与圆锥》单元培优卷(含答案)
文档属性
| 名称 | 人教版六年级数学下册第三单元《圆柱与圆锥》单元培优卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 347.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 20:43:41 | ||
图片预览


文档简介
六年级数学下册第三单元《圆柱与圆锥》单元培优卷
一、选择题(共8小题,每小题2分,满分16分)
1.下面的图以直线为轴快速旋转后形成的图形是( )。
A. B. C. D.
2.一个圆柱的侧面展开图是一个正方形,这个圆柱的底面直径与高的比是( )。
A.: B.: C.: D.:
3.一张长方形纸可以沿长边或短边围成不同的圆柱形纸筒(如图)。如果给两个纸筒都配上两个底面,则圆柱①的表面积与圆柱②的表面积相比,( )。
A.圆柱①的表面积大 B.圆柱②的表面积大
C.两个圆柱的表面积相等 D.无法比较
4.一张长方形纸片,以虚线为轴旋转一周,( )形成的圆柱体积最大。
A. B.
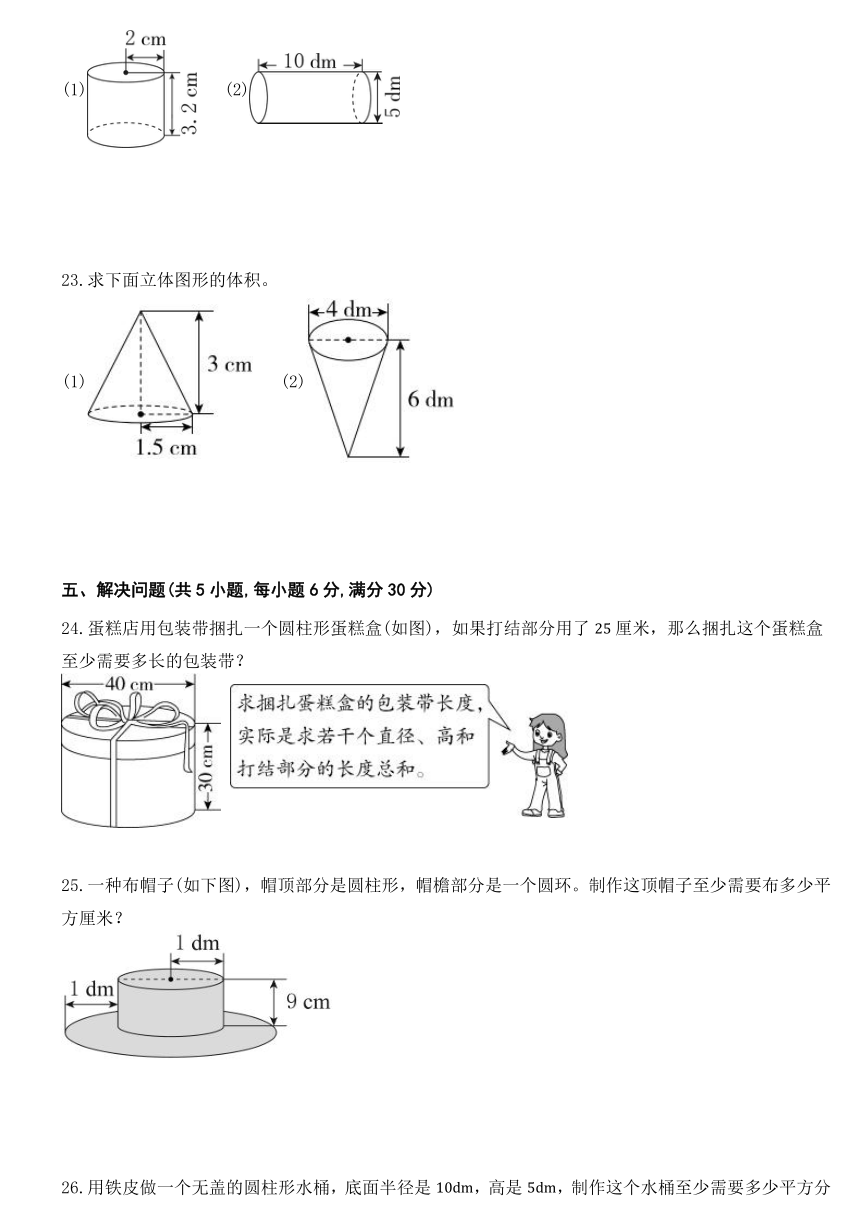
C. D.
5.以下能准确测量出圆锥高的方法是( )。
A. B. C. D.
6.把一个高是厘米的圆柱沿底面直径切开,切面是一个长方形,这个长方形的长是厘米,宽是厘米,那么原来这个圆柱的体积是( )立方厘米。
A. B. C. D.
7.若圆柱和圆锥的体积相等,底面积也相等,且圆锥的高是,则圆柱高为( )。
A. B. C.
8.如下图,圆柱形容器里的沙子占容器容积的,倒入空的圆锥形容器( )内正好倒满。(单位:)
A. B. C. D.
二、判断题(共5小题,每小题2分,满分10分)
9.上、下两个底面相等的物体一定是圆柱。( )
10.两个圆柱的侧面积相等,它们的体积也一定相等。( )
11.求圆柱形容器的容积,就是求这个容器里面能容纳的物体的体积。( )
12.同圆柱一样,圆锥也有无数条高。( )
13.若两个圆柱的侧面积相等,则它们的底面周长也一定相等。( )
三、填空题(共8小题,每小题3分,满分24分)
14.一个圆柱形学具,底面直径是厘米,高是厘米。如果做一个有盖的长方体纸盒,使圆柱形学具正好能装进去,至少需要( )平方厘米的硬纸板。(得数保留整十数)
15.一个圆柱的底面半径是, 高是, 这个圆柱的底面积是( ), 侧面积是( ), 表面积是( )。
16.一个圆锥形麦堆,底面周长是,高是,这堆小麦的体积是( )。
17.一个圆柱的侧面展开图是一个正方形,这个圆柱的高是,那么它的底面周长是( ), 底面直径是( )。
18.把一根米长的圆柱形钢锭截成两个小圆柱,表面积增加了平方分米,这根圆柱形钢锭的体积是( )立方分米。
19.一个圆柱的底面半径扩大到原来的倍,高不变,体积扩大到原来的( )倍。
20.一个圆柱的体积为,与它等底等高的圆锥的体积为( )。
21.一个盛满水的圆锥形容器,量得水深,将水全部倒入和它等底等高的圆柱形容器里,水深是( )。
四、计算题(共2小题,每小题10分,满分20分)
22.计算下列图形的表面积。
(1) (2)
23.求下面立体图形的体积。
(1) (2)
五、解决问题(共5小题,每小题6分,满分30分)
24.蛋糕店用包装带捆扎一个圆柱形蛋糕盒(如图),如果打结部分用了厘米,那么捆扎这个蛋糕盒至少需要多长的包装带?
25.一种布帽子(如下图),帽顶部分是圆柱形,帽檐部分是一个圆环。制作这顶帽子至少需要布多少平方厘米?
26.用铁皮做一个无盖的圆柱形水桶,底面半径是,高是,制作这个水桶至少需要多少平方分米的铁皮?这个水桶的容积是多少?(铁皮厚度忽略不计)
27.一个圆锥形的沙堆,它的占地面积是,高是,每立方米沙子重。用一辆载质量为的汽车把这堆沙子运走,至少要几次才能运完?
28.一个药瓶,它的瓶身呈圆柱形(不包括瓶颈),如下图所示,瓶内药水的体积为。瓶子正放时,瓶内液面的高为,瓶子倒放时,空余部分高。这个瓶子的容积是多少立方厘米?
参考答案
1.C
2.B
3.B
4.B
5.D
6.A
7.A
【解析】根据等底等高的圆柱体积是圆锥体积的倍,若圆柱和圆锥的体积相等,底面积也相等,则圆柱的高是圆锥高的。
8.A
9.错
10.错
【解析】圆柱侧面积底面周长高,圆柱体积底面积高,因为它们的侧面面积相等,但底面半径和高不一定相等,所以体积也不一定相等。
11.对
12.错
13.错
14.
15.;;
16.
17.;
18.
【解析】钢锭截成两个小圆柱后表面积增加了平方分米,即钢锭的底面积是(平方分米),米分米,则钢锭的体积为(立方分米)。
19.
20.
21.
【解析】因为等底等高的圆锥的体积是圆柱体积的,所以当圆锥和圆柱的体积相等,底面积相等时,圆柱的高是圆锥高的,即(厘米),故圆柱形容器中水深厘米。
22.(1)
(2)
23.(1)(立方厘米)
(2)(分米)(立方分米)
24.(厘米)
【解析】包装带的长度等于个直径、条高和打结部分的长度和。
25.分米厘米
(平方厘米)
(平方厘米)
(平方厘米)
(平方厘米)
答:制作这顶帽子至少需要布平方厘米。
26.
答:制作这个水桶至少需要的铁皮,这个水桶的容积是。
【解析】求制作这个水桶至少需要多少平方分米铁皮,就是求圆柱的侧面积底面积,圆柱的侧面积 底面周长高,底面积;求这个水桶的容积是多少利用圆柱的体积公式计算。
27.(次)
答:至少要次才能运完。
28.
答:这个瓶子的容积是。
【解析】解答此题的关键是理解:瓶子的总体积不变,瓶中药水的体积不变,所以瓶中空气的体积也不会变,可以将左图中不规则的空气体积转化为右图中规则的空气体积。
所以:瓶子的体积左瓶中圆柱形药水的体积右瓶中圆柱形空气的体积。
根据题目中的已知条件,左瓶中圆柱形药水的体积已知为立方厘米,再用求出瓶子的底面积,即可计算出右瓶中圆柱形空气的体积,进而求出瓶子的体积。
一、选择题(共8小题,每小题2分,满分16分)
1.下面的图以直线为轴快速旋转后形成的图形是( )。
A. B. C. D.
2.一个圆柱的侧面展开图是一个正方形,这个圆柱的底面直径与高的比是( )。
A.: B.: C.: D.:
3.一张长方形纸可以沿长边或短边围成不同的圆柱形纸筒(如图)。如果给两个纸筒都配上两个底面,则圆柱①的表面积与圆柱②的表面积相比,( )。
A.圆柱①的表面积大 B.圆柱②的表面积大
C.两个圆柱的表面积相等 D.无法比较
4.一张长方形纸片,以虚线为轴旋转一周,( )形成的圆柱体积最大。
A. B.
C. D.
5.以下能准确测量出圆锥高的方法是( )。
A. B. C. D.
6.把一个高是厘米的圆柱沿底面直径切开,切面是一个长方形,这个长方形的长是厘米,宽是厘米,那么原来这个圆柱的体积是( )立方厘米。
A. B. C. D.
7.若圆柱和圆锥的体积相等,底面积也相等,且圆锥的高是,则圆柱高为( )。
A. B. C.
8.如下图,圆柱形容器里的沙子占容器容积的,倒入空的圆锥形容器( )内正好倒满。(单位:)
A. B. C. D.
二、判断题(共5小题,每小题2分,满分10分)
9.上、下两个底面相等的物体一定是圆柱。( )
10.两个圆柱的侧面积相等,它们的体积也一定相等。( )
11.求圆柱形容器的容积,就是求这个容器里面能容纳的物体的体积。( )
12.同圆柱一样,圆锥也有无数条高。( )
13.若两个圆柱的侧面积相等,则它们的底面周长也一定相等。( )
三、填空题(共8小题,每小题3分,满分24分)
14.一个圆柱形学具,底面直径是厘米,高是厘米。如果做一个有盖的长方体纸盒,使圆柱形学具正好能装进去,至少需要( )平方厘米的硬纸板。(得数保留整十数)
15.一个圆柱的底面半径是, 高是, 这个圆柱的底面积是( ), 侧面积是( ), 表面积是( )。
16.一个圆锥形麦堆,底面周长是,高是,这堆小麦的体积是( )。
17.一个圆柱的侧面展开图是一个正方形,这个圆柱的高是,那么它的底面周长是( ), 底面直径是( )。
18.把一根米长的圆柱形钢锭截成两个小圆柱,表面积增加了平方分米,这根圆柱形钢锭的体积是( )立方分米。
19.一个圆柱的底面半径扩大到原来的倍,高不变,体积扩大到原来的( )倍。
20.一个圆柱的体积为,与它等底等高的圆锥的体积为( )。
21.一个盛满水的圆锥形容器,量得水深,将水全部倒入和它等底等高的圆柱形容器里,水深是( )。
四、计算题(共2小题,每小题10分,满分20分)
22.计算下列图形的表面积。
(1) (2)
23.求下面立体图形的体积。
(1) (2)
五、解决问题(共5小题,每小题6分,满分30分)
24.蛋糕店用包装带捆扎一个圆柱形蛋糕盒(如图),如果打结部分用了厘米,那么捆扎这个蛋糕盒至少需要多长的包装带?
25.一种布帽子(如下图),帽顶部分是圆柱形,帽檐部分是一个圆环。制作这顶帽子至少需要布多少平方厘米?
26.用铁皮做一个无盖的圆柱形水桶,底面半径是,高是,制作这个水桶至少需要多少平方分米的铁皮?这个水桶的容积是多少?(铁皮厚度忽略不计)
27.一个圆锥形的沙堆,它的占地面积是,高是,每立方米沙子重。用一辆载质量为的汽车把这堆沙子运走,至少要几次才能运完?
28.一个药瓶,它的瓶身呈圆柱形(不包括瓶颈),如下图所示,瓶内药水的体积为。瓶子正放时,瓶内液面的高为,瓶子倒放时,空余部分高。这个瓶子的容积是多少立方厘米?
参考答案
1.C
2.B
3.B
4.B
5.D
6.A
7.A
【解析】根据等底等高的圆柱体积是圆锥体积的倍,若圆柱和圆锥的体积相等,底面积也相等,则圆柱的高是圆锥高的。
8.A
9.错
10.错
【解析】圆柱侧面积底面周长高,圆柱体积底面积高,因为它们的侧面面积相等,但底面半径和高不一定相等,所以体积也不一定相等。
11.对
12.错
13.错
14.
15.;;
16.
17.;
18.
【解析】钢锭截成两个小圆柱后表面积增加了平方分米,即钢锭的底面积是(平方分米),米分米,则钢锭的体积为(立方分米)。
19.
20.
21.
【解析】因为等底等高的圆锥的体积是圆柱体积的,所以当圆锥和圆柱的体积相等,底面积相等时,圆柱的高是圆锥高的,即(厘米),故圆柱形容器中水深厘米。
22.(1)
(2)
23.(1)(立方厘米)
(2)(分米)(立方分米)
24.(厘米)
【解析】包装带的长度等于个直径、条高和打结部分的长度和。
25.分米厘米
(平方厘米)
(平方厘米)
(平方厘米)
(平方厘米)
答:制作这顶帽子至少需要布平方厘米。
26.
答:制作这个水桶至少需要的铁皮,这个水桶的容积是。
【解析】求制作这个水桶至少需要多少平方分米铁皮,就是求圆柱的侧面积底面积,圆柱的侧面积 底面周长高,底面积;求这个水桶的容积是多少利用圆柱的体积公式计算。
27.(次)
答:至少要次才能运完。
28.
答:这个瓶子的容积是。
【解析】解答此题的关键是理解:瓶子的总体积不变,瓶中药水的体积不变,所以瓶中空气的体积也不会变,可以将左图中不规则的空气体积转化为右图中规则的空气体积。
所以:瓶子的体积左瓶中圆柱形药水的体积右瓶中圆柱形空气的体积。
根据题目中的已知条件,左瓶中圆柱形药水的体积已知为立方厘米,再用求出瓶子的底面积,即可计算出右瓶中圆柱形空气的体积,进而求出瓶子的体积。
