2024年中考数学模拟试卷二(含答案)

2024年中考数学模拟试卷 (二)
说 明: 1. 全卷满分 150分,考试时间 120 分钟。
2. 本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共三个大题26个小题。
第Ⅰ卷 选择题(共 30 分)
一、选择题(下列每小题给出的四个选项中，只有一个是符合题意的.每小题3分，共30分)
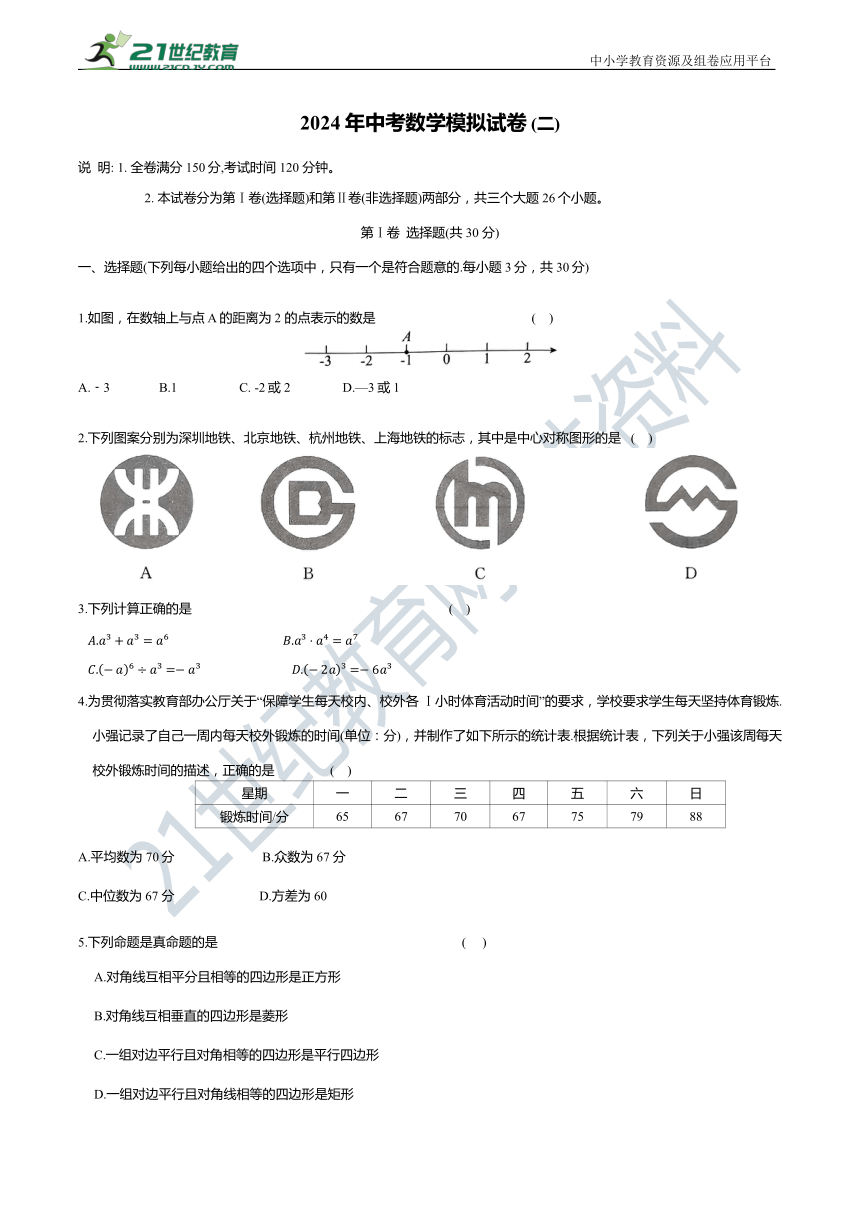
1.如图，在数轴上与点 A 的距离为 2 的点表示的数是 ( )
A.﹣3 B.1 C. -2或2 D.—3或1
2.下列图案分别为深圳地铁、北京地铁、杭州地铁、上海地铁的标志，其中是中心对称图形的是 ( )
3.下列计算正确的是 ( )
4.为贯彻落实教育部办公厅关于“保障学生每天校内、校外各 Ⅰ小时体育活动时间”的要求，学校要求学生每天坚持体育锻炼.小强记录了自己一周内每天校外锻炼的时间(单位：分)，并制作了如下所示的统计表.根据统计表，下列关于小强该周每天校外锻炼时间的描述，正确的是 ( )
星期 一 二 三 四 五 六 日
锻炼时间/分 65 67 70 67 75 79 88
A.平均数为70分 B.众数为 67 分
C.中位数为 67 分 D.方差为 60
5.下列命题是真命题的是 ( )
A.对角线互相平分且相等的四边形是正方形
B.对角线互相垂直的四边形是菱形
C.一组对边平行且对角相等的四边形是平行四边形
D.一组对边平行且对角线相等的四边形是矩形
6.元代数学家朱世杰于 1303 年编著的《四元玉鉴》中有这样一道题目：“九百九十九文钱，及时梨果买一千，一十一文梨九个，七枚果子四文钱.问：梨果多少价几何 ”此题的题意是：用999 文钱买得梨和果共1000个，梨11 文买9个，果4 文买7 个.问买梨、果各几个，各付多少钱 设付梨钱 x文，根据题意可列出的方程是 （ ）
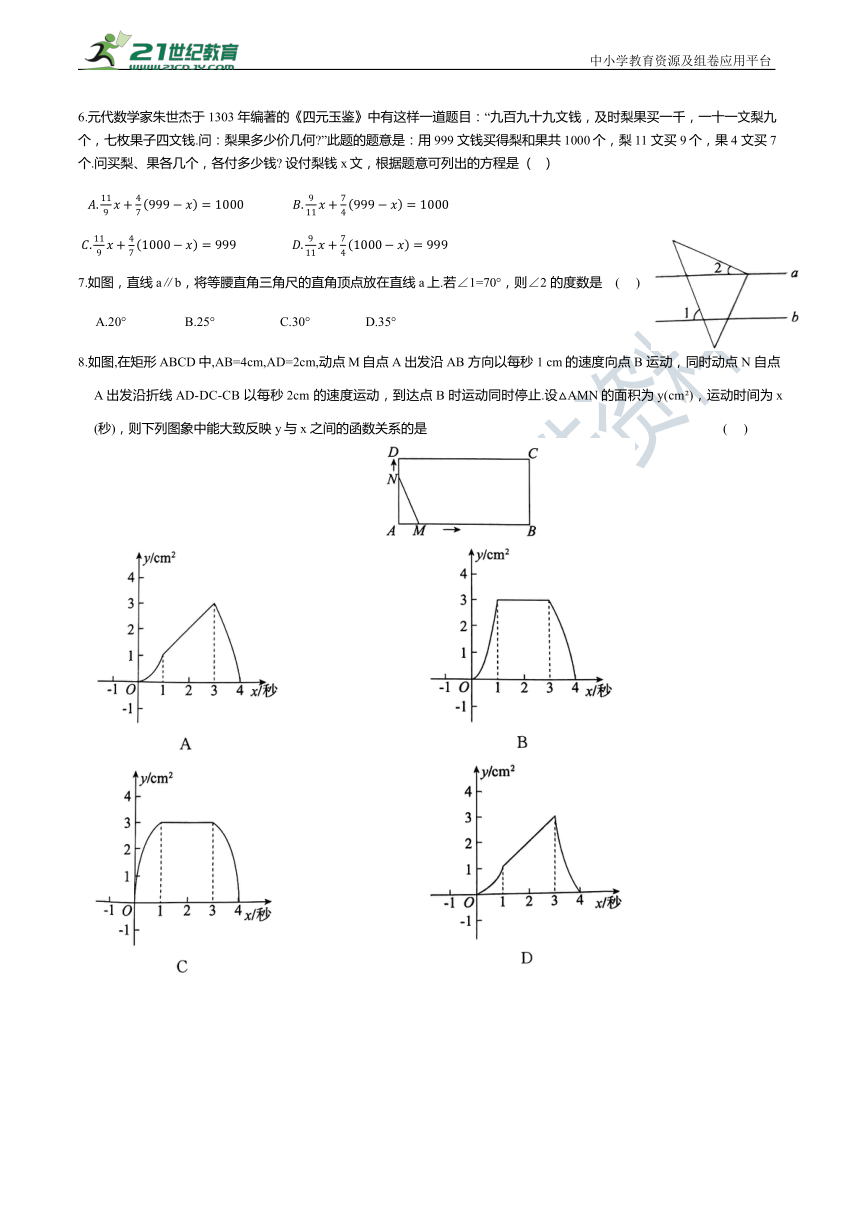
7.如图，直线 a∥b，将等腰直角三角尺的直角顶点放在直线a上.若∠1=70°，则∠2 的度数是 ( )
A.20° B.25° C.30° D.35°
8.如图,在矩形 ABCD中,AB=4cm,AD=2cm,动点M自点A 出发沿AB 方向以每秒1 cm的速度向点 B 运动，同时动点 N 自点 A 出发沿折线AD-DC-CB 以每秒2cm 的速度运动，到达点 B 时运动同时停止.设△AMN的面积为y(cm )，运动时间为x(秒)，则下列图象中能大致反映 y与x 之间的函数关系的是 ( )
中小学教育资源及组卷应用平台
9.如图,在 ABCD中,∠A=45°.利用尺规在 BC,BA 上分别截取BE,BF,使 ;分别以点 E,F为圆心，大于 EF 的长为半径作弧,两弧在∠CBA 的内部交于点O;作射线 BO 交 DC 于点 H,则 tan∠CHB的值为 ( )
B.
D.2
10.如图，已知开口向上的抛物线 与x 轴交于点(-1，0)，对称轴为直线 x=1，则下列结论正确的有 ( )
①2a+b=0;
②函数 的最小值为-4a；
③若关于 x 的方程 无实数根，则
④代数式((a-b)(b-c)(c-a)<0.
A.1个 B.2个 C.3个 D.4个
第Ⅱ卷 非选择题(共120 分)
二、填空题(每小题4分，共 24分)
11.据广元统计局发布的《广元统计数据——2023》显示，广元 2022年汽车保有量约为352 000 辆.将数据 352000用科学记数法表示为 .
12.某校计划组织八年级学生进行研学活动，现有四个地点可供选择：剑门关、皇泽寺、唐家河自然保护区、昭化古镇.若从中随机选择一个地点，则选中“剑门关”的概率为 .
13.若两个不相等的实数m，n分别满足 则 的值是 .
14.如图,在扇形 AOB中,∠AOB=90°,将扇形 AOB 进行折叠,使点 O 落在弧AB 的中点C 处.若折痕 则图中阴影部分的面积为 .
15.如图，将大小不同的两块直角三角尺 ABC和ADE 摆放在平面直角坐标系xOy 中，三角尺 ADE的直角边AD在x 轴上,∠ °，反比例函数 的图象恰好经过点 B，E.若 则
16.如图,在四边形 ABCD 中, ,则 AD 的长为 .
三、解答题(要求写出必要的解答步骤或证明过程，共 96 分)
17.(6分)解方程：
18.(8分)先化简，再求值： 其中 x 满足
19.(9分)如图，在 中, ,D 是 边 AB 上一点, ,过点 D 作 于E ,过点 C 作( 于F .
(1)求证:
(2)若 求 的面积.
20.(9分)某学校图书馆典范项目为学校配置了甲、乙两种经典读本各若干本，项目第一批购进甲、乙两种读本分别花费了 12000元和9000 元，甲种经典读本的单价是乙种经典读本单价的 1.2倍，并且甲种经典读本的数量比乙种经典读本的数量多100本.
(1)求购进这两种经典读本分别是多少本；
(2)若图书馆项目第二批购进这两种经典读本共1300本，其中购进甲种经典读本的数量不低于600本，且购进两种读本的总费用不超过14 500元，求购进这两种经典读本的最低总费用.
21.(9分)6月5日是世界环境日，为提高学生的环保意识，培养学生的劳动习惯，张老师随机对本班部分学生周末打扫卫生情况进行了为期半个月的跟踪调查，将调查结果分成四类，A：特别好；B：好；C：一般；D：较差.并将调查结果绘制成如下两幅不完整的统计图，请你根据统计图解答下列问题：
(1)本次调查中，张老师一共调查了 名同学，并将上面的条形统计图补充完整；
(2)若该班所在的年级共有 400名学生，请估计该年级 A 类学生的人数；
(3)张老师想从被调查的 A 类学生中选取一位同学对D类学生中一位同学进行结对互助学习，请用列表法或画树状图法求出结对互助学习都是男同学的概率.
22.(9分)小华同学乘坐摩天轮时发现，当小华在摩天轮客舱中上升到点 B位置时，测得C 处的俯角是( 测得 A处的俯角是 ，如图所示.已知摩天轮最低点 A 距离地面的高度. )米，求小华在 B处时距离地面的高度.(结果保留根号)
23.(10分)如图，在平面直角坐标系xOy中，一次函数 的图象与反比例函数 的图象在第一象限相交于A(1,4),B(m,1)两点.
(1)求一次函数和反比例函数的解析式；
(2)过点 A 作. ，交该反比例函数图象于另一点 C，连接 BC，求 BC的长.
24.(10 分)如图，AB为⊙O的直径，D为AB 延长线上一点，BC是⊙O的弦，过点O作( )于点E,交CD于点F,
(1)求证:CD为⊙O的切线;
(2)若 求⊙O的半径.
25.(12 分)【问题呈现】
(1)如图1，将直角尺的直角顶点摆放在正方形ABCD 的对角线交点O 处，直角尺两直角边分别交正方形的边 AB,BC于点M,N,求证:OM=ON.
【问题探究】
(2)若将(1)中的正方形 ABCD 更换为矩形ABCD,且 BC=kAB,如图2,判断OM 与ON 的等量关系(用含 k的式子表示)，并说明理由.
【问题再探究】
(3)将图2中的∠MON 的顶点O 沿OC 方向平移至点 P,若 PA=aPC,如图 3,请直接写出 PM与PN 的等量关系(用含 k，a的式子表示，不需证明).
【拓展运用】
(4)如图4,若AB=2BC,点 N在边 BC上,∠BPN=∠BAC,延长 NP交边 CD 于点 G,若 b,求b的值.
26.(14分)如图，二次函数 的图象与x 轴交于原点O 和点 A(4，0)，经过点 A 的直线与该函数图象交于另一点B(1，3)，与y轴交于点C.
(1)求直线 AB 的函数解析式及点C 的坐标.
(2)点 P 是抛物线上位于直线AB 上方的一个动点，过点 P 作直线. 轴于点E，与直线 AB 交于点 D,过点 B 作. 轴于点F,连接OP,与BF 交于点G,连接 DG.求四边形 GDEF 面积的最大值.
(3)抛物线上是否存在这样的点 Q，使得 若存在，请求出点Q 的坐标；若不存在，请说明理由.
一、选择题(每小题3分，共 30 分)
题号 1 2 3 4 5
答案 D A B B C
题号 6 7 8 9 10
答案 B B A C D
二、填空题(每小题4分，共 24分)
11.3.52×10 12. 13.3 14.2π—4 15.18
三、解答题(共96 分)
17.解:方程两边同乘x-1,得3+x-1=2x,……………2分
解得x=2………………………………………………………4分
检验:当 x=2时,x-1≠0.
∴x=2是原分式方程的解………………………………6分
18.解:
…………………………5分
……………………………6分
∴原式 …8分
19.(1)证明:∵DE⊥AC,∠ACB=90°,
∴DE∥BC.∴∠EDC=∠BCD.
∵BD=BC,
∴∠CDB=∠BCD.∴∠EDC=∠CDB.
∵DE⊥AC,CF⊥AB,∴∠CED=∠CFD.
在△CED和△CFD中,
∴△CED≌△CFD(AAS),
∴DE=DF.……………………………………………………4分
(2)解:设 BD=x,∴BD=BC=x.
∵AD=1,∴AB=AD+BD=1+x.
又 AC = 3, ∴ 在 Rt△ABC 中, 根 据 勾 股 定 理,得
…9分
20.解：(1)设购进乙种经典读本 x 本，则购进甲种经典读本(x+100)本.
由题意得， ……………………………3分解得 x=900.
经检验，x=900是原分式方程的解，且符合题意.
∴甲种经典读本为900+100=1000(本).……………4分答：购进甲种经典读本 1000本，乙种经典读本 900 本.
(2)设购进甲种经典读本 a 本，则购进乙种经典读本(1300-a)本.
由题意得 …7 分解得 600≤a≤750.
设购进这两种经典读本的总费用为w元.
由题意,得 w=12a+10(1300-a)=2a+13 000. …8分
∵2>0,∴w随a 的增大而增大.
∴当a=600时,w有最小值,为2×600+13 000=14 200.
答：购进这两种经典读本的最低总费用为 14 200 元.
…………………………………………………………………9分
21.解:(1)20 2分
补全的条形统计图如图所示：
……………………………4分
(人)
答：估计该班所在年级 A 类学生的人数是 60. 6 分
(3)由题意,得 A 类 3 人为 1 男 2 女,D 类 3 人为 2 男 1女，列表如下：
D类 A 类 男 女 女
男 (男,男) (男,女) (男,女)
男 (男,男) (男,女) (男,女)
女 (女,男) (女,女) (女,女)
由表可知，共有 9种等可能结果，其中结对互助学习都是男同学有 2 种结果，
∴结对互助学习都是男同学的概率是 .…9分
22.解:如图,作BD⊥CA交CA的延长线于D.………1分
在 Rt△ABD中,∠ABD=45°,
∴AD=BD. 3分
在 Rt△CBD中,∠CBD=60°,
……5分
∵AC=CD-AD,AC=10米,
)(米)…7分
(米).…8分
答：小华在 B 处时距离地面的高度为( 米.…9分
23.解:(1)将 A(1,4)代入 得
∴反比例函数的解析式为 …2分
∵点 B在反比例函数的图象上，
将 A(1,4),B(4,1)代入 得 解得
∴一次函数的解析式为 ………………4分
(2) 如图, 过 点 A 作 直 线AE∥x轴,过 点 C 作 CD⊥DE 于点 D,直线 AB 交 x 轴于点 F.
∵AC⊥AB,∴∠BAC=90°.
∴∠AFO=∠EAF=45°.
∴∠BAE=∠CAD=∠ACD=45°.
∴DA=DC.
∵点 C 在双曲线 上,
∴设点C 的坐标为(n, /n),则.AD=1-n,CD=4- /n,
解得 n=1(舍去)或n=-4.
∴点C的坐标为(-4,-1).……………………………8分
分
24.(1)证明:如图,连接 OC.
∵AB为⊙O的直径,
∴∠ACB=∠OCA+∠OCB=90°,即AC⊥BC.
∵OF⊥BC,∴OF∥AC.
∴∠BOE=∠OAC.
∵OA=OC,
∴∠OCA=∠OAC.
又∠BCD=∠BOE,
∴∠BCD=∠OCA.
∴∠BCD+∠OCB=90°,即∠OCD=90°.
∴OC⊥DC.又OC为⊙O的半径,∴CD为⊙O的切线.………………………4分
(2)解:由(1)知,OF∥AC,又AO=OB,
…6分
∴设 OC=3x,OD=5x,
∴OB=OA=3x. ∴AD=8x.
∵OF∥AC,∴△DOF∽△DAC.
……………8 分
易证)Rt△OCE∽Rt△OFC,
∴⊙O的半径( 10分
25.(1)证明:∵四边形ABCD是正方形,
∴AC⊥BD,OB=OC,∠ABO=∠BCO=45°.
∴∠CON+∠BON=90°.
∵OM⊥ON,
∴∠MOB+∠BON=90°.
∴∠MOB=∠NOC.
∴△MOB≌△NOC(ASA)、
∴OM=ON.………………………………………………………3分
(2)解:OM=kON. 理由如下:如图1,过点 O 作OQ⊥AC交 AB于点Q.
易证△OMQ∽△ONC,
∴OM=kON. 6分
(3)PM=kaPN. 8分
(4)如图2,过点 P 作 PM⊥PN 交 AB 于点 M,连接 MN.
∵∠MPN+∠ABC=180°,
∴M,P,N,B四点共圆.
∴∠BMN=∠BPN.
又∠BPN=∠BAC,
∴∠BMN=∠BAC.
∴NM∥AC.
如图3,过点 P 作 PQ⊥AB 交 AB 于点 Q,交 CD 于点R,作 PT⊥BC 交 BC 于点 T,
则△PMQ∽△GNC,
设 PR=c,则
26.解:(1)设直线 AB 的函数解析式为 y=kx-t(k≠0).
将 A,B两点的坐标(4,0),(1,3)分别代入 y=kx+e中,
得 解得
∴直线 AB的函数解析式为 y=-x+4.
将 x=0 代入 y= -x+4,得 y=4,
∴点C的坐标为(0,4)……………………………………4分
(2)由题可知,抛物线过 O(0,0),A(4,0),B(1.3)三点,
解得
设点 P 的坐标为(
则
∵BF:x=1,∴G(1,-m+4). ∵PE⊥x轴,交直线 y=-x+4于点D,∴D(m,-m+4).
∴yσ=yD.
∴GD∥x轴.
∴四边形 GDEF 为矩形.
∴GD=m-1,GF=-m+4.
∵-1<0,对称轴为直线
∴当 时,S四边形GDEF:最大，为 …9分
(3)存在.如图,连接 OB,过点 B 作 MN⊥y轴,垂足为N,过点 A 作 AM⊥x 轴,两线相交于点 M,在线段 MA上取点H,使MH=BN,连接BH,OH,则OH 与抛物线的交点即为所求点 Q.理由如下：
∵点 B(1,3),
∴BN=1,ON=3.
又点 A(4,0),
∴点 M(4,3).
∴BM=3.
又 MH=BN,∠ONB=∠BMH=90°,
∴△OBN≌△BHM(SAS).
∴OB=HB,且OB⊥HB.
∴∠BOH=45°.
∴OH 与抛物线的交点 Q 即为所求的点.
∵MH=1,
∴点 H(4,2).
∴直线 OH 的解析式为
令
解得 (舍去),
∴点 Q的坐标为( …14分