2024年中考数学模拟试卷六(含答案)

2024年中考数学模拟试卷 (六)
说 明: 1. 全卷满分 150分,考试时间 120 分钟。
2. 本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共三个大题26个小题。
第Ⅰ 卷 选择题(共 30 分)
一、选择题(下列每小题给出的四个选项中，只有一个是符合题意的.每小题3分，共30分)
1.如果a 的相反数是 2024，那么a的值为 ( )
A.2024 B.±2024 D.—2024
2.下列运算正确的是 ( )
C. 3a · 2a=6a
3.下面的四个几何体中，主视图与俯视图相同的是 ( )
4.下列说法错误的是 ( )
A.任意两奇数之和是一个偶数，是必然事件
B.若一组数据0，—1，x，1，2的最大值与最小值的差为4，则x的值一定是—2
C.若一组数据9,9,x,9的方差为0,则 x的值为 9
D.调查某省中学生心理健康现状采用抽样调查
5.如图,直线a∥b,∠3=55°,∠1=80°,则∠2 的度数为 ( )
A.55° B.35°
C.25° D.80°
6.定义一种新运算： a※ 则(—2)※6 的结果为 ( )
A.﹣2 B.2
C.4 D.10
中小学教育资源及组卷应用平台
数学模拟试卷(六) 第 1页(共12 页)
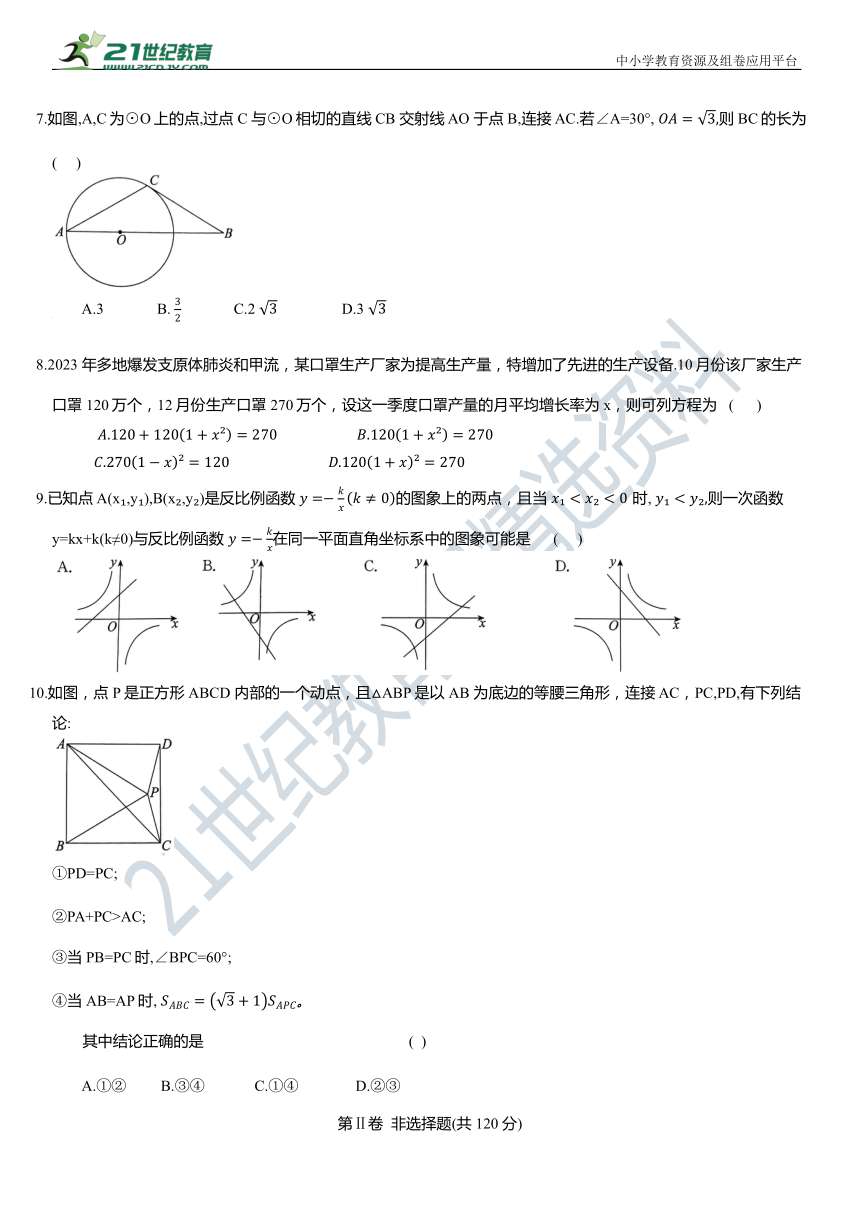
7.如图,A,C为⊙O上的点,过点 C 与⊙O相切的直线CB 交射线 AO 于点B,连接 AC.若∠A=30°, 则 BC的长为 ( )
A.3 B. C.2 D.3
8.2023 年多地爆发支原体肺炎和甲流，某口罩生产厂家为提高生产量，特增加了先进的生产设备.10月份该厂家生产口罩120万个，12月份生产口罩 270万个，设这一季度口罩产量的月平均增长率为x，则可列方程为 ( )
9.已知点A(x ,y ),B(x ,y )是反比例函数 的图象上的两点，且当 时, 则一次函数y=kx+k(k≠0)与反比例函数 在同一平面直角坐标系中的图象可能是 ( )
10.如图，点 P 是正方形ABCD 内部的一个动点，且△ABP是以AB 为底边的等腰三角形，连接 AC，PC,PD,有下列结论:
①PD=PC;
②PA+PC>AC;
③当PB=PC时,∠BPC=60°;
④当AB=AP时,
其中结论正确的是 ( )
A.①② B.③④ C.①④ D.②③
第Ⅱ卷 非选择题(共 120 分)
二、填空题(每小题4分，共24分)
11.分解因式:
12.空气质量指数(AQI)以六大污染物(PM . 、PM 、臭氧、一氧化碳、二氧化硫、二氧化氮)浓度作为分指标.我们经常说的 PM 就是指环境空气中空气动力学当量直径小于等于 0.000 0025 m 的颗粒物，也称细颗粒物.数据 0.000 0025 用科学记数法表示为 .
13.如图，随机闭合3 个开关S ，S ，S 中的一个开关，能使小灯泡 L 发光的概率是 .
14.如果 则 a 的值是 .
15.将正方形 …按如图所示的方式放置，点. ··和点 C ,…分别在直线 y=kx+b(k>0)和 x轴上,已知点. 则 的坐标是 .
16.二次函数 的图象如图所示,有下列结论:①abc>0;②a-b+c<0;③5a+b+c<0;④对于任意实数 m(m≠1),都有 .其中正确结论的序号是 .
三、解答题(要求写出必要的解答步骤或证明过程，共 96 分)
17.(6 分)
计算：
18.(8 分)
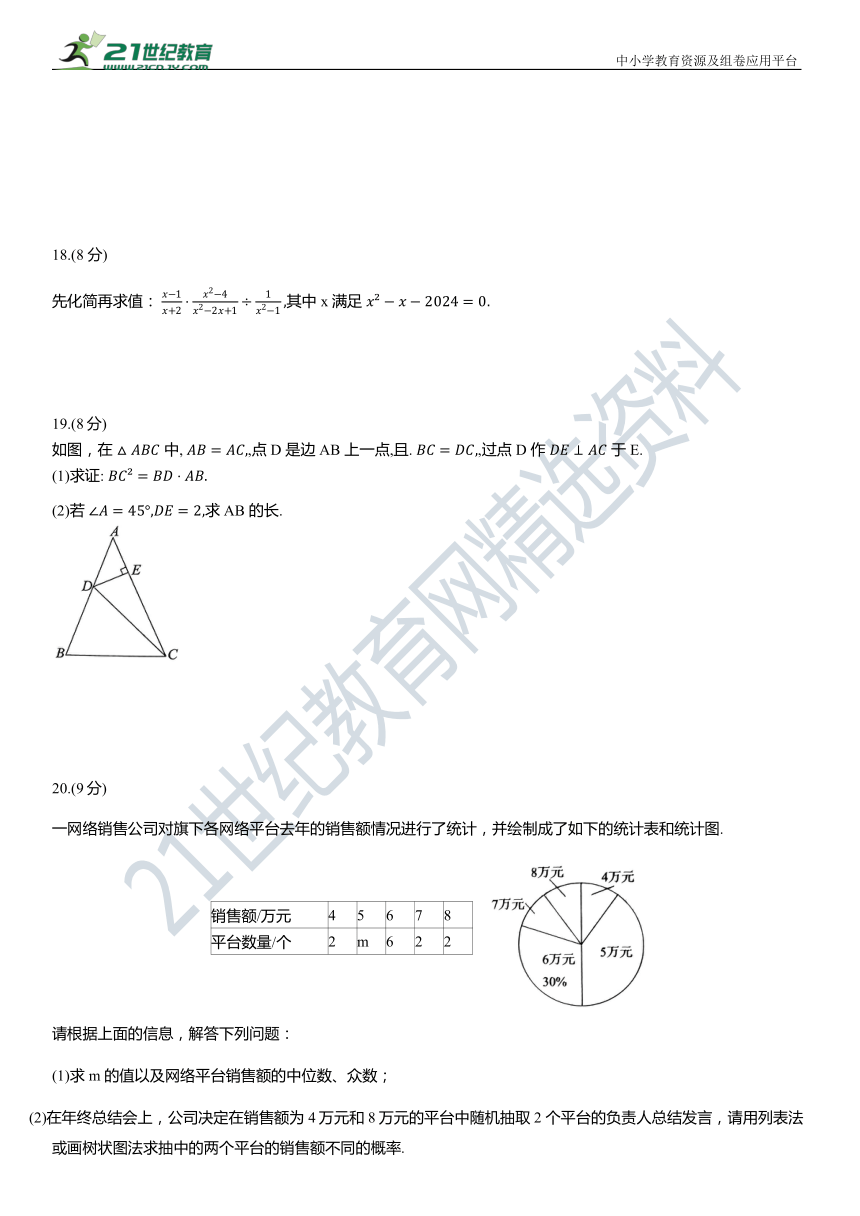
先化简再求值： 其中 x 满足
19.(8分)
如图，在 中, ,点 D 是边AB 上一点,且. ,过点 D 作 于E.
(1)求证:
(2)若 求AB 的长.
20.(9分)
一网络销售公司对旗下各网络平台去年的销售额情况进行了统计，并绘制成了如下的统计表和统计图.
销售额/万元 4 5 6 7 8
平台数量/个 2 m 6 2 2
请根据上面的信息，解答下列问题：
(1)求 m 的值以及网络平台销售额的中位数、众数；
(2)在年终总结会上，公司决定在销售额为4万元和8万元的平台中随机抽取2 个平台的负责人总结发言，请用列表法或画树状图法求抽中的两个平台的销售额不同的概率.
21.(9分)
小刚学了三角函数的知识，就想对自家住的楼进行测量.如图，他操控无人机上升并悬停在距地面50米的点O处，此时在O 处测得楼AB 的顶端 B 处的俯角为 ，人头顶 D处的俯角为 .已知小刚高 1.65 米, ，且A，C，M在一条直线上，点 M到楼底 A 的距离比到小刚的脚C的距离多10 米.求楼 AB 的高度.(结果保留一位小数，参考数据：
22.(10分)
如图，反比例函数 和一次函数 的图象相交于点A(3,a),B(2,b),且一次函数 . 的图象与x轴、y轴分别交于点C，D.
(1)求一次函数的解析式；
(2)当 时，请结合图象直接写出自变量x的取值范围；
(3)连接 AO,BO,求 的面积.
23.(10分)
黑木耳是青川有名的特产，一网络商家将黑木耳的售价定为 90元/千克，该商家每个月可售卖 105千克，获利 2100元，如果每千克黑木耳的售价每上涨2元，该商家每个月就少卖5千克(每千克售价不超过120 元).设每千克黑木耳的售价上涨 2x元(x为正整数)，当月的销售利润为y元.
(1)求 y与x 的函数解析式，并确定自变量 x 的取值范围.
(2)该商家要想每个月获得最大利润，则黑木耳的售价应定为多少元/千克 最大利润又是多少
(3)若每个月的利润不低于 2200 元，请你直接写出售价的取值范围.
24.(10分)
如图，在 中, AD平分 ,交 BC于点D,点O是边 AB 上的点,以点O为圆心，OD长为半径的圆恰好经过点A，交 AC于点E，弦 于点G.
(1)求证:BC是⊙O的切线.
(2)若 求⊙O的半径.
(3)设⊙O与AB 的另一个交点为 H，猜想 AH，AE，CE之间的数量关系，并说明理由.
25.(12分)
如图1,在正方形 ABCD中,点E 是边 BC 上一点,过点 E 向右作 且 ,过点 N 作射线 BC 的垂线,垂足为 H.
(1)求证:
(2)如图2,连接 AC 和CN,AC 与EN 相交于点M,求证:
(3)如图3,点F 是边AB 上一动点,连接 DF,MF,DM,若正方形的边长为4, 求 周长的最小值.
26.(14分)
如图，抛物线 与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
(1)求该抛物线的解析式.
(2)设点 P 是抛物线上的一个动点，是否存在满足 的点 P 若存在，请求出点 P 的坐标；若不存在，请说明理由.
(3)点 Q 是抛物线上的一个动点，当 时，请直接写出点 Q的坐标.
一、选择题(每小题 3 分,共 30分)
题号 1 2 3 4 5
答案 D B A B C
题号 6 7 8 9 10
答案 D A D A C
二、填空题(每小题 4分，共 24分)
11.3a(1+3a)(1-3a) 12.2.5×10 13. /
15.(80,54) 16.②③④
三、解答题(共96分)
17.解:
…5分
=5. 6分
18.解:
)…3分
=(x-2)(x+1)
………………………………………………5分
……………………………………7分
∴原式=2024-2=2022.…………………………………8分
19.(1)证明:∵AB=AC,BC=CD,
∴∠B=∠ACB=∠CDB.
∴△ABC∽△CBD.…………3分
即 ………………………………………4分
(2)解:如图,过点 C 作CF⊥AB 于 F.
∵AB=AC,BC=CD,∠A=45°,
∴∠B=∠ACB=∠CDB=67.5°.
∴∠BCD=45°.
∴∠ACD=∠ACB-∠BCD=22.5°.
∵CF⊥ AB,BC=CD,
∴∠ACD=∠DCF.…………………………………………6分
又 CF⊥AB,DE⊥AC,DE=2,∴DF=DE=2.
∴BD=2DF=4.
∵在Rt△ADE中,∠AED=90°,∠A=45°,DE=2,
………………7分
∴AB=BD+AD=4+2 .………………………………8分
20.解:(1)由题意可知,网络平台的总数为 6÷30%=20(个),∴m=20-2-6-2-2=8(个)…………………………2分将 20 个平台的销售额从小到大排列后处在第 10，11 位的分别是5万元、6万元，
∴中位数是 (万元). 3分
∵平台的销售额出现次数最多的是5 万元，
∴众数是5万元………………………………………………4分
(2)销售额为 4 万元的 2 个平台分别用 A ,A 表示,销售额为 8 万元的 2 个平台分别用 B ，B 表示，抽取的两个平台分别记为第1个、第2个，根据题意列表如下：
第 1 个 第 2 个 A A B B
A 一 (A ,A ) (A ,B ) (A ,B )
A (A ,A ) 一 (A ,B ) (A ,B )
B (B ,A ) (B ,A ) 一 (B ,B )
B (B ,A ) (B ,A ) (B ,B ) 一
由表可知，共有 12 种等可能的结果，其中两个平台销售额不同的结果有 8 种，
∴P(抽中的两个平台的销售额不同) ………9分
21.解:如图,过点 O 作地面 AC 的平行线 EF,延长 AB 交EF 于点 E,延长CD 交 EF 于点 F.
由题意可知,AE⊥EF,CF⊥EF,AE=CF=OM=50米,AM=OE,CM=OF.
∵CD=1.65米, ∴DF=CF-DC=48.35米. 2分
在 Rt△DOF中,∠DFO=90°,∠DOF=73°,
则 (米),
∴OE=AM≈10+14.79=24.79(米).………………5分
在 Rt△BEO中,∠BEO=90°,∠BOE=45°,
则BE=OE≈24.79米, 8分
∴AB=AE-BE≈50-24.79≈25.2(米).
答:楼AB的高度约为25.2米.…………………………9分
22.解:(1)∵A(3,a),B(2,b)在反比例函数 的图象上，∴a=2,b=3,则A(3,2),B(2,3).
∵点 A(3,2),B(2,3)在一次函数. 的图象上， 解得
∴一次函数的解析式为 3分
(2)0(3)如图,作BE⊥x轴于点E,AF⊥x轴于点F.
由(2),知OC=5.
∵B(2,3),A(3,2),
∴BE=3,AF=2.
…10分
23.解:(1)由题意得进价为90-2100÷105=70(元/千克),∴y=(90+2x-70)(105-5x)=-10x +110x+2100.…………………………………………………………………2分
∵每千克售价不超过120元，x为正整数，
解得 0∴自变量 x的取值范围是 0(2)由y= 10x +110x+2100= 10(x 5. 5) +2402.5 可知,当 x=5.5时,函数有最大值 2402.5,但0当x=5或x=6 时, ymax=2400.
∴黑木耳的售价定为90+2×5=100(元/千克)或90+
2×6=102(元/千克)时,利润最大,最大利润是 2400元.…………………………………………………………………7分
(3)黑木耳的售价不低于 92 元/千克，且不超过 110 元/千克，且为偶数……………………………………………10分
24.(1)证明:如图,连接 DO.
∵AD平分∠BAC,∴∠DAC=∠DAO.
∵OA=OD,∴∠ODA=∠DAO.
∴∠ODA=∠DAC.∴OD∥AC.
∴∠BDO=∠C=90°,即OD⊥BC.
又 OD是⊙O的半径,
∴BC是⊙O的切线. 3分
(2)解:如图,连接OE.设OE=x,则OG=OA-AG=x-1.在 Rt△EGO中,由勾股定理,得 即 解得
∴⊙O的半径为 .……6分
(3)AH=AE+2CE.………………………………………7分
理由如下：
如图,过点O作OR⊥AE交AC 于点R.
∴∠ORC=90°,AR=RE.
又∠C=∠ODC=90°,∴四边形 ODCR 是矩形,
∴AH=2OD=AE+2CE.……………………………10分
25.(1)证明:∵四边形 ABCD 是正方形,∴∠ABE=90°.又由题意知,∠NHE=90°,∠AEN=90°,
∴∠BAE+∠AEB=90°,∠AEB+∠NEH=90°.
∴∠BAE=∠NEH.
又AE=EN,∴△ABE≌△EHN(AAS).………4分
(2)证明:由(1)知,AB=BC=EH=EC+CH=BE+CE,BE=NH,
∴NH=CH.∴∠NCH=45°.
∵AC是正方形 ABCD 的对角线,∴∠ACB=45°.
∴∠ACN=∠AEN=90°.
又∠AME=∠NMC,∴△AME∽△NMC.
即AM·CM=EM·NM.…8分
(3)解:如图,过点 M 作 GM'⊥BC,交 BC 于 点 M',交AD 于点 G,作点 D 关于直线 AB 的对称点 D',连接 D'M,则(D'M+DM)就是△DFM周长的最小值.作 MI⊥CD于点Ⅰ.
由题意可得四边形 MM'CI 是正方形，四边形 DGMI 是矩形.又CD=4,CM= , ∴DG=IM=1. ∴GM=DI=3,
在Rt△D'MG 中,
∴△DFM周长的最小值为
………………………………………………………………12分
26.解:(1)∵抛物线 与x 轴交于 A(-3,0),B(1,0)两点,
解得
∴抛物线的解析式为 ………………4分
(2)存在.设点 P 的坐标为(x,y).
由题意，得 ∴y=±2.
当 y=2 时, 解得
当y=-2时, 解得
∴存在满足S△PAB=4的点 P，点 P 的坐标为
2)或( 或 或
10分
(3)Q(-4,5)或(-2,-3). 14分