7.3.2随机变量的方差 课件(共22张PPT)-2023-2024学年高二下学期数学人教A版(2019)选择性必修第三册
文档属性
| 名称 | 7.3.2随机变量的方差 课件(共22张PPT)-2023-2024学年高二下学期数学人教A版(2019)选择性必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 55.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-19 22:32:24 | ||
图片预览








文档简介
(共22张PPT)
7.3.2 离散型随机变量的数字特征(方差)
1.离散型随机变量的数学期望
2.数学期望的性质
数学期望是反映离散型随机变量的平均水平
4.样本方差
3.特殊分布----两点分布的均值
若随机变量X服从两点分布,则
温故知新
设在一组数据,是数据的平均数,那么
叫做这组数据的方差.
4.样本方差
叫做这组数据的方差.
温故知新
设在一组数据,是数据的平均数,那么
各个数据与样本平均数的
偏差平方的平均值
思考:你能否类比上式归纳得到随机变量X的方差?
各个数据与样本平均数的偏差平方的加权平均值
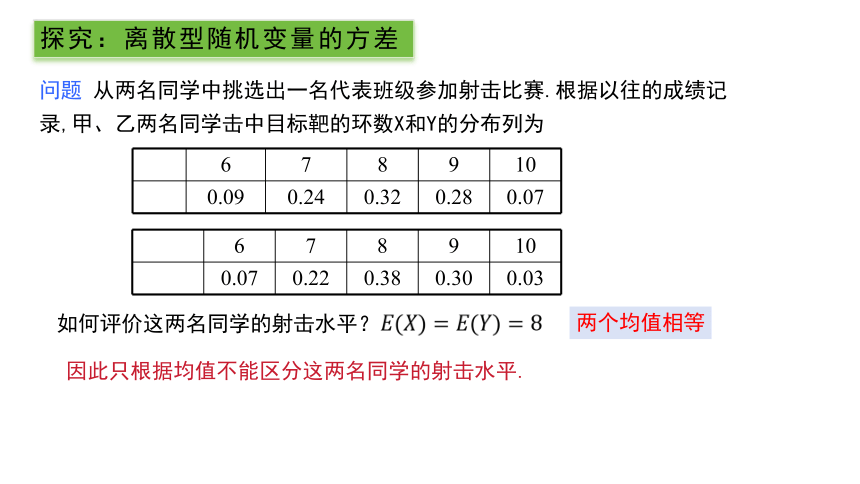
如何评价这两名同学的射击水平?
因此只根据均值不能区分这两名同学的射击水平.
问题 从两名同学中挑选出一名代表班级参加射击比赛.根据以往的成绩记录,甲、乙两名同学击中目标靶的环数X和Y的分布列为
两个均值相等
探究:离散型随机变量的方差
6 7 8 9 10
0.09 0.24 0.32 0.28 0.07
6 7 8 9 10
0.07 0.22 0.38 0.30 0.03
探究:离散型随机变量的方差
比较两个图形,哪一名同学的射击成绩更稳定
除平均中靶环数以外,还要考虑稳定性,即击中环数的离散程度.
乙同学的射击成绩更稳定
下图分别是X和Y的概率分布图.
Y
P
10
9
8
7
0
6
X
P
10
9
8
7
0
6
如何量化这个衡量标准?
如何定量刻画离散型随机变量取值的离散程度?
样本的方差:
随机变量的方差
(1)样本的离散程度是用哪个量刻画的?
(2)能否用一个与样本方差类似的量来刻画随机变量的稳定性呢?
偏差平方关于取值概率的加权平均
探究:离散型随机变量的方差
若离散型随机变量X的分布列为:
随机变量X的方差为:
X x1 x2 … xi … xn
P p1 p2 … pi … pn
随机变量的方差和标准差都可度量随机变量取值与其均值的偏离程度,反映随机变量取值的离散程度.
随机变量X的标准差为:
概念:离散型随机变量的方差
6 7 8 9 10
0.09 0.24 0.32 0.28 0.07
6 7 8 9 10
0.07 0.22 0.38 0.30 0.03
D(X)>D(Y),即乙同学的射击成绩相对更稳定
下面用两名同学射击成绩的的方差和标准差来刻画他们射击成绩的稳定性
离散型随机变量的方差
例6.投资A,B两种股票,每股收益的分布列分别如表所示.
(1)投资哪种股票的期望收益大? (2)投资哪种股票的风险高?
解:(1)股票A的期望收益为E(X)=( 1)×0.1+0×0.3+2×0.6=1.1,
股票B的期望收益为E(Y)=0×0.3+1×0.4+2×0.3=1.
∵E(X)>E(Y),∴投资股票A的期望收益较大.
(2)股票A的收益的方差为D(X)=( 1)2×0.1+02×0.3+22×0.6 1.12=1.29,
股票B的收益的方差为D(Y)=02×0.3+12×0.4+22×0.3 12=0.6.
∵E(X)和E(Y)相差不大,但D(X)>D(Y),∴投资A股票比投资B股票的风险高.
离散型随机变量的方差
离散型随机变量的方差的性质
数学含义不一定成立
离散型随机变量的方差的性质
离散型随机变量X加上一个常数,方差会有怎样变化?离散型随机变量X乘以一个常数,方差又有怎样的变化?它们和期望的性质有什么不同?
离散型随机变量X加上一个常数b,仅仅使X的值产生一个平移,不改变X与其均值的离散程度,方差保持不变,即D(X+b)= D(X)
而离散型随机变量X乘以一个常数a,其方差变为原方差的a2倍,即D(aX)=a2D(X)
性质2:
与无关
离散型随机变量的方差的性质
练习 已知的分布列如表所示:
(1)求的分布列;
(2)计算的方差;
(3)若,求的均值和方差.
离散型随机变量的方差的性质
(2)计算的方差;
离散型随机变量的方差的性质
(3)若,求的均值和方差.
性质2:
与无关
方差性质应用的关注点
(1)公式:D(aX+b)=a2D(X).
(2)优势:既避免了求随机变量Y=aX+b的分布列,又避免了涉及大数的计算,从而简化了计算过程.
常见概率分布的方差
若服从两点(0-1)分布,
X 1 0
P p 1-p
则D(X)=p(1-p).
跟踪训练 某投资公司对以下两个项目进行前期市场调研.
项目A:通信设备.根据调研,投资到该项目上,所有可能结果为获利40%、亏损20%、不赔不赚,且这三种情况发生的概率分别为 , ,a.
项目B:新能源汽车.根据调研,投资到该项目上,所有可能结果为获利30%、亏损10%,且这两种情况发生的概率分别为b,c.
经测算,当投入A,B两个项目的资金相等时,它们所获得的平均收益(即均值)也相等.
(1)求a,b,c的值;
(2)若将100万元全部投资其中一个项目,请你从投资回报稳定性的角度考虑,为投资公司选择一个合理的项目,并说明理由.
离散型随机变量数字特征的应用
离散型随机变量数字特征的应用
设投到项目A,B的资金都为x万元,变量X1和X2分别表示投资项目A和B所获得的利润,则X1和X2的分布列分别为
X2 0.3x -0.1x
P b c
(1)求a,b,c的值;
E(X2)=0.3bx-0.1cx,
因为E(X1)=E(X2),
所以0.3bx-0.1cx=0.2x,
即0.3b-0.1c=0.2. ①
又b+c=1, ②
离散型随机变量数字特征的应用
离散型随机变量数字特征的应用
(2)若将100万元全部投资其中一个项目,请你从投资回报稳定性的角度考虑,为投资公司选择一个合理的项目,并说明理由.
选择项目B.理由如下:
当投入100万元资金时,由(1)知x=100,
所以E(X1)=E(X2)=20,
因为E(X1)=E(X2),D(X1)>D(X2),说明虽然项目A和项目B的平均收益相等,但项目B更稳妥,所以从投资回报稳定性的角度考虑,建议该投资公司选择项目B.
1.离散型随机变量取值的方差、标准差
3.求离散型随机变量X 的方差、标准差的一般步骤:
①理解X 的意义,写出X 可能取的全部值;
②求X取各个值的概率,写出分布列;
③根据分布列,由期望的定义求出 E(X );
4.若 X 服从两点分布,则
④根据方差、标准差的定义求出
方差:
标准差:
2.方差的性质:
课堂小结
谢谢
7.3.2 离散型随机变量的数字特征(方差)
1.离散型随机变量的数学期望
2.数学期望的性质
数学期望是反映离散型随机变量的平均水平
4.样本方差
3.特殊分布----两点分布的均值
若随机变量X服从两点分布,则
温故知新
设在一组数据,是数据的平均数,那么
叫做这组数据的方差.
4.样本方差
叫做这组数据的方差.
温故知新
设在一组数据,是数据的平均数,那么
各个数据与样本平均数的
偏差平方的平均值
思考:你能否类比上式归纳得到随机变量X的方差?
各个数据与样本平均数的偏差平方的加权平均值
如何评价这两名同学的射击水平?
因此只根据均值不能区分这两名同学的射击水平.
问题 从两名同学中挑选出一名代表班级参加射击比赛.根据以往的成绩记录,甲、乙两名同学击中目标靶的环数X和Y的分布列为
两个均值相等
探究:离散型随机变量的方差
6 7 8 9 10
0.09 0.24 0.32 0.28 0.07
6 7 8 9 10
0.07 0.22 0.38 0.30 0.03
探究:离散型随机变量的方差
比较两个图形,哪一名同学的射击成绩更稳定
除平均中靶环数以外,还要考虑稳定性,即击中环数的离散程度.
乙同学的射击成绩更稳定
下图分别是X和Y的概率分布图.
Y
P
10
9
8
7
0
6
X
P
10
9
8
7
0
6
如何量化这个衡量标准?
如何定量刻画离散型随机变量取值的离散程度?
样本的方差:
随机变量的方差
(1)样本的离散程度是用哪个量刻画的?
(2)能否用一个与样本方差类似的量来刻画随机变量的稳定性呢?
偏差平方关于取值概率的加权平均
探究:离散型随机变量的方差
若离散型随机变量X的分布列为:
随机变量X的方差为:
X x1 x2 … xi … xn
P p1 p2 … pi … pn
随机变量的方差和标准差都可度量随机变量取值与其均值的偏离程度,反映随机变量取值的离散程度.
随机变量X的标准差为:
概念:离散型随机变量的方差
6 7 8 9 10
0.09 0.24 0.32 0.28 0.07
6 7 8 9 10
0.07 0.22 0.38 0.30 0.03
D(X)>D(Y),即乙同学的射击成绩相对更稳定
下面用两名同学射击成绩的的方差和标准差来刻画他们射击成绩的稳定性
离散型随机变量的方差
例6.投资A,B两种股票,每股收益的分布列分别如表所示.
(1)投资哪种股票的期望收益大? (2)投资哪种股票的风险高?
解:(1)股票A的期望收益为E(X)=( 1)×0.1+0×0.3+2×0.6=1.1,
股票B的期望收益为E(Y)=0×0.3+1×0.4+2×0.3=1.
∵E(X)>E(Y),∴投资股票A的期望收益较大.
(2)股票A的收益的方差为D(X)=( 1)2×0.1+02×0.3+22×0.6 1.12=1.29,
股票B的收益的方差为D(Y)=02×0.3+12×0.4+22×0.3 12=0.6.
∵E(X)和E(Y)相差不大,但D(X)>D(Y),∴投资A股票比投资B股票的风险高.
离散型随机变量的方差
离散型随机变量的方差的性质
数学含义不一定成立
离散型随机变量的方差的性质
离散型随机变量X加上一个常数,方差会有怎样变化?离散型随机变量X乘以一个常数,方差又有怎样的变化?它们和期望的性质有什么不同?
离散型随机变量X加上一个常数b,仅仅使X的值产生一个平移,不改变X与其均值的离散程度,方差保持不变,即D(X+b)= D(X)
而离散型随机变量X乘以一个常数a,其方差变为原方差的a2倍,即D(aX)=a2D(X)
性质2:
与无关
离散型随机变量的方差的性质
练习 已知的分布列如表所示:
(1)求的分布列;
(2)计算的方差;
(3)若,求的均值和方差.
离散型随机变量的方差的性质
(2)计算的方差;
离散型随机变量的方差的性质
(3)若,求的均值和方差.
性质2:
与无关
方差性质应用的关注点
(1)公式:D(aX+b)=a2D(X).
(2)优势:既避免了求随机变量Y=aX+b的分布列,又避免了涉及大数的计算,从而简化了计算过程.
常见概率分布的方差
若服从两点(0-1)分布,
X 1 0
P p 1-p
则D(X)=p(1-p).
跟踪训练 某投资公司对以下两个项目进行前期市场调研.
项目A:通信设备.根据调研,投资到该项目上,所有可能结果为获利40%、亏损20%、不赔不赚,且这三种情况发生的概率分别为 , ,a.
项目B:新能源汽车.根据调研,投资到该项目上,所有可能结果为获利30%、亏损10%,且这两种情况发生的概率分别为b,c.
经测算,当投入A,B两个项目的资金相等时,它们所获得的平均收益(即均值)也相等.
(1)求a,b,c的值;
(2)若将100万元全部投资其中一个项目,请你从投资回报稳定性的角度考虑,为投资公司选择一个合理的项目,并说明理由.
离散型随机变量数字特征的应用
离散型随机变量数字特征的应用
设投到项目A,B的资金都为x万元,变量X1和X2分别表示投资项目A和B所获得的利润,则X1和X2的分布列分别为
X2 0.3x -0.1x
P b c
(1)求a,b,c的值;
E(X2)=0.3bx-0.1cx,
因为E(X1)=E(X2),
所以0.3bx-0.1cx=0.2x,
即0.3b-0.1c=0.2. ①
又b+c=1, ②
离散型随机变量数字特征的应用
离散型随机变量数字特征的应用
(2)若将100万元全部投资其中一个项目,请你从投资回报稳定性的角度考虑,为投资公司选择一个合理的项目,并说明理由.
选择项目B.理由如下:
当投入100万元资金时,由(1)知x=100,
所以E(X1)=E(X2)=20,
因为E(X1)=E(X2),D(X1)>D(X2),说明虽然项目A和项目B的平均收益相等,但项目B更稳妥,所以从投资回报稳定性的角度考虑,建议该投资公司选择项目B.
1.离散型随机变量取值的方差、标准差
3.求离散型随机变量X 的方差、标准差的一般步骤:
①理解X 的意义,写出X 可能取的全部值;
②求X取各个值的概率,写出分布列;
③根据分布列,由期望的定义求出 E(X );
4.若 X 服从两点分布,则
④根据方差、标准差的定义求出
方差:
标准差:
2.方差的性质:
课堂小结
谢谢
