《4.2.1指数函数的概念》课件(共24张PPT)高中数学人教A版(2019)必修第一册
文档属性
| 名称 | 《4.2.1指数函数的概念》课件(共24张PPT)高中数学人教A版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 15.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-20 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
高中数学人教A版必修第一册
第四章《指数函数与对数函数》
§4.2.1 指数函数的概念
A版
自主学习成果分享
上一章学习了函数的概念和基本性质,通过对幂函数的研究,了解了研究一类函数的过程和方法:
背景——概念——图象与性质——应用
下面我们继续研究其他类型的基本初等函数.
传说古印度的宰相西萨发明了国际象棋,国王很喜欢这个游戏,决定奖赏他,表示可以满足他任何一个要求。宰相微笑着说出了他的要求:在他的棋盘上摆满麦粒,第1格放2粒,第2格放4粒,第3格放8粒……每一小格的麦粒数量都是前一格的2倍,直至所有格子都摆满。
《庄子·天下篇》中写道:
“一尺之棰,日取之半,万世不竭”
当生物死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.按照上述变化规律,生物体内碳14含量与死亡年数之间有怎样的关系?
自主学习成果分享
请同学们在小组内相互交流,解决自主学习任务单中遇到的困惑,或者分享自己微课学习中的收获.
自主学习成果分享
传说古印度的宰相西萨发明了国际象棋,国王很喜欢这个游戏,决定奖赏他,表示可以满足他任何一个要求。宰相微笑着说出了他的要求:在他的棋盘上摆满麦粒,第1格放2粒,第2格放4粒,第3格放8粒……每一小格的麦粒数量都是前一格的2倍,直至所有格子都摆满。
格子编号 1 2 3 4 5 …… 64
小麦粒数 ……
“一尺之棰,日取之半,万世不竭”
《庄子·天下篇》中写道:
当生物死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.按照上述变化规律,生物体内碳14含量与死亡年数之间有怎样的关系?
截取次数 1 2 3 4 5 ……
木锤剩余量 ……
死亡年数 1 2 3 4 ……
内碳14含量 ……
自主学习成果分享
创设情境 探究模型
脱贫攻坚战的伟大胜利,标志着我国现行标准下9899万农村贫困人口全部脱贫,832个贫困县全部摘帽.存在了34年的国务院扶贫办,也正式更名为国家乡村振兴局。
创设情境 探究模型
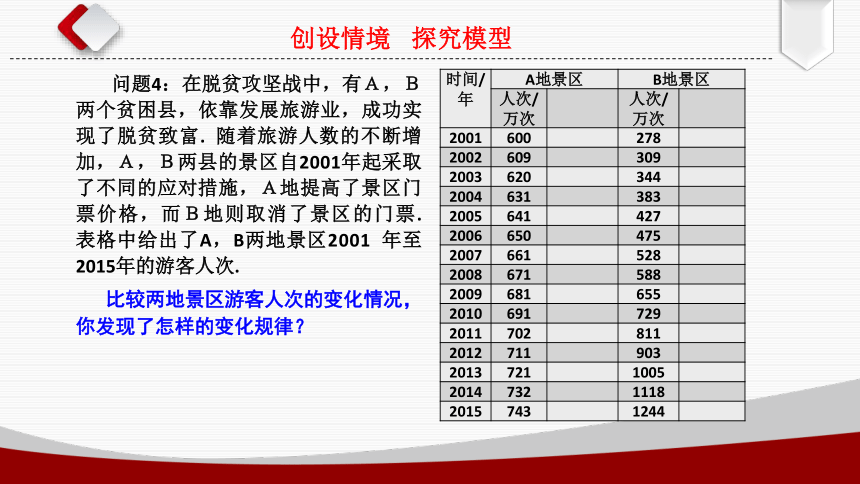
比较两地景区游客人次的变化情况,你发现了怎样的变化规律?
问题4:在脱贫攻坚战中,有A,B两个贫困县,依靠发展旅游业,成功实现了脱贫致富. 随着旅游人数的不断增加,A,B两县的景区自2001年起采取了不同的应对措施,A地提高了景区门票价格,而B地则取消了景区的门票. 表格中给出了A,B两地景区2001 年至2015年的游客人次.
时间/年 A地景区 B地景区 人次/ 万次 人次/万次
2001 600 278
2002 609 309
2003 620 344
2004 631 383
2005 641 427
2006 650 475
2007 661 528
2008 671 588
2009 681 655
2010 691 729
2011 702 811
2012 711 903
2013 721 1005
2014 732 1118
2015 743 1244
创设情境 探究模型
时间/年 A地景区 B地景区 人次/万次 人次/万次
2001 600 278
2002 609 309
2003 620 344
2004 631 383
2005 641 427
2006 650 475
2007 661 528
2008 671 588
2009 681 655
2010 691 729
2011 702 811
2012 711 903
2013 721 1005
2014 732 1118
2015 743 1244
年增加量
/万次
9
11
11
10
9
11
10
10
10
11
9
10
11
11
A景区的游客人次每年增加量都约为10万人次.
以2001年游客人次为基数,设经过x年后的游客人次为y万次,则 x和y之间的函数关系是:
思考1.从图象看,A地景区游客人次的变化近似呈线性增长.线性增长的规律能用表格中的数据体现出来吗?这种规律用函数关系如何刻画呢?
年增加量
/万次
31
35
39
44
48
53
60
67
74
82
92
102
113
126
增加量为常数的变化方式,称为线性增长.
合作交流 互助互学
时间/年 A地景区 B地景区 人次/万次 人次/万次
2001 600 278
2002 609 309
2003 620 344
2004 631 383
2005 641 427
2006 650 475
2007 661 528
2008 671 588
2009 681 655
2010 691 729
2011 702 811
2012 711 903
2013 721 1005
2014 732 1118
2015 743 1244
年增加量
/万次
9
11
11
10
9
11
10
10
10
11
9
10
11
11
年增加量
/万次
31
35
39
44
48
53
60
67
74
82
92
102
113
126
1.111510791367
1.113268608414
1.113372093023
1.114882506527
1.112412177986
1.111578947368
1.113636363636
1.113945578231
1.112977099237
1.112482853224
1.113440197287
1.112956810631
1.112437810945
1.112701252236
思考2.年增加量是对相邻两年的游客人次做减法得到的,能否通过对B地景区每年的游客人次做其它运算,发现游客人次的变化规律呢 请你试一试.
合作交流 互助互学
增长率
增加量
增长前的量
做除法运算,B景区从2002年开始,每年游客人次约为上一年的1.11倍.
(年增长率约为0.11)
时间/年 A地景区 B地景区 人次/万次 人次/万次
2001 600 278
2002 609 309
2003 620 344
2004 631 383
2005 641 427
2006 650 475
2007 661 528
2008 671 588
2009 681 655
2010 691 729
2011 702 811
2012 711 903
2013 721 1005
2014 732 1118
2015 743 1244
年增加量
/万次
9
11
11
10
9
11
10
10
10
11
9
10
11
11
年增加量
/万次
31
35
39
44
48
53
60
67
74
82
92
102
113
126
1.111510791367
1.113268608414
1.113372093023
1.114882506527
1.112412177986
1.111578947368
1.113636363636
1.113945578231
1.112977099237
1.112482853224
1.113440197287
1.112956810631
1.112437810945
1.112701252236
合作交流 互助互学
思考3.请用函数关系描述B地景区游客人次的变化规律.
以2001年游客人次为基数, 设经过 x 年后B地景区的游客人次约为2001年的 y 倍,则
令
p 表示年增长率
增加量、增长率是刻画事物变化规律的两个重要的量.
B地
增长率为常数的变化方式,称为指数增长.
合作交流 互助互学
思考3.请用函数关系描述B地景区游客人次的变化规律.
以2001年游客人次为基数, 设经过 x 年后B地景区的游客人次约为2001年的 y 倍,则
令
p 表示年增长率
当生物死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.按照上述变化规律,生物体内碳14含量与死亡年数之间有怎样的关系?
衰减率为常数的变化
方式,称为指数衰减
如果把刚死亡的生物体内碳14含量看成1个单位,设死亡年数为 x,死亡的生物体内碳14含量为 y
合作交流 互助互学
抽象特征 形成概念
观察得到的这四个函数,它们有什么共同特征?
1.结构特点:
指数幂形式
自变量在指数位置
底数是常量
2.反映的规律:
变化率(增长率、衰减率)是常数
传说古印度的宰相西萨发明了国际象棋,国王很喜欢这个游戏,决定奖赏他,表示可以满足他任何一个要求。宰相微笑着说出了他的要求:在他的棋盘上摆满麦粒,第1格放2粒,第2格放4粒,第3格放8粒……每一小格的麦粒数量都是前一格的2倍,直至所有格子都摆满。
格子编号 1 2 3 4 5 …… 64
小麦粒数 ……
“一尺之棰,日取之半,万世不竭”
《庄子·天下篇》中写道:
截取次数 1 2 3 4 5 ……
木锤剩余量 ……
所以规定:
抽象特征 形成概念
若将函数的定义域扩充到实数集,即,对底数有什么要求?
a < 0 时,
a = 0 时,
a = 1 时,
指数函数的定义
一般地,函数叫做指数函数(exponential function),其中是自变量,函数的定义域是R.
抽象特征 形成概念
例1.判断下列函数是否是指数函数.
①
②
③
⑥
⑤
④
⑧
⑦
【规律方法】
1.在指数函数定义的表达式中,要牢牢抓住三点:
底数是大于0且不等于1的常数;
指数函数的自变量必须位于指数的位置上;
ax的系数必须为1.
概念应用 加深理解
1. 函数是指数函数,则.
2.已知指数函数的图象过点,则______.
跟进练习:
概念应用 加深理解
【规律方法】
2.求指数函数的解析式常用待定系数法.
例2. 在问题4中,如果平均每位游客出游一次可给当地带来1000元门票之外的收入,A地景区的门票价格为150元,比较这15年间A,B两地旅游收入变化情况.
利用图象中的数据得出:
当x=0时,f(0)-g(0)=412 000(万元)=41.2(亿元).
当x≈10.22时,f(10.22)≈g(10.22).
当x=14时,g(14)-f (14)≈34.73 (亿元).
当x<10.22时,f(x)>g(x).
当x>10.22时,f(x)f(x)=1150(600+10x) ,
解:设经过x年,游客给A、B两地带来的收入
分别为f(x),g(x),则
概念应用 加深理解
g(x)=1000×278×1.11x .
这说明:
在2001年,游客给A地带来的收入比B地多41.2亿元;
随后的10年,游客给A地带来的收入仍高于B地,但g(x)比f(x)增长的速度快,大约2011年2月某个时刻就有f(x)=g(x),这时游客给A地带来的收入和B地差不多;
此后,游客给B地带来的收入高于A地了,由于g(x)增长的速度越来越快,而f(x)增长的速度不变,到2015年,游客给B地带来的收入已经高于了A地约34.73亿元了.
在实际问题中,经常会遇到如g(x)=1000×278×1.11x
指数增长模型:设原有量为N,每次的增长率为p,则经过x次增长,该量增长到y ,则y=N(1+p)x(x∈N).
指数衰减模型:设原有量为N,每次的衰减率为p,则经过x次减少,该量衰减到y ,则y =N (1-p) x(x ∈N).
形如 的函数,在,称为指数型函数. 这是刻画指数增长或指数衰减变化规律的非常有用的函数模型.
概念应用 加深理解
跟进练习:某地2012年底人口为500万,人均住房面积为6 m2,若该地区的人口年平均增长率为1%,要使2022年底该地区人均住房面积至少为7 m2,平均每年新增住房面积至少为多少万m2?
(精确到1万m2,参考数据:1.019≈1.093 7,1.0110≈1.104 6,1.0111≈1.115 7)
概念应用 加深理解
本节课你学到了那些知识?在探究规律和形成概念的过程中,用到了哪些数学思想方法?
课堂总结 提炼升华
函数概念
实际问题
数学抽象
数形结合思想
变化率是常数
从特殊到一般
数学运算
指数函数
一个概念:
一类函数:
核心素养:
数学思想:
高中数学人教A版必修第一册
第四章《指数函数与对数函数》
§4.2.1 指数函数的概念
A版
自主学习成果分享
上一章学习了函数的概念和基本性质,通过对幂函数的研究,了解了研究一类函数的过程和方法:
背景——概念——图象与性质——应用
下面我们继续研究其他类型的基本初等函数.
传说古印度的宰相西萨发明了国际象棋,国王很喜欢这个游戏,决定奖赏他,表示可以满足他任何一个要求。宰相微笑着说出了他的要求:在他的棋盘上摆满麦粒,第1格放2粒,第2格放4粒,第3格放8粒……每一小格的麦粒数量都是前一格的2倍,直至所有格子都摆满。
《庄子·天下篇》中写道:
“一尺之棰,日取之半,万世不竭”
当生物死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.按照上述变化规律,生物体内碳14含量与死亡年数之间有怎样的关系?
自主学习成果分享
请同学们在小组内相互交流,解决自主学习任务单中遇到的困惑,或者分享自己微课学习中的收获.
自主学习成果分享
传说古印度的宰相西萨发明了国际象棋,国王很喜欢这个游戏,决定奖赏他,表示可以满足他任何一个要求。宰相微笑着说出了他的要求:在他的棋盘上摆满麦粒,第1格放2粒,第2格放4粒,第3格放8粒……每一小格的麦粒数量都是前一格的2倍,直至所有格子都摆满。
格子编号 1 2 3 4 5 …… 64
小麦粒数 ……
“一尺之棰,日取之半,万世不竭”
《庄子·天下篇》中写道:
当生物死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.按照上述变化规律,生物体内碳14含量与死亡年数之间有怎样的关系?
截取次数 1 2 3 4 5 ……
木锤剩余量 ……
死亡年数 1 2 3 4 ……
内碳14含量 ……
自主学习成果分享
创设情境 探究模型
脱贫攻坚战的伟大胜利,标志着我国现行标准下9899万农村贫困人口全部脱贫,832个贫困县全部摘帽.存在了34年的国务院扶贫办,也正式更名为国家乡村振兴局。
创设情境 探究模型
比较两地景区游客人次的变化情况,你发现了怎样的变化规律?
问题4:在脱贫攻坚战中,有A,B两个贫困县,依靠发展旅游业,成功实现了脱贫致富. 随着旅游人数的不断增加,A,B两县的景区自2001年起采取了不同的应对措施,A地提高了景区门票价格,而B地则取消了景区的门票. 表格中给出了A,B两地景区2001 年至2015年的游客人次.
时间/年 A地景区 B地景区 人次/ 万次 人次/万次
2001 600 278
2002 609 309
2003 620 344
2004 631 383
2005 641 427
2006 650 475
2007 661 528
2008 671 588
2009 681 655
2010 691 729
2011 702 811
2012 711 903
2013 721 1005
2014 732 1118
2015 743 1244
创设情境 探究模型
时间/年 A地景区 B地景区 人次/万次 人次/万次
2001 600 278
2002 609 309
2003 620 344
2004 631 383
2005 641 427
2006 650 475
2007 661 528
2008 671 588
2009 681 655
2010 691 729
2011 702 811
2012 711 903
2013 721 1005
2014 732 1118
2015 743 1244
年增加量
/万次
9
11
11
10
9
11
10
10
10
11
9
10
11
11
A景区的游客人次每年增加量都约为10万人次.
以2001年游客人次为基数,设经过x年后的游客人次为y万次,则 x和y之间的函数关系是:
思考1.从图象看,A地景区游客人次的变化近似呈线性增长.线性增长的规律能用表格中的数据体现出来吗?这种规律用函数关系如何刻画呢?
年增加量
/万次
31
35
39
44
48
53
60
67
74
82
92
102
113
126
增加量为常数的变化方式,称为线性增长.
合作交流 互助互学
时间/年 A地景区 B地景区 人次/万次 人次/万次
2001 600 278
2002 609 309
2003 620 344
2004 631 383
2005 641 427
2006 650 475
2007 661 528
2008 671 588
2009 681 655
2010 691 729
2011 702 811
2012 711 903
2013 721 1005
2014 732 1118
2015 743 1244
年增加量
/万次
9
11
11
10
9
11
10
10
10
11
9
10
11
11
年增加量
/万次
31
35
39
44
48
53
60
67
74
82
92
102
113
126
1.111510791367
1.113268608414
1.113372093023
1.114882506527
1.112412177986
1.111578947368
1.113636363636
1.113945578231
1.112977099237
1.112482853224
1.113440197287
1.112956810631
1.112437810945
1.112701252236
思考2.年增加量是对相邻两年的游客人次做减法得到的,能否通过对B地景区每年的游客人次做其它运算,发现游客人次的变化规律呢 请你试一试.
合作交流 互助互学
增长率
增加量
增长前的量
做除法运算,B景区从2002年开始,每年游客人次约为上一年的1.11倍.
(年增长率约为0.11)
时间/年 A地景区 B地景区 人次/万次 人次/万次
2001 600 278
2002 609 309
2003 620 344
2004 631 383
2005 641 427
2006 650 475
2007 661 528
2008 671 588
2009 681 655
2010 691 729
2011 702 811
2012 711 903
2013 721 1005
2014 732 1118
2015 743 1244
年增加量
/万次
9
11
11
10
9
11
10
10
10
11
9
10
11
11
年增加量
/万次
31
35
39
44
48
53
60
67
74
82
92
102
113
126
1.111510791367
1.113268608414
1.113372093023
1.114882506527
1.112412177986
1.111578947368
1.113636363636
1.113945578231
1.112977099237
1.112482853224
1.113440197287
1.112956810631
1.112437810945
1.112701252236
合作交流 互助互学
思考3.请用函数关系描述B地景区游客人次的变化规律.
以2001年游客人次为基数, 设经过 x 年后B地景区的游客人次约为2001年的 y 倍,则
令
p 表示年增长率
增加量、增长率是刻画事物变化规律的两个重要的量.
B地
增长率为常数的变化方式,称为指数增长.
合作交流 互助互学
思考3.请用函数关系描述B地景区游客人次的变化规律.
以2001年游客人次为基数, 设经过 x 年后B地景区的游客人次约为2001年的 y 倍,则
令
p 表示年增长率
当生物死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.按照上述变化规律,生物体内碳14含量与死亡年数之间有怎样的关系?
衰减率为常数的变化
方式,称为指数衰减
如果把刚死亡的生物体内碳14含量看成1个单位,设死亡年数为 x,死亡的生物体内碳14含量为 y
合作交流 互助互学
抽象特征 形成概念
观察得到的这四个函数,它们有什么共同特征?
1.结构特点:
指数幂形式
自变量在指数位置
底数是常量
2.反映的规律:
变化率(增长率、衰减率)是常数
传说古印度的宰相西萨发明了国际象棋,国王很喜欢这个游戏,决定奖赏他,表示可以满足他任何一个要求。宰相微笑着说出了他的要求:在他的棋盘上摆满麦粒,第1格放2粒,第2格放4粒,第3格放8粒……每一小格的麦粒数量都是前一格的2倍,直至所有格子都摆满。
格子编号 1 2 3 4 5 …… 64
小麦粒数 ……
“一尺之棰,日取之半,万世不竭”
《庄子·天下篇》中写道:
截取次数 1 2 3 4 5 ……
木锤剩余量 ……
所以规定:
抽象特征 形成概念
若将函数的定义域扩充到实数集,即,对底数有什么要求?
a < 0 时,
a = 0 时,
a = 1 时,
指数函数的定义
一般地,函数叫做指数函数(exponential function),其中是自变量,函数的定义域是R.
抽象特征 形成概念
例1.判断下列函数是否是指数函数.
①
②
③
⑥
⑤
④
⑧
⑦
【规律方法】
1.在指数函数定义的表达式中,要牢牢抓住三点:
底数是大于0且不等于1的常数;
指数函数的自变量必须位于指数的位置上;
ax的系数必须为1.
概念应用 加深理解
1. 函数是指数函数,则.
2.已知指数函数的图象过点,则______.
跟进练习:
概念应用 加深理解
【规律方法】
2.求指数函数的解析式常用待定系数法.
例2. 在问题4中,如果平均每位游客出游一次可给当地带来1000元门票之外的收入,A地景区的门票价格为150元,比较这15年间A,B两地旅游收入变化情况.
利用图象中的数据得出:
当x=0时,f(0)-g(0)=412 000(万元)=41.2(亿元).
当x≈10.22时,f(10.22)≈g(10.22).
当x=14时,g(14)-f (14)≈34.73 (亿元).
当x<10.22时,f(x)>g(x).
当x>10.22时,f(x)
解:设经过x年,游客给A、B两地带来的收入
分别为f(x),g(x),则
概念应用 加深理解
g(x)=1000×278×1.11x .
这说明:
在2001年,游客给A地带来的收入比B地多41.2亿元;
随后的10年,游客给A地带来的收入仍高于B地,但g(x)比f(x)增长的速度快,大约2011年2月某个时刻就有f(x)=g(x),这时游客给A地带来的收入和B地差不多;
此后,游客给B地带来的收入高于A地了,由于g(x)增长的速度越来越快,而f(x)增长的速度不变,到2015年,游客给B地带来的收入已经高于了A地约34.73亿元了.
在实际问题中,经常会遇到如g(x)=1000×278×1.11x
指数增长模型:设原有量为N,每次的增长率为p,则经过x次增长,该量增长到y ,则y=N(1+p)x(x∈N).
指数衰减模型:设原有量为N,每次的衰减率为p,则经过x次减少,该量衰减到y ,则y =N (1-p) x(x ∈N).
形如 的函数,在,称为指数型函数. 这是刻画指数增长或指数衰减变化规律的非常有用的函数模型.
概念应用 加深理解
跟进练习:某地2012年底人口为500万,人均住房面积为6 m2,若该地区的人口年平均增长率为1%,要使2022年底该地区人均住房面积至少为7 m2,平均每年新增住房面积至少为多少万m2?
(精确到1万m2,参考数据:1.019≈1.093 7,1.0110≈1.104 6,1.0111≈1.115 7)
概念应用 加深理解
本节课你学到了那些知识?在探究规律和形成概念的过程中,用到了哪些数学思想方法?
课堂总结 提炼升华
函数概念
实际问题
数学抽象
数形结合思想
变化率是常数
从特殊到一般
数学运算
指数函数
一个概念:
一类函数:
核心素养:
数学思想:
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
