二次函数y=ax2的图象和性质课件
文档属性
| 名称 | 二次函数y=ax2的图象和性质课件 |  | |
| 格式 | zip | ||
| 文件大小 | 259.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-17 14:03:17 | ||
图片预览


文档简介
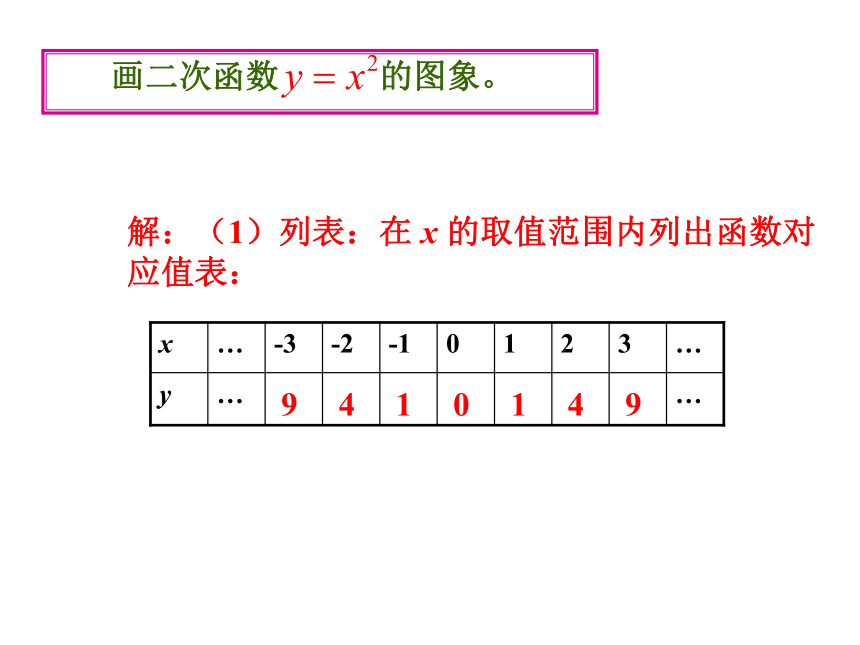
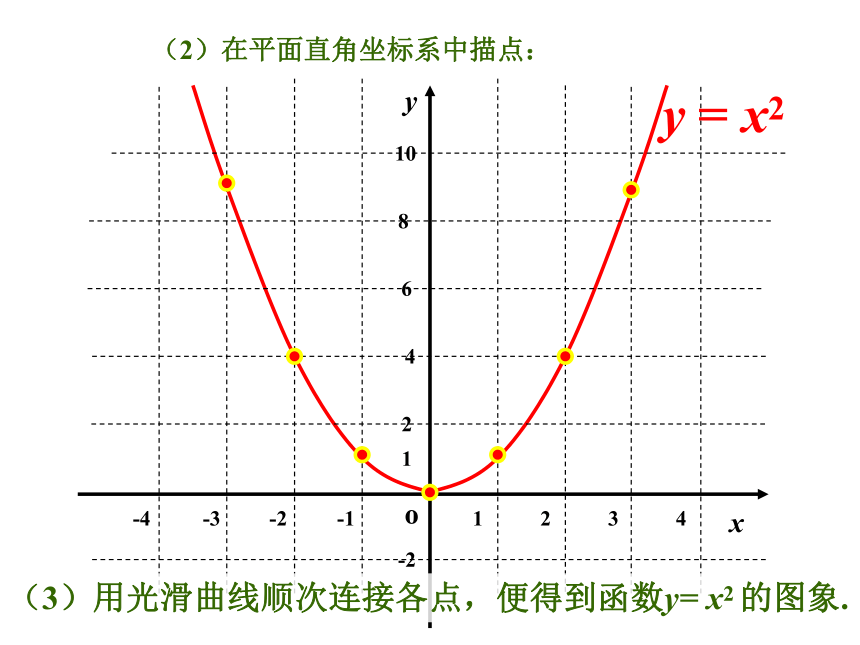
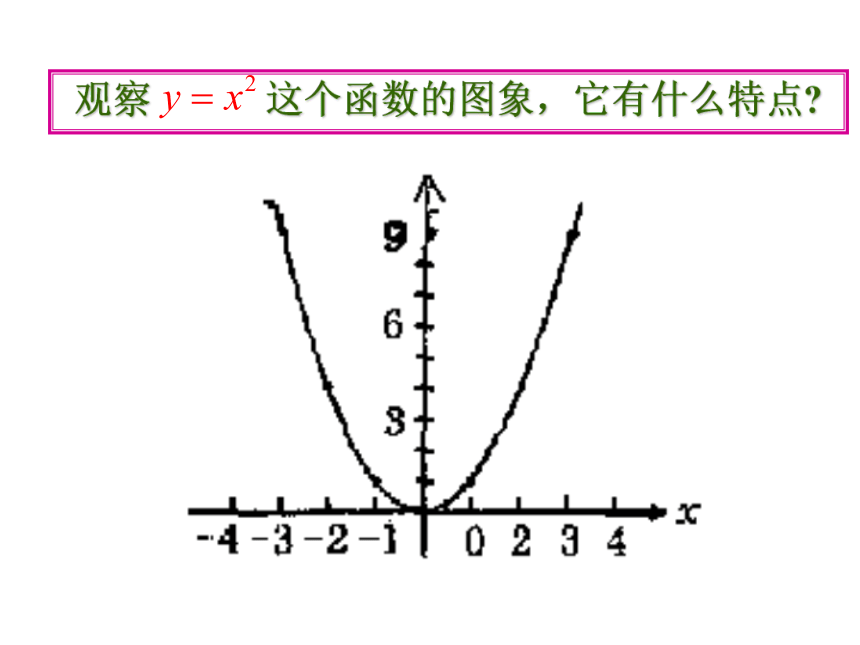
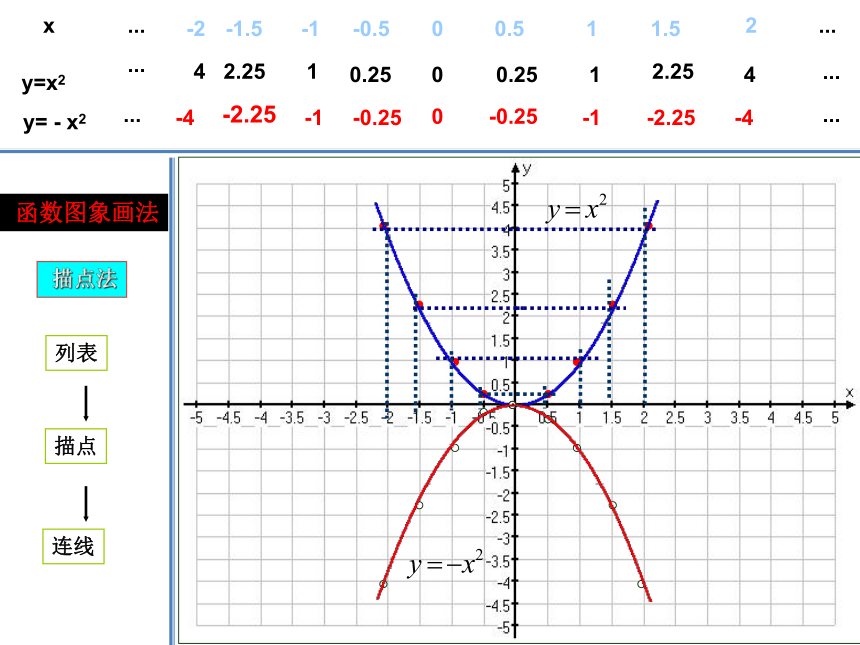
课件14张PPT。二次函数y=ax2的图象和性质请同学们回忆一下:研究一次函数的图象和性质的一般方法是什么?复习研究函数的一般方法数形结合结合图象讨论性质画函数图象1.列表2.描点3.连线 画二次函数 的图象。解:(1)列表:在 x 的取值范围内列出函数对应值表:……y…3210-1-2-3…x(2)在平面直角坐标系中描点: xyo-4-3-2-11234108642-21y = x2(3)用光滑曲线顺次连接各点,便得到函数y= x2 的图象.观察 这个函数的图象,它有什么特点?特点(1) 二次函数y=x2的图象是一条抛物线(2)抛物线 y=x2 的图象开口向上,对称轴是y轴,与对称轴的交点(0,0)是图象的顶点,也是最低点(3)在对称轴的左侧,抛物线从左到右下降;在对称轴右侧,抛物线从左到右上升 函数图象画法列表描点连线00.2512.2540.2512.254 描点法0-0.25-1-2.25-44-0.25-1-2.25-4 1.列表:2.描点:3.连线:只是开口
大小不同a>0,开口都向上;
对称轴都是y轴;
增减性相同顶点都是原点(0,0)00288222…………二次函数y=ax2的图象是什么形状?二次函数的图象是一条抛物线。a的绝对值越大开口越小试一试:1、函数y=2x2的图象的开口 ,对称轴是 ,顶点是 ;在对称轴的左
侧,y随x的增大而 ,在对称轴的右侧,
y随x的增大而 ; 2、函数y=-3x2的图象的开口 ,对称轴是 ,顶点是 ;在对称轴的左
侧,y随x的增大而 ,在对称轴的右侧,
y随x的增大而 ; 向上y轴(0,0)减小增大向下y轴(0,0)增大减小
3、观察函数y=x2的图象,则下列判断中正确的是 ( )
A 若a,b互为相反数,则x=a与x=b的函数值相等。
B 对于同一个自变量x,有两个函数值与它对应。
C 对任一个实数y,有两个x和它对应。
D 对任意实数x,都有y>0xyoA5、已知函数
是二次函数,且开口向上。
求m的值及二次函数的解析式,并回答y随x的变化规律2谢谢!
大小不同a>0,开口都向上;
对称轴都是y轴;
增减性相同顶点都是原点(0,0)00288222…………二次函数y=ax2的图象是什么形状?二次函数的图象是一条抛物线。a的绝对值越大开口越小试一试:1、函数y=2x2的图象的开口 ,对称轴是 ,顶点是 ;在对称轴的左
侧,y随x的增大而 ,在对称轴的右侧,
y随x的增大而 ; 2、函数y=-3x2的图象的开口 ,对称轴是 ,顶点是 ;在对称轴的左
侧,y随x的增大而 ,在对称轴的右侧,
y随x的增大而 ; 向上y轴(0,0)减小增大向下y轴(0,0)增大减小
3、观察函数y=x2的图象,则下列判断中正确的是 ( )
A 若a,b互为相反数,则x=a与x=b的函数值相等。
B 对于同一个自变量x,有两个函数值与它对应。
C 对任一个实数y,有两个x和它对应。
D 对任意实数x,都有y>0xyoA5、已知函数
是二次函数,且开口向上。
求m的值及二次函数的解析式,并回答y随x的变化规律2谢谢!
同课章节目录
