分式复习(一)
图片预览











文档简介
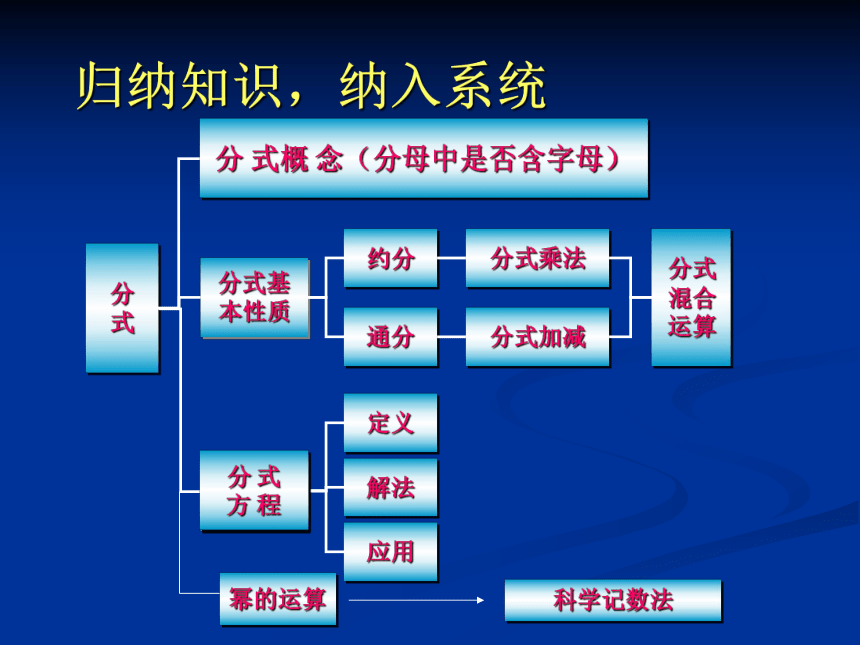
课件32张PPT。第十六章分式复习课归纳知识,纳入系统 分
式分 式概 念(分母中是否含字母)分式基
本性质约分通分定义解法应用分式乘法分式加减分式
混合
运算分 式
方 程分 式
方 程幂的运算科学记数法1.分式的定义:2.分式有意义的条件:B≠0分式无意义的条件:B = 03.分式值为 0 的条件:A=0且 B ≠0知识回顾一形如 ,其中 A ,B 都是整式, 且 B 中含有字母.2.下列各式中x满足什么条件时,分式有意义.3.下列分式一定有意义的是( )3B练习1.下列各式 是分式的有_____个.4.当x为何值时,下列分式的值为0?x=4x=1x=-3练习x>15.要使分式 的值为正数,则x的取值范围是_______.1.分式的基本性质:
分式的分子与分母同乘以(或除以)___________________,2.分式的符号法则:一个不为0的整式不变-A-B-BB-AB知识回顾二分式的值_________.1.写出下列等式中的未知的分子或分母.练习2.下列变形正确的是( )CA3.与分式 的值相等的分式是( )4.如果把分式 中的x和y的值都扩大3倍,B则分式的值( )A.扩大3倍 B.不变 C.缩小 D.缩小A.扩大3倍 B.不变 C.缩小 D.缩小把分子.分母的最大公因式(数)约去. 通分的关键是找最简公分母:各分母所有因式的最高次幂的积.1.约分:2.通分:知识回顾三把分母不相同的几个分式化成分母相同的分式.约分与通分的依据都是:分式的基本性质1、约分2、通分练习分式的运算
①加减:同分母相加减
异分母相加减 (先通分)
②乘法:
③除法:
④乘方:
知识回顾四⑤.分式的混合运算分式的混合运算:关键是要正确的使用相应的运算法则和运算顺序;正确的使用运算律,尽量简化运算过程;结果必须化为最简。
练习口答(1)(2)1.(3)(4); (1)(2)计算:专题四解分式方程去分母解整式方程验根3.解方程:无解1、(98西安)解方程:解:原方程可化为两边都乘以,并整理得;解得检验:x=1是原方程的根,x=2是增根∴原方程的根是x=1DA、2 B、-3
C、 0或-3 D、- 3或3DA、2 B、-3
C、 0或-3 D、- 3或3例2 已知 求A、B3、 已知 求A、B例5、已知 ,求 的值。剖析:通过已知,得出关系式 ,然后
利用 计算即可。专题五分式方程应用列分式方程解应用题的一般步骤1.审:分析题意,找出研究对象,建立等量关系.2.设:选择恰当的未知数,注意单位.3.列:根据等量关系正确列出方程.4.解:认真仔细.5.验:有三次检验.6.答:不要忘记写.一项工程,需要在规定日期内完成,如果甲队独做,恰好如期完成,如果乙队独做,就要超过规定3天,现在由甲、乙两队合作2天,剩下的由乙队独做,也刚好在规定日期内完成,
问规定日期是几天?解:设规定日期为x天,根据题意列方程请完成下面的过程2.已知轮船在静水中每小时行20千米,如果此船在某江中顺流航行72千米所用的时间与逆流航行48千米所用的时间相同,那么此江水每小时的流速是多少千米?
解:设江水每小时的流速是x千米,根据题意列方程请完成下面的过程4.某人骑自行车比步行每小时多走8千米,如果他步行12千米所用时间与骑车行36千米所用的时间相等,求他步行40千米用多少小时?
解:设他步行1千米用x小时,根据题意列方程请完成下面的过程(1)一件工作甲单独做要m小时完成,乙单独做要n小时完成,如果两人合做,完成这
件工作的时间是______ 小时; (2)某食堂有米m公斤,原计划每天用粮a公斤,现在每天节约用粮b公斤,则可以比原计划多用天数是______; 1.甲加工180个零件所用的时间,乙可以加工240个零件,已知甲每小时比乙少加工5个零件,求两人每小时各加工的零件个数.2.A,B两地相距135千米,有大,小两辆汽车从A地开往B地,大汽车比小汽车早出发5小时,小汽车比大汽车晚到30分钟.已知大、小汽车速度的比为2:5,求两辆汽车的速度. 甲:15
乙:20大:18千米/时
小:45千米/时 通过今天的复习,你有哪些新的收获?还有哪些疑问?小结:明天我们继续复习再见
式分 式概 念(分母中是否含字母)分式基
本性质约分通分定义解法应用分式乘法分式加减分式
混合
运算分 式
方 程分 式
方 程幂的运算科学记数法1.分式的定义:2.分式有意义的条件:B≠0分式无意义的条件:B = 03.分式值为 0 的条件:A=0且 B ≠0知识回顾一形如 ,其中 A ,B 都是整式, 且 B 中含有字母.2.下列各式中x满足什么条件时,分式有意义.3.下列分式一定有意义的是( )3B练习1.下列各式 是分式的有_____个.4.当x为何值时,下列分式的值为0?x=4x=1x=-3练习x>15.要使分式 的值为正数,则x的取值范围是_______.1.分式的基本性质:
分式的分子与分母同乘以(或除以)___________________,2.分式的符号法则:一个不为0的整式不变-A-B-BB-AB知识回顾二分式的值_________.1.写出下列等式中的未知的分子或分母.练习2.下列变形正确的是( )CA3.与分式 的值相等的分式是( )4.如果把分式 中的x和y的值都扩大3倍,B则分式的值( )A.扩大3倍 B.不变 C.缩小 D.缩小A.扩大3倍 B.不变 C.缩小 D.缩小把分子.分母的最大公因式(数)约去. 通分的关键是找最简公分母:各分母所有因式的最高次幂的积.1.约分:2.通分:知识回顾三把分母不相同的几个分式化成分母相同的分式.约分与通分的依据都是:分式的基本性质1、约分2、通分练习分式的运算
①加减:同分母相加减
异分母相加减 (先通分)
②乘法:
③除法:
④乘方:
知识回顾四⑤.分式的混合运算分式的混合运算:关键是要正确的使用相应的运算法则和运算顺序;正确的使用运算律,尽量简化运算过程;结果必须化为最简。
练习口答(1)(2)1.(3)(4); (1)(2)计算:专题四解分式方程去分母解整式方程验根3.解方程:无解1、(98西安)解方程:解:原方程可化为两边都乘以,并整理得;解得检验:x=1是原方程的根,x=2是增根∴原方程的根是x=1DA、2 B、-3
C、 0或-3 D、- 3或3DA、2 B、-3
C、 0或-3 D、- 3或3例2 已知 求A、B3、 已知 求A、B例5、已知 ,求 的值。剖析:通过已知,得出关系式 ,然后
利用 计算即可。专题五分式方程应用列分式方程解应用题的一般步骤1.审:分析题意,找出研究对象,建立等量关系.2.设:选择恰当的未知数,注意单位.3.列:根据等量关系正确列出方程.4.解:认真仔细.5.验:有三次检验.6.答:不要忘记写.一项工程,需要在规定日期内完成,如果甲队独做,恰好如期完成,如果乙队独做,就要超过规定3天,现在由甲、乙两队合作2天,剩下的由乙队独做,也刚好在规定日期内完成,
问规定日期是几天?解:设规定日期为x天,根据题意列方程请完成下面的过程2.已知轮船在静水中每小时行20千米,如果此船在某江中顺流航行72千米所用的时间与逆流航行48千米所用的时间相同,那么此江水每小时的流速是多少千米?
解:设江水每小时的流速是x千米,根据题意列方程请完成下面的过程4.某人骑自行车比步行每小时多走8千米,如果他步行12千米所用时间与骑车行36千米所用的时间相等,求他步行40千米用多少小时?
解:设他步行1千米用x小时,根据题意列方程请完成下面的过程(1)一件工作甲单独做要m小时完成,乙单独做要n小时完成,如果两人合做,完成这
件工作的时间是______ 小时; (2)某食堂有米m公斤,原计划每天用粮a公斤,现在每天节约用粮b公斤,则可以比原计划多用天数是______; 1.甲加工180个零件所用的时间,乙可以加工240个零件,已知甲每小时比乙少加工5个零件,求两人每小时各加工的零件个数.2.A,B两地相距135千米,有大,小两辆汽车从A地开往B地,大汽车比小汽车早出发5小时,小汽车比大汽车晚到30分钟.已知大、小汽车速度的比为2:5,求两辆汽车的速度. 甲:15
乙:20大:18千米/时
小:45千米/时 通过今天的复习,你有哪些新的收获?还有哪些疑问?小结:明天我们继续复习再见
