第二单元 圆柱和圆锥 单元复习卷 北京版六年级数学下册(含解析)
文档属性
| 名称 | 第二单元 圆柱和圆锥 单元复习卷 北京版六年级数学下册(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 242.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-20 15:19:06 | ||
图片预览




文档简介
第一单元 圆柱和圆锥 单元复习卷 北京版六年级数学下册
一、单选题
1.一个长方体、一个圆柱和一个圆锥底面积相等,高也相等。下面说法正确的是( )。
A.圆柱的体积比长方体的体积小一些
B.圆锥的体积是长方体体积的
C.圆柱的体积和圆锥的体积相等
D.圆锥的体积最大
2.下面四幅图中,不可能是圆柱侧面展开图的是( )。
A. B.
C. D.
3.一个玻璃密封器皿中有一些水,如图①,测得其高为20cm。如图②放置时,测得液面高10cm;如图③放置时,测得液面高16cm。容器中水的体积占容器容积的( )。
A. B. C. D.
4.如下图,要把下面三堆圆锥形沙子分别装在圆柱形的铁桶中(铁桶厚度忽略不计),下面是三名同学经过测量后得到的结论。
晶晶说:“第一堆和铁桶等底等高,能装下。”
明明说:“第二堆和铁桶等底,高是圆柱形铁桶的2倍,能装下。”
康康说:“第三堆和铁桶等高,底面半径是圆柱形铁桶的2倍,能装下”。
你认为( )的说法是正确的。
A.三人都对 B.晶晶和明明 C.明明和康康 D.晶晶和康康
5.典典、聪聪两人分别将一张长6.28cm,宽3.14cm的长方形纸以不同的方法围成一个圆柱(接头处不重叠),那么围成的两个圆柱的( )。
A.高一定相等 B.侧面积一定相等
C.底面积一定相等 D.体积一定相等
6.一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱的3倍,圆锥的体积是12dm3,圆柱的体积是( )dm3。
A.4 B.8 C.12 D.36
7.一个圆锥的体积是 12.56cm ,比与它等底等高的圆柱的体积少( )cm 。
A.12.56 B.25.12 C.3.14 D.6.28
8.营养学家建议,儿童每天水的摄入量约为1500 mL,要达到这个要求,明明每天用底面内直径为8 cm、高为10 cm的圆柱形水杯喝水,他每天喝( )杯水比较合适。
A.1 B.2 C.3 D.7
二、填空题
9.一个圆柱的侧面展开图是一个周长为 24 cm 的正方形,这个圆柱的侧面积是 cm2 。
10.一个圆锥形的沙堆,底面周长是 6.28 m,高是 1.5 m,这个沙堆的体积是 m3 。
11.自来水管的内直径是2cm,水管内水的流速是3厘米/秒,一位同学洗手忘记了关水龙头,2分钟后,另一个同学关上了,这期间共浪费 升水。
12.一台压路机前轮直径是 1.5m ,轮宽4m ,前轮滚动一周,压路的面积是 m 。
13.一个圆锥形容器里盛满水,水面高60厘米,将水倒入和它等底等高的圆柱形容器中,水的高度是 厘米。
三、计算题
14.计算下面图形的体积。
15.计算圆锥的体积。(单位:m)
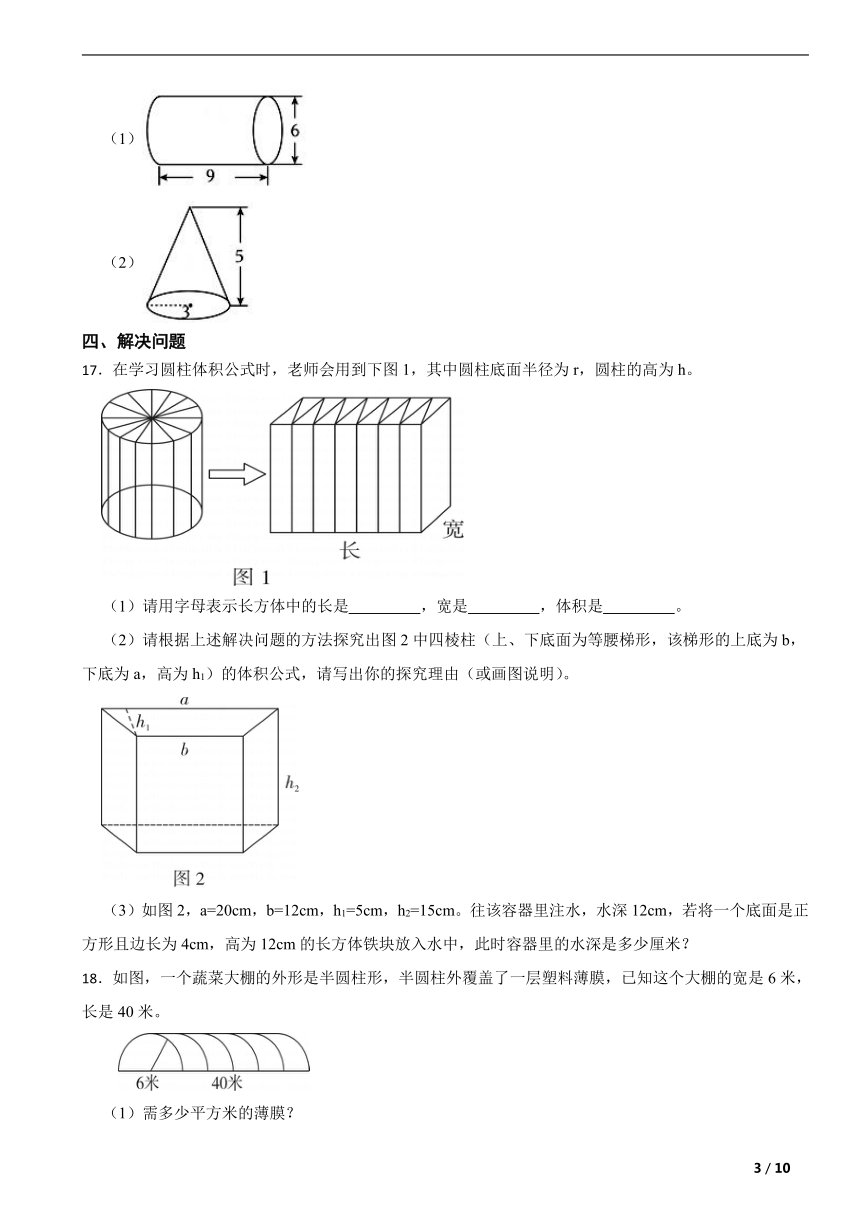
16.计算如图圆柱的表面积及圆锥的体积。(单位:厘米)
(1)
(2)
四、解决问题
17.在学习圆柱体积公式时,老师会用到下图1,其中圆柱底面半径为r,圆柱的高为h。
(1)请用字母表示长方体中的长是 ,宽是 ,体积是 。
(2)请根据上述解决问题的方法探究出图2中四棱柱(上、下底面为等腰梯形,该梯形的上底为b,下底为a,高为h1)的体积公式,请写出你的探究理由(或画图说明)。
(3)如图2,a=20cm,b=12cm,h1=5cm,h2=15cm。往该容器里注水,水深12cm,若将一个底面是正方形且边长为4cm,高为12cm的长方体铁块放入水中,此时容器里的水深是多少厘米?
18.如图,一个蔬菜大棚的外形是半圆柱形,半圆柱外覆盖了一层塑料薄膜,已知这个大棚的宽是6米,长是40米。
(1)需多少平方米的薄膜?
(2)整个大棚的空间是多少立方米?
19.把一张长62.8厘米、宽31.4厘米的长方形硬纸片卷成一个圆柱形纸筒(粘贴处宽度不计),这个纸筒的底面半径是多少厘米?
20.一个底面直径20厘米的圆柱形玻璃缸里有一个圆柱体物品,圆柱的浸没在水中,把这个圆柱体拿出来,缸内水面下降了2厘米,求这个圆柱体的体积是多少?
21.把一个圆柱形饼干盒外围商标纸展开,得到一个正方形.这个饼干盒的底面半径是5厘米,饼干盒的高是多少厘米?容积是多少立方厘米?
答案解析部分
1.【答案】B
【解析】【解答】解:选项A,一个长方体、一个圆柱和一个圆锥底面积相等,高也相等,圆柱的体积等于长方体的体积,原题说法错误;
选项B,一个长方体、一个圆柱和一个圆锥底面积相等,高也相等,圆锥的体积是圆柱体积的,也是长方体体积的,原题说法正确;
选项C,一个长方体、一个圆柱和一个圆锥底面积相等,高也相等,圆柱的体积是圆锥体积的3倍,原题说法错误;
选项D,一个长方体、一个圆柱和一个圆锥底面积相等,高也相等,圆锥的体积最小,原题说法错误。
故答案为:B。
【分析】圆柱的体积V=Sh,长方体的体积V=Sh,圆锥的体积V=Sh,一个长方体、一个圆柱和一个圆锥底面积相等,高也相等,圆柱和长方体的体积相等,圆柱的体积是圆锥体积的3倍。
2.【答案】D
【解析】【解答】解:梯形不可能是圆柱侧面展开图。
故答案为:D。
【分析】圆柱的侧面沿高剪开是长方形或正方形,沿斜线剪开得到的图形是一个平行四边形。
3.【答案】D
【解析】【解答】解:根据②可以把水的体积是10,
16-10=6,从②③可以看出空白部分的体积是6,
20-6=14,容器的体积是14,
10÷14=,容器中水的体积占容器容积的。
故答案为:D。
【分析】圆柱的底面积相等,体积和高可以理解为是一样的 。
4.【答案】B
【解析】【解答】解:晶晶:等底等高的圆柱体积是圆锥的3倍,所以第一堆和铁桶等底等高,能装下,说法正确;
明明:等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的3倍,如果底面积相等时,圆锥的高是圆柱高的3倍,所以第二堆和铁桶等底,高是圆柱形铁桶的2倍,能装下,说法正确;
康康:设圆柱的底面半径是r,则圆锥的底面半径是2r,高都是h,圆锥的体积×π(2r)2h=πr2h,圆柱的体积πr2h,πr2h>πr2h,说法错误。
故答案为:B。
【分析】等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的3倍,根据条件,分别分析每个人的话是否正确。
5.【答案】B
【解析】【解答】解:一张长方形纸,用不同的方法围成一个圆柱,接头处不重叠,围成的两个圆柱的侧面积一定相等。
故答案为:B。
【分析】用一个长方形围成圆柱,接头处不重叠,长方形的面积就是围成的圆柱侧面积。
6.【答案】C
【解析】【解答】解:12×3÷3=12(dm3)
故答案为:C。
【分析】等底等高的圆锥与圆柱,圆柱的体积是圆锥体积的3倍。等底的圆柱与圆锥,圆锥的高是圆柱的3倍,则圆柱与圆锥的体积相等。
7.【答案】B
【解析】【解答】解:12.56×(3-1)
=12.56×2
=25.12(立方厘米)
故答案为:B。
【分析】等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的3倍,所以圆锥的体积比与它等底等高的圆柱体积少的体积=圆锥的体积×(3-1)。
8.【答案】C
【解析】【解答】解:3.14×(8÷2)2×10
=50.24×10
=502.4(mL)
1500÷502.43(杯)
故答案为:C。
【分析】圆柱的体积=πr2h,每天喝水的总量÷一杯水的量=杯数。
9.【答案】36
【解析】【解答】解:24÷4=6(厘米)
6×6=36(平方厘米)
故答案为:36。
【分析】正方形的周长÷4=正方形的边长,正方形的边长×正方形的边长=正方形的面积,正方形的面积=这个圆柱的侧面积。
10.【答案】1.57
【解析】【解答】解:6.28÷3.14÷2=1(米)
3.14×1×1×1.5÷3=1.57(立方米)
故答案为:1.57。
【分析】底面周长÷π÷2=底面半径,π×底面半径的平方×高÷3=圆锥的体积。
11.【答案】1.1304
【解析】【解答】解:内半径:2÷2=1(厘米)
2分钟=120秒
3.14×1×1×3×120=9.42×120=1130.4(立方厘米)
1130.4立方厘米=1130.4毫升=1.1304升
故答案为:1.1304。
【分析】π×底面半径的平方×高=水流1秒钟的圆柱的体积;水流1秒钟的圆柱的体积×120秒=水流2分钟浪费的水的体积。
12.【答案】18.84
【解析】【解答】解:3.14×1.5×4
=3.14×6
=18.84(m2)
故答案为:18.84。
【分析】前轮滚动一周压路的面积就是前轮的侧面积,所以用底面周长乘轮宽即可求出压路的面积。
13.【答案】20
【解析】【解答】解:60÷3=20(厘米)
故答案为:20。
【分析】一个圆锥形容器里盛满水,将水倒入和它等底等高的圆柱形容器中,圆柱形容器里水的高度是圆锥形容器里水的高度的。
14.【答案】解 :图形看做圆柱的一半,
圆柱的底面直径是10厘米,底面半径是10÷2=5(厘米)
高是30+20=50(厘米)
3.14×5×5×50÷2
=78.5×50÷2
=3925÷2
=1962.5(cm3)
答:图形的体积是1962.5立方厘米。
【解析】【分析】底面直径÷2=底面半径,π×底面半径的平方=圆柱的底面积,圆柱的底面积×高=圆柱的体积,圆柱的体积÷2=图形的体积。
15.【答案】解:3.14×(8÷2)2×3×
=3.14×16×1
=50.24(m3)
【解析】【分析】已知圆锥的底面直径和高,要求圆锥的体积,将底面直径和高代入公式V=π(d÷2)2h即可。
16.【答案】(1)解:3.14×6×9+3.14×(6÷2)2×2
=18.84×9+3.14×9×2
=169.56+56.52
=226.08(平方厘米)
(2)解:×3.14×32×5
=×3.14×9×5
=47.1(立方厘米)
【解析】【分析】(1)圆柱的表面积=底面积×2+侧面积;圆柱的侧面积=底面周长×高;圆柱的底面积=π×底面半径×底面半径;
(2)圆锥的体积=底面积×高÷3;圆锥的底面积=π×底面半径×底面半径。
17.【答案】(1)πr;r;πr2h
(2)解:因为四棱柱的底是等腰梯形,过等腰梯形上底的两端作下底的垂线,沿着这两条垂线把四棱柱分成3份,把右边部分和左边部分合在一起可以得到一个长方体,长方体的体积=底面积×高,所以四棱柱的体积=底面积×高,即(a+b)×h1÷2×h2。
(3)解:4×4×12
=16×12
=192(平方厘米)
(20+12)×5÷2
=32×5÷2
=160÷2
=80(平方厘米)
192÷80=2.4(厘米)
12+2.4=14.4(厘米)
答:此时容器里的水深是14.4厘米。
【解析】【解答】解:(1)长方体中的长是πr,宽是r,体积是πr2h。
故答案为:(1)πr;r;πr2h。
【分析】(1)从图中可以看出,长方形的长=圆柱的底面周长÷2,长方形的宽=圆柱的底面半径,长方体的体积=圆柱的体积=πr2h;
(2)利用切割法把四棱柱进行切割,然后根据长方体的体积公式作答即可;
(3)铁块的体积=长×宽×高,容器的底面积=(上底+下底)×高÷2,所以放入长方体铁块后水面上升的高度=铁块的体积÷容器的底面积,故此时容器的水深=原来的水深+放入长方体铁块后水面上升的高度。
18.【答案】(1)解:3.14×6÷2×40
=9.42×40
=376.8(平方米)
答:需376.8平方米的薄膜。
(2)解:3.14×(6÷2)2×40÷2
=3.14×9×40÷2
=28.26×40÷2
=1130.4÷2
=565.2(立方米)
答:整个大棚的空间是565.2立方米。
【解析】【分析】(1)薄膜的面积=圆柱的侧面积÷2=大棚的宽×π×大棚的长÷2,据此代入数值作答即可;
(2)整个大棚的空间=圆柱的体积÷2,其中圆柱的体积=π×(底面直径÷2)2×大棚的长,据此代入数值作答即可。
19.【答案】解:62.8厘米、31.4厘米都可以作为纸筒的底面周长
62.8÷3.14÷2=10(厘米)
31.4÷3.14÷2=5(厘米)
答:这个纸筒的底面半径是10厘米或5厘米。
【解析】【分析】圆柱的底面周长÷π÷2=圆柱的底面半径。
20.【答案】解:20÷2=10(厘米)
3.14×10×10×2=628(立方厘米)
628÷=942(立方厘米)
答:这个圆柱体的体积是942立方厘米。
【解析】【分析】底面直径÷2=底面半径,π×底面半径的平方×水面下降的高度=圆柱的的体积,圆柱的的体积÷=圆柱的体积。
21.【答案】解:得到一个正方形,据此可知圆柱的底面周长和高相等
3.14×5×2=31.4(厘米)
3.14×5×5×31.4=2464.9(立方厘米)
答:饼干盒的高31.4厘米;容积是2464.9立方厘米。
【解析】【分析】π×底面半径×2=底面周长,底面周长=高,π×底面半径的平方×高=圆柱的体积。
1 / 1
一、单选题
1.一个长方体、一个圆柱和一个圆锥底面积相等,高也相等。下面说法正确的是( )。
A.圆柱的体积比长方体的体积小一些
B.圆锥的体积是长方体体积的
C.圆柱的体积和圆锥的体积相等
D.圆锥的体积最大
2.下面四幅图中,不可能是圆柱侧面展开图的是( )。
A. B.
C. D.
3.一个玻璃密封器皿中有一些水,如图①,测得其高为20cm。如图②放置时,测得液面高10cm;如图③放置时,测得液面高16cm。容器中水的体积占容器容积的( )。
A. B. C. D.
4.如下图,要把下面三堆圆锥形沙子分别装在圆柱形的铁桶中(铁桶厚度忽略不计),下面是三名同学经过测量后得到的结论。
晶晶说:“第一堆和铁桶等底等高,能装下。”
明明说:“第二堆和铁桶等底,高是圆柱形铁桶的2倍,能装下。”
康康说:“第三堆和铁桶等高,底面半径是圆柱形铁桶的2倍,能装下”。
你认为( )的说法是正确的。
A.三人都对 B.晶晶和明明 C.明明和康康 D.晶晶和康康
5.典典、聪聪两人分别将一张长6.28cm,宽3.14cm的长方形纸以不同的方法围成一个圆柱(接头处不重叠),那么围成的两个圆柱的( )。
A.高一定相等 B.侧面积一定相等
C.底面积一定相等 D.体积一定相等
6.一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱的3倍,圆锥的体积是12dm3,圆柱的体积是( )dm3。
A.4 B.8 C.12 D.36
7.一个圆锥的体积是 12.56cm ,比与它等底等高的圆柱的体积少( )cm 。
A.12.56 B.25.12 C.3.14 D.6.28
8.营养学家建议,儿童每天水的摄入量约为1500 mL,要达到这个要求,明明每天用底面内直径为8 cm、高为10 cm的圆柱形水杯喝水,他每天喝( )杯水比较合适。
A.1 B.2 C.3 D.7
二、填空题
9.一个圆柱的侧面展开图是一个周长为 24 cm 的正方形,这个圆柱的侧面积是 cm2 。
10.一个圆锥形的沙堆,底面周长是 6.28 m,高是 1.5 m,这个沙堆的体积是 m3 。
11.自来水管的内直径是2cm,水管内水的流速是3厘米/秒,一位同学洗手忘记了关水龙头,2分钟后,另一个同学关上了,这期间共浪费 升水。
12.一台压路机前轮直径是 1.5m ,轮宽4m ,前轮滚动一周,压路的面积是 m 。
13.一个圆锥形容器里盛满水,水面高60厘米,将水倒入和它等底等高的圆柱形容器中,水的高度是 厘米。
三、计算题
14.计算下面图形的体积。
15.计算圆锥的体积。(单位:m)
16.计算如图圆柱的表面积及圆锥的体积。(单位:厘米)
(1)
(2)
四、解决问题
17.在学习圆柱体积公式时,老师会用到下图1,其中圆柱底面半径为r,圆柱的高为h。
(1)请用字母表示长方体中的长是 ,宽是 ,体积是 。
(2)请根据上述解决问题的方法探究出图2中四棱柱(上、下底面为等腰梯形,该梯形的上底为b,下底为a,高为h1)的体积公式,请写出你的探究理由(或画图说明)。
(3)如图2,a=20cm,b=12cm,h1=5cm,h2=15cm。往该容器里注水,水深12cm,若将一个底面是正方形且边长为4cm,高为12cm的长方体铁块放入水中,此时容器里的水深是多少厘米?
18.如图,一个蔬菜大棚的外形是半圆柱形,半圆柱外覆盖了一层塑料薄膜,已知这个大棚的宽是6米,长是40米。
(1)需多少平方米的薄膜?
(2)整个大棚的空间是多少立方米?
19.把一张长62.8厘米、宽31.4厘米的长方形硬纸片卷成一个圆柱形纸筒(粘贴处宽度不计),这个纸筒的底面半径是多少厘米?
20.一个底面直径20厘米的圆柱形玻璃缸里有一个圆柱体物品,圆柱的浸没在水中,把这个圆柱体拿出来,缸内水面下降了2厘米,求这个圆柱体的体积是多少?
21.把一个圆柱形饼干盒外围商标纸展开,得到一个正方形.这个饼干盒的底面半径是5厘米,饼干盒的高是多少厘米?容积是多少立方厘米?
答案解析部分
1.【答案】B
【解析】【解答】解:选项A,一个长方体、一个圆柱和一个圆锥底面积相等,高也相等,圆柱的体积等于长方体的体积,原题说法错误;
选项B,一个长方体、一个圆柱和一个圆锥底面积相等,高也相等,圆锥的体积是圆柱体积的,也是长方体体积的,原题说法正确;
选项C,一个长方体、一个圆柱和一个圆锥底面积相等,高也相等,圆柱的体积是圆锥体积的3倍,原题说法错误;
选项D,一个长方体、一个圆柱和一个圆锥底面积相等,高也相等,圆锥的体积最小,原题说法错误。
故答案为:B。
【分析】圆柱的体积V=Sh,长方体的体积V=Sh,圆锥的体积V=Sh,一个长方体、一个圆柱和一个圆锥底面积相等,高也相等,圆柱和长方体的体积相等,圆柱的体积是圆锥体积的3倍。
2.【答案】D
【解析】【解答】解:梯形不可能是圆柱侧面展开图。
故答案为:D。
【分析】圆柱的侧面沿高剪开是长方形或正方形,沿斜线剪开得到的图形是一个平行四边形。
3.【答案】D
【解析】【解答】解:根据②可以把水的体积是10,
16-10=6,从②③可以看出空白部分的体积是6,
20-6=14,容器的体积是14,
10÷14=,容器中水的体积占容器容积的。
故答案为:D。
【分析】圆柱的底面积相等,体积和高可以理解为是一样的 。
4.【答案】B
【解析】【解答】解:晶晶:等底等高的圆柱体积是圆锥的3倍,所以第一堆和铁桶等底等高,能装下,说法正确;
明明:等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的3倍,如果底面积相等时,圆锥的高是圆柱高的3倍,所以第二堆和铁桶等底,高是圆柱形铁桶的2倍,能装下,说法正确;
康康:设圆柱的底面半径是r,则圆锥的底面半径是2r,高都是h,圆锥的体积×π(2r)2h=πr2h,圆柱的体积πr2h,πr2h>πr2h,说法错误。
故答案为:B。
【分析】等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的3倍,根据条件,分别分析每个人的话是否正确。
5.【答案】B
【解析】【解答】解:一张长方形纸,用不同的方法围成一个圆柱,接头处不重叠,围成的两个圆柱的侧面积一定相等。
故答案为:B。
【分析】用一个长方形围成圆柱,接头处不重叠,长方形的面积就是围成的圆柱侧面积。
6.【答案】C
【解析】【解答】解:12×3÷3=12(dm3)
故答案为:C。
【分析】等底等高的圆锥与圆柱,圆柱的体积是圆锥体积的3倍。等底的圆柱与圆锥,圆锥的高是圆柱的3倍,则圆柱与圆锥的体积相等。
7.【答案】B
【解析】【解答】解:12.56×(3-1)
=12.56×2
=25.12(立方厘米)
故答案为:B。
【分析】等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的3倍,所以圆锥的体积比与它等底等高的圆柱体积少的体积=圆锥的体积×(3-1)。
8.【答案】C
【解析】【解答】解:3.14×(8÷2)2×10
=50.24×10
=502.4(mL)
1500÷502.43(杯)
故答案为:C。
【分析】圆柱的体积=πr2h,每天喝水的总量÷一杯水的量=杯数。
9.【答案】36
【解析】【解答】解:24÷4=6(厘米)
6×6=36(平方厘米)
故答案为:36。
【分析】正方形的周长÷4=正方形的边长,正方形的边长×正方形的边长=正方形的面积,正方形的面积=这个圆柱的侧面积。
10.【答案】1.57
【解析】【解答】解:6.28÷3.14÷2=1(米)
3.14×1×1×1.5÷3=1.57(立方米)
故答案为:1.57。
【分析】底面周长÷π÷2=底面半径,π×底面半径的平方×高÷3=圆锥的体积。
11.【答案】1.1304
【解析】【解答】解:内半径:2÷2=1(厘米)
2分钟=120秒
3.14×1×1×3×120=9.42×120=1130.4(立方厘米)
1130.4立方厘米=1130.4毫升=1.1304升
故答案为:1.1304。
【分析】π×底面半径的平方×高=水流1秒钟的圆柱的体积;水流1秒钟的圆柱的体积×120秒=水流2分钟浪费的水的体积。
12.【答案】18.84
【解析】【解答】解:3.14×1.5×4
=3.14×6
=18.84(m2)
故答案为:18.84。
【分析】前轮滚动一周压路的面积就是前轮的侧面积,所以用底面周长乘轮宽即可求出压路的面积。
13.【答案】20
【解析】【解答】解:60÷3=20(厘米)
故答案为:20。
【分析】一个圆锥形容器里盛满水,将水倒入和它等底等高的圆柱形容器中,圆柱形容器里水的高度是圆锥形容器里水的高度的。
14.【答案】解 :图形看做圆柱的一半,
圆柱的底面直径是10厘米,底面半径是10÷2=5(厘米)
高是30+20=50(厘米)
3.14×5×5×50÷2
=78.5×50÷2
=3925÷2
=1962.5(cm3)
答:图形的体积是1962.5立方厘米。
【解析】【分析】底面直径÷2=底面半径,π×底面半径的平方=圆柱的底面积,圆柱的底面积×高=圆柱的体积,圆柱的体积÷2=图形的体积。
15.【答案】解:3.14×(8÷2)2×3×
=3.14×16×1
=50.24(m3)
【解析】【分析】已知圆锥的底面直径和高,要求圆锥的体积,将底面直径和高代入公式V=π(d÷2)2h即可。
16.【答案】(1)解:3.14×6×9+3.14×(6÷2)2×2
=18.84×9+3.14×9×2
=169.56+56.52
=226.08(平方厘米)
(2)解:×3.14×32×5
=×3.14×9×5
=47.1(立方厘米)
【解析】【分析】(1)圆柱的表面积=底面积×2+侧面积;圆柱的侧面积=底面周长×高;圆柱的底面积=π×底面半径×底面半径;
(2)圆锥的体积=底面积×高÷3;圆锥的底面积=π×底面半径×底面半径。
17.【答案】(1)πr;r;πr2h
(2)解:因为四棱柱的底是等腰梯形,过等腰梯形上底的两端作下底的垂线,沿着这两条垂线把四棱柱分成3份,把右边部分和左边部分合在一起可以得到一个长方体,长方体的体积=底面积×高,所以四棱柱的体积=底面积×高,即(a+b)×h1÷2×h2。
(3)解:4×4×12
=16×12
=192(平方厘米)
(20+12)×5÷2
=32×5÷2
=160÷2
=80(平方厘米)
192÷80=2.4(厘米)
12+2.4=14.4(厘米)
答:此时容器里的水深是14.4厘米。
【解析】【解答】解:(1)长方体中的长是πr,宽是r,体积是πr2h。
故答案为:(1)πr;r;πr2h。
【分析】(1)从图中可以看出,长方形的长=圆柱的底面周长÷2,长方形的宽=圆柱的底面半径,长方体的体积=圆柱的体积=πr2h;
(2)利用切割法把四棱柱进行切割,然后根据长方体的体积公式作答即可;
(3)铁块的体积=长×宽×高,容器的底面积=(上底+下底)×高÷2,所以放入长方体铁块后水面上升的高度=铁块的体积÷容器的底面积,故此时容器的水深=原来的水深+放入长方体铁块后水面上升的高度。
18.【答案】(1)解:3.14×6÷2×40
=9.42×40
=376.8(平方米)
答:需376.8平方米的薄膜。
(2)解:3.14×(6÷2)2×40÷2
=3.14×9×40÷2
=28.26×40÷2
=1130.4÷2
=565.2(立方米)
答:整个大棚的空间是565.2立方米。
【解析】【分析】(1)薄膜的面积=圆柱的侧面积÷2=大棚的宽×π×大棚的长÷2,据此代入数值作答即可;
(2)整个大棚的空间=圆柱的体积÷2,其中圆柱的体积=π×(底面直径÷2)2×大棚的长,据此代入数值作答即可。
19.【答案】解:62.8厘米、31.4厘米都可以作为纸筒的底面周长
62.8÷3.14÷2=10(厘米)
31.4÷3.14÷2=5(厘米)
答:这个纸筒的底面半径是10厘米或5厘米。
【解析】【分析】圆柱的底面周长÷π÷2=圆柱的底面半径。
20.【答案】解:20÷2=10(厘米)
3.14×10×10×2=628(立方厘米)
628÷=942(立方厘米)
答:这个圆柱体的体积是942立方厘米。
【解析】【分析】底面直径÷2=底面半径,π×底面半径的平方×水面下降的高度=圆柱的的体积,圆柱的的体积÷=圆柱的体积。
21.【答案】解:得到一个正方形,据此可知圆柱的底面周长和高相等
3.14×5×2=31.4(厘米)
3.14×5×5×31.4=2464.9(立方厘米)
答:饼干盒的高31.4厘米;容积是2464.9立方厘米。
【解析】【分析】π×底面半径×2=底面周长,底面周长=高,π×底面半径的平方×高=圆柱的体积。
1 / 1
