江西省新余市第四中学2024届九年级下学期开学考试数学试卷(含解析)
文档属性
| 名称 | 江西省新余市第四中学2024届九年级下学期开学考试数学试卷(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-20 00:00:00 | ||
图片预览




文档简介
新余市第四中学2024届九年级下学期开学考试数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.古典园林中的花窗通常利用对称构图,体现对称美.下面四个花窗图案,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.若关于x的一元二次方程有一个根是0,则k的值是( )
A. B.2 C.0 D.或2
3.“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).小亮随机地向大正方形内部区域投飞镖.若直角三角形两条直角边的长分别是2和1,则飞镖投到小正方形(阴影)区域的概率是( )
A. B. C. D.
4.我国古代数学家杨辉的《田亩比数乘除减法》中记载:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步?”翻译成数学问题是:一块矩形田地的面积为864平方步,它的宽比长少12步.如果设宽为x步,则可列出方程( )
A. B. C. D.
5.如图,在中,,,则的度数是( )
A. B. C. D.
6.如图,抛物线的对称轴为,抛物线与轴的一个交点在和之间,其部分图象如图所示.有下列结论:
①;
②;
③;
④若,,是该抛物线上的三点,则;
⑤(t为实数).其中正确结论的序号有( )
A.①②③④ B.①②④⑤ C.①②③⑤ D.①②④
二、填空题
7.点关于原点对称的点的坐标是__________.
8.设,是一元二次方程的两根,则_______.
9.将抛物线向左平移_______个单位后经过点.
10.如图,的对角线在y轴上,原点O为的中点,点D在第一象限内,轴,当双曲线经过点D时,则的面积为______.
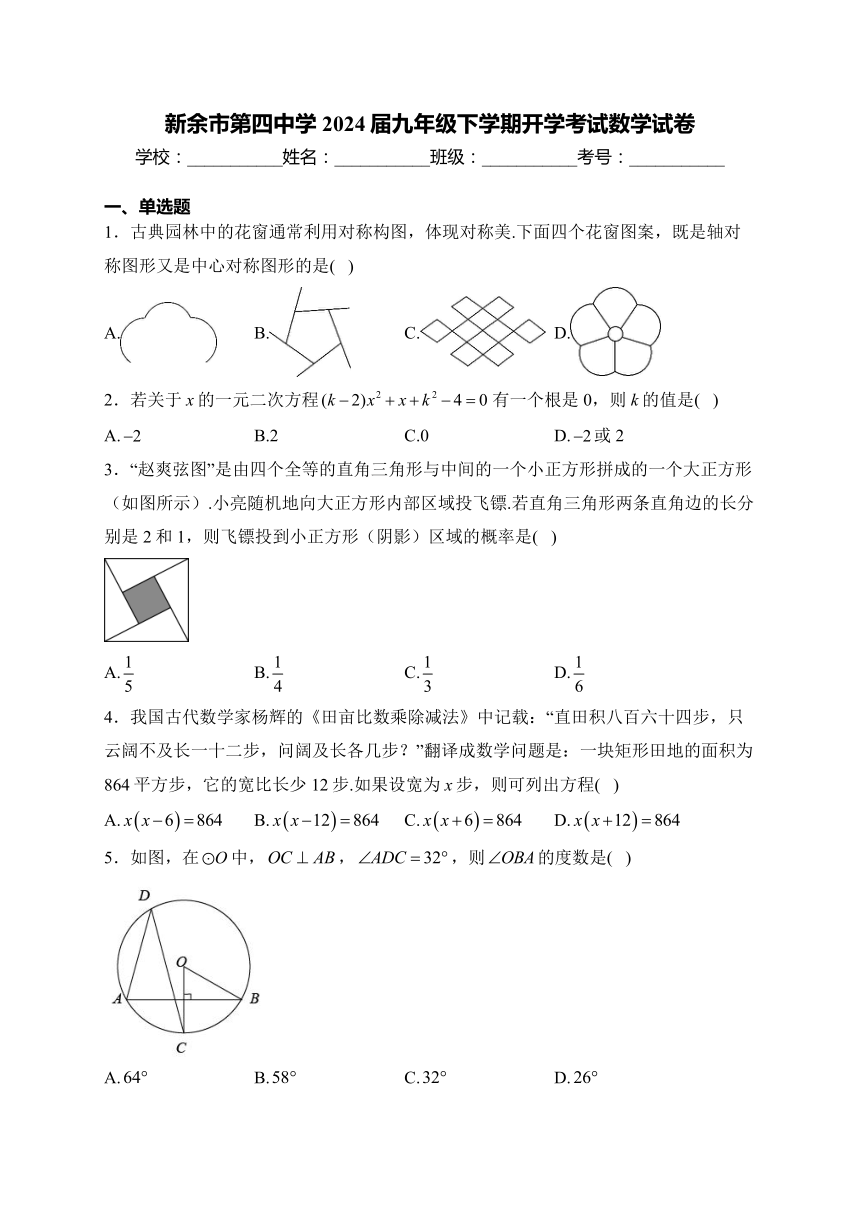
11.如图,将沿弦AB折叠,恰经过圆心O,若,则阴影部分的面积为_____.
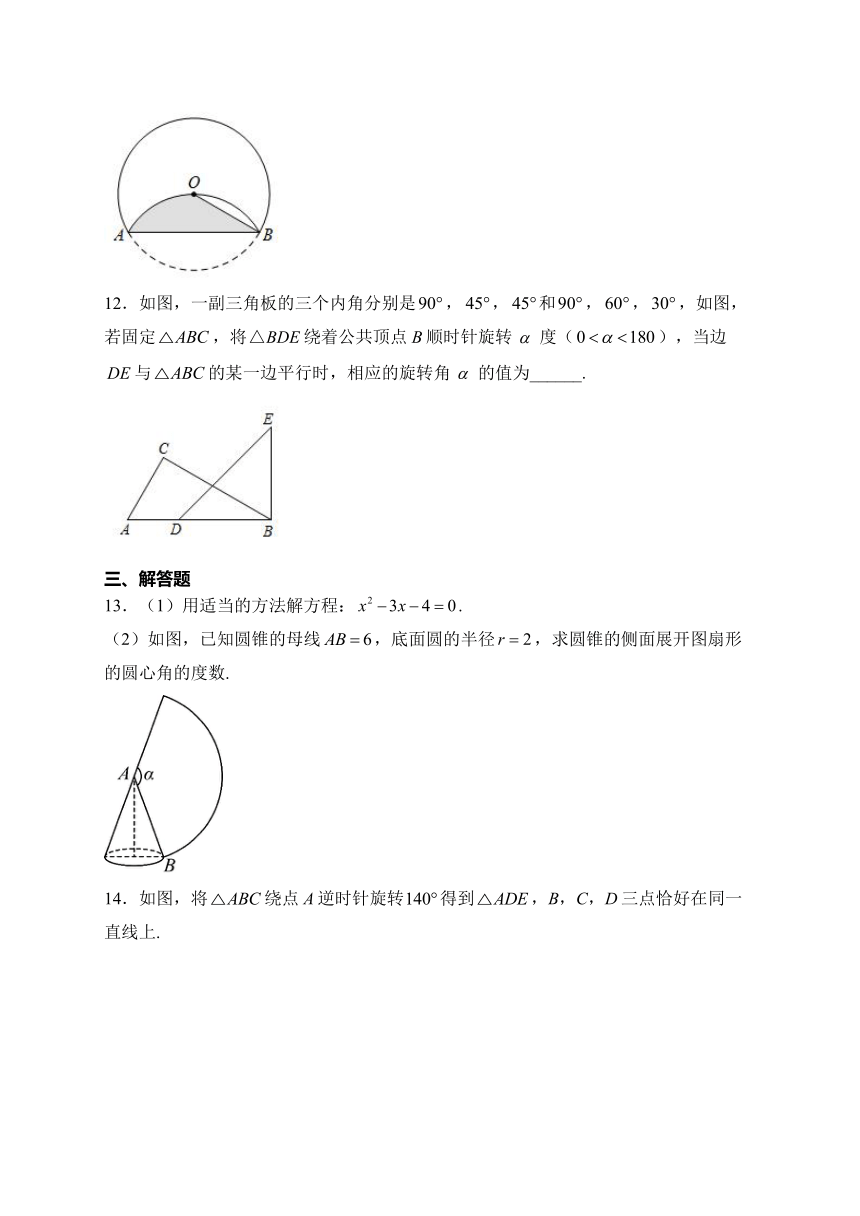
12.如图,一副三角板的三个内角分别是,,和,,,如图,若固定,将绕着公共顶点B顺时针旋转度(),当边与的某一边平行时,相应的旋转角的值为______.
三、解答题
13.(1)用适当的方法解方程:.
(2)如图,已知圆锥的母线,底面圆的半径,求圆锥的侧面展开图扇形的圆心角的度数.
14.如图,将绕点A逆时针旋转得到,B,C,D三点恰好在同一直线上.
(1)判断的形状;
(2)连接,若,求的度数.
15.按要求画图:①仅用无刻度的直尺;②保留必要的画图痕迹.
(1)如图1,画出的一个内接矩形;
(2)如图2,AB是的直径,CD是的弦,且,画出的一个内接正方形.
16.一个不透明的袋子里有4个小球,小球上各标有一个数字,分别是1,2,4,7.这些小球除标有的数字不同外其他都相同.
(1)从这个袋子里随机摸出一个小球,摸出标有数字“2”的小球的概率是________;
(2)先从袋中随机摸出一个小球,记下小球上的数字后,放回、摇匀,再从袋子中随机摸出一个小球,记下小球上的数字,第一次记下的数放在十位,第二次记下的数放在个位组成两位数,请运用画树状图或列表的方法,求这个两位数是偶数的概率.
17.已知关于x的方程.
(1)求证:无论k取任何实数值,方程总有实根;
(2)若等腰的一边,另两边b,c恰好是这个方程的两个根,求的周长.
18.如图,三个顶点的坐标分别为,,.
(1)作出向下平移4个单位长度后得到的;
(2)作出关于原点对称的,
(3)作出绕着点O逆时针旋转后的,并写出的坐标.
19.如图,直线与反比例函数的图象相交,两点,连接OA,OB.
(1)求k和n的值;
(2)求的面积.
20.“阳光玫瑰”葡萄近几年来广受各地消费者青睐,在云南省广泛种植.某水果经销商以每公斤15元的价格购进一批“阳光玫瑰”葡萄,若按每公斤30元的价格销售,平均每天可售出60公斤结合销售记录发现,若售价每降低1元,平均每天的销售量增加10公斤,为了尽快减少库存,该水果商决定降价销售.
(1)若一次降价2元,则每天的销售利润为_________元;
(2)销售单价定为每公斤多少元时,每天销售阳光玫瑰获得利润w最大?最大利润是多少元?
21.四边形ABCD是的内接四边形,AC为直径,,,垂足为E.
(1)求证:CD平分;
(2)判断直线ED与的位置关系,并说明理由;
(3)若,,求阴影部分的面积.
22.综合与实践
观察猜想:(1)如图1,与都是等腰直角三角形,其中,,,点E在线段上,连接,,则和的数量关系是______.
探索证明:(2)如图2,将(1)中的绕点C顺时针旋转,点E落在线段上,其他条件不变,此时的度数是______,探究线段,,之间的数量关系,并说明理由.
拓展探究:(3)如图3,是等腰直角三角形,其中,,D为外一点,且,连接,若,,请直接写出的长.
23.如图,已知抛物线与x轴交于、两点,与y轴交于C点.
(1)求该抛物线的函数表达式.
(2)如图1,当点P的坐标为时,求的面积.
(3)如图2,在抛物线的对称轴上是否存在点F,使是直角三角形?若存在,请求出点F的坐标;若不存在,请说明理由.
参考答案
1.答案:C
解析:A、是轴对称图形,不是中心对称图形,故此选项不符合题意;
B、既不是轴对称图形,也不是中心对称图形,故此选项不合题意;
C、既是轴对称图形,也是中心对称图形,故此选项符合题意;
D、是轴对称图形,不是中心对称图形,故此选项不合题意;
故选:C.
2.答案:A
解析:把代入一元二次方程,得
,
解得,,
而,即.
所以k的值为.
故选A.
3.答案:A
解析:根据题意分析可得:正方形ABCD边长为,故面积为5;
阴影部分边长为,面积为1;
则针扎到小正方形(阴影)区域的概率是即两部分面积的比值为.
故选:A.
4.答案:D
解析:设宽为x步,则长为步,
由题意得,,
故选:D.
5.答案:D
解析:在中,,
,
根据垂径定理可知,
根据圆周角定理可知,,
.
故选D.
6.答案:C
解析:①抛物线的对称轴为,
,
,故结论①正确;
②抛物线的开口向下,与x轴的一个交点在和之间,
抛物线与x轴的另一个交点在和之间,
抛物线与y轴的交点在负半轴上,
,故结论②正确;
③对于,当时,,
抛物线与x轴的另一个交点在和之间,开口向下,
点在第二象限,
,
由①,
,
,即:,故结论③正确;
④抛物线的开口向下,且对称轴为直线,
观察函数的图象可知:在抛物线上离对称轴水平距离越小,函数的值就越大,
,故结论④不正确.
⑤对于,当时,,当(t为实数)时,,
抛物线的对称轴为,
点为抛物线的顶点,
又抛物线的开口向下,
为抛物线的最大值,
,即:,故结论⑤正确;
综上所述:正确的结论是①②③⑤.
故选:C.
7.答案:
解析:根据中心对称的性质,得点关于原点对称点的坐标是.
故答案是:.
8.答案:0
解析:、是方程的两根,
,,
.
故答案为0.
9.答案:3
解析:将抛物线向左平移后经过点,
设平移后解析式为:,
则,
解得:或(不合题意舍去),
故将抛物线向左平移3个单位后经过点.
故答案为3.
10.答案:8
解析:连接BD,
四边形ABCD是平行四边形,且O点是AC的中点,
O点是BD的中点,
D点在反比例函数的图像上,且轴,
,
,
即的面积为8.
故答案为:8.
11.答案:
解析:过点O作于点D,交劣弧AB于点E,如图所示:
由题意可得:,,
,
,,,
弓形AB的面积为,
阴影部分的面积为;
故答案为.
12.答案:45°,75°,165°
解析:①如图1中,当时,
,可得旋转角;
②如图2中,当时,
,可得旋转角;
③如图3中,当时,作,
则,
,,
,可得旋转角,
综上所述,满足条件的旋转角为45°,75°,165°,
故答案为:45°,75°,165°.
13.答案:(1),
(2)
解析:(1),
,
或,
解得,;
(2)设扇形圆心角度数为,
由题意得,,
解得,
这个圆锥的侧面展开图扇形的圆心角的度数为.
14.答案:(1)顶角为的等腰三角形
(2)
解析:(1)绕点A逆时针旋转得到,
,,
是以顶角为的等腰三角形;
(2)绕点A逆时针旋转得到,
,,,
在中,,
在中,,
,
,
,
在中,,
的度数为.
15.答案:(1)见解析
(2)见解析
解析:(1)如图所示,过O作的直径AC与BD,连接AB,BC,CD,DA,则四边形ABCD即为所求;
(2)如图所示,延长AC,BD交于点E,连接AD,BC交于点F,连接EF并延长交于G,H,连接AH,HB,BG,GA,则四边形AHBG即为所求.
16.答案:(1)
(2)
解析:(1)由题意可得,
从袋中机摸出一个小球,则摸出标有数字“2”的小球的概率是.
(2)画树状图如下
由树状图可知一共有16种可能,且每种结果出现的可能性相同,其中这个两位数是偶数的结果数有8种,
这个两位数是偶数的概率为.
17.答案:(1)见解析
(2)7或8
解析:(1)证明:关于x的方程,
,
无论k取任何实数值,,即,
无论k取任何实数值,方程总有实根;
(2)等腰的一边,两边b,c恰好是这个方程的两个根,
当时,,即,
,
此时方程为:,
,
,
的周长;
当或时,
把代入方程得:
解得:,此时的方程为,
解得:,,
的三边长为3,3,2,
的周长;
综上所述,的周长为7或8.
18.答案:(1)图见解析
(2)图见解析
(3)图见解析;
解析:(1)如图,即为所求;
(2)如图,即为所求;
(3)如图,即为所求,则.
19.答案:(1),
(2)
解析:(1)点在直线上,
,解得,
,
反比例函数的图象也经过点,
,解得;
(2)设直线分别与x轴,y轴相交于点C,点D,
当时,即,,,
当时,,,
点在直线上,
.即,
.
20.答案:(1)1040
(2)将商品的销售单价定为25.5元时,商场每天销售该商品获得的利润w最大,最大利润是1102.5元
解析:(1)根据题意,降价2元则销售量为(斤),
销售利润为:(元),
所以,若降价2元,则每天的销售利润是1040元;
故答案为:1040;
(2)设每公斤销售单价降价了x元,根据题意得:
,
,
当时,w有最大值,最大值为1102.5,
此时,
答:将商品的销售单价定为25.5元时,商场每天销售该商品获得的利润w最大,最大利润是1102.5元.
21.答案:(1)见解析
(2)相切;理由见解析
(3)
解析:(1)证明:,
,
,
,
即CD平分;
(2)直线ED与相切.
理由如下:连接OD,如图,
,
,
而,
,
,
,
,
为的切线;
(3)作于H,则四边形ODEH为矩形,
,
,,
,
,
在中,,
,
阴影部分的面积=
.
22.答案:(1)
(2),
(3)
解析:(1),,,
,
,
故答案为:;
(2),,理由如下:
,
,
又,,
,,
,;,
;
,
,
故答案为:;
(3)如图,过点C作,且,连接,,
,,,
,
又,,
,
,
,
.
23.答案:(1)
(2)6
(3)或或或
解析:(1)将点,代入,得
,
解得,
所以函数关系式为;
(2)当时,,
.
设直线的关系式为,
将代入,得
,
解得,
所以直线的关系式为.
过点P作交于点G,如图所示.
,
,
;
(3)存在点F,使使直角三角形,理由如下:
,
∴抛物线得对称轴为直线.
设,
,,.
当时,,
解得,
或;
当时,
,
解得,
;
当时,
,
解得,
.
综上所述,点F的坐标为或或或.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.古典园林中的花窗通常利用对称构图,体现对称美.下面四个花窗图案,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.若关于x的一元二次方程有一个根是0,则k的值是( )
A. B.2 C.0 D.或2
3.“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).小亮随机地向大正方形内部区域投飞镖.若直角三角形两条直角边的长分别是2和1,则飞镖投到小正方形(阴影)区域的概率是( )
A. B. C. D.
4.我国古代数学家杨辉的《田亩比数乘除减法》中记载:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步?”翻译成数学问题是:一块矩形田地的面积为864平方步,它的宽比长少12步.如果设宽为x步,则可列出方程( )
A. B. C. D.
5.如图,在中,,,则的度数是( )
A. B. C. D.
6.如图,抛物线的对称轴为,抛物线与轴的一个交点在和之间,其部分图象如图所示.有下列结论:
①;
②;
③;
④若,,是该抛物线上的三点,则;
⑤(t为实数).其中正确结论的序号有( )
A.①②③④ B.①②④⑤ C.①②③⑤ D.①②④
二、填空题
7.点关于原点对称的点的坐标是__________.
8.设,是一元二次方程的两根,则_______.
9.将抛物线向左平移_______个单位后经过点.
10.如图,的对角线在y轴上,原点O为的中点,点D在第一象限内,轴,当双曲线经过点D时,则的面积为______.
11.如图,将沿弦AB折叠,恰经过圆心O,若,则阴影部分的面积为_____.
12.如图,一副三角板的三个内角分别是,,和,,,如图,若固定,将绕着公共顶点B顺时针旋转度(),当边与的某一边平行时,相应的旋转角的值为______.
三、解答题
13.(1)用适当的方法解方程:.
(2)如图,已知圆锥的母线,底面圆的半径,求圆锥的侧面展开图扇形的圆心角的度数.
14.如图,将绕点A逆时针旋转得到,B,C,D三点恰好在同一直线上.
(1)判断的形状;
(2)连接,若,求的度数.
15.按要求画图:①仅用无刻度的直尺;②保留必要的画图痕迹.
(1)如图1,画出的一个内接矩形;
(2)如图2,AB是的直径,CD是的弦,且,画出的一个内接正方形.
16.一个不透明的袋子里有4个小球,小球上各标有一个数字,分别是1,2,4,7.这些小球除标有的数字不同外其他都相同.
(1)从这个袋子里随机摸出一个小球,摸出标有数字“2”的小球的概率是________;
(2)先从袋中随机摸出一个小球,记下小球上的数字后,放回、摇匀,再从袋子中随机摸出一个小球,记下小球上的数字,第一次记下的数放在十位,第二次记下的数放在个位组成两位数,请运用画树状图或列表的方法,求这个两位数是偶数的概率.
17.已知关于x的方程.
(1)求证:无论k取任何实数值,方程总有实根;
(2)若等腰的一边,另两边b,c恰好是这个方程的两个根,求的周长.
18.如图,三个顶点的坐标分别为,,.
(1)作出向下平移4个单位长度后得到的;
(2)作出关于原点对称的,
(3)作出绕着点O逆时针旋转后的,并写出的坐标.
19.如图,直线与反比例函数的图象相交,两点,连接OA,OB.
(1)求k和n的值;
(2)求的面积.
20.“阳光玫瑰”葡萄近几年来广受各地消费者青睐,在云南省广泛种植.某水果经销商以每公斤15元的价格购进一批“阳光玫瑰”葡萄,若按每公斤30元的价格销售,平均每天可售出60公斤结合销售记录发现,若售价每降低1元,平均每天的销售量增加10公斤,为了尽快减少库存,该水果商决定降价销售.
(1)若一次降价2元,则每天的销售利润为_________元;
(2)销售单价定为每公斤多少元时,每天销售阳光玫瑰获得利润w最大?最大利润是多少元?
21.四边形ABCD是的内接四边形,AC为直径,,,垂足为E.
(1)求证:CD平分;
(2)判断直线ED与的位置关系,并说明理由;
(3)若,,求阴影部分的面积.
22.综合与实践
观察猜想:(1)如图1,与都是等腰直角三角形,其中,,,点E在线段上,连接,,则和的数量关系是______.
探索证明:(2)如图2,将(1)中的绕点C顺时针旋转,点E落在线段上,其他条件不变,此时的度数是______,探究线段,,之间的数量关系,并说明理由.
拓展探究:(3)如图3,是等腰直角三角形,其中,,D为外一点,且,连接,若,,请直接写出的长.
23.如图,已知抛物线与x轴交于、两点,与y轴交于C点.
(1)求该抛物线的函数表达式.
(2)如图1,当点P的坐标为时,求的面积.
(3)如图2,在抛物线的对称轴上是否存在点F,使是直角三角形?若存在,请求出点F的坐标;若不存在,请说明理由.
参考答案
1.答案:C
解析:A、是轴对称图形,不是中心对称图形,故此选项不符合题意;
B、既不是轴对称图形,也不是中心对称图形,故此选项不合题意;
C、既是轴对称图形,也是中心对称图形,故此选项符合题意;
D、是轴对称图形,不是中心对称图形,故此选项不合题意;
故选:C.
2.答案:A
解析:把代入一元二次方程,得
,
解得,,
而,即.
所以k的值为.
故选A.
3.答案:A
解析:根据题意分析可得:正方形ABCD边长为,故面积为5;
阴影部分边长为,面积为1;
则针扎到小正方形(阴影)区域的概率是即两部分面积的比值为.
故选:A.
4.答案:D
解析:设宽为x步,则长为步,
由题意得,,
故选:D.
5.答案:D
解析:在中,,
,
根据垂径定理可知,
根据圆周角定理可知,,
.
故选D.
6.答案:C
解析:①抛物线的对称轴为,
,
,故结论①正确;
②抛物线的开口向下,与x轴的一个交点在和之间,
抛物线与x轴的另一个交点在和之间,
抛物线与y轴的交点在负半轴上,
,故结论②正确;
③对于,当时,,
抛物线与x轴的另一个交点在和之间,开口向下,
点在第二象限,
,
由①,
,
,即:,故结论③正确;
④抛物线的开口向下,且对称轴为直线,
观察函数的图象可知:在抛物线上离对称轴水平距离越小,函数的值就越大,
,故结论④不正确.
⑤对于,当时,,当(t为实数)时,,
抛物线的对称轴为,
点为抛物线的顶点,
又抛物线的开口向下,
为抛物线的最大值,
,即:,故结论⑤正确;
综上所述:正确的结论是①②③⑤.
故选:C.
7.答案:
解析:根据中心对称的性质,得点关于原点对称点的坐标是.
故答案是:.
8.答案:0
解析:、是方程的两根,
,,
.
故答案为0.
9.答案:3
解析:将抛物线向左平移后经过点,
设平移后解析式为:,
则,
解得:或(不合题意舍去),
故将抛物线向左平移3个单位后经过点.
故答案为3.
10.答案:8
解析:连接BD,
四边形ABCD是平行四边形,且O点是AC的中点,
O点是BD的中点,
D点在反比例函数的图像上,且轴,
,
,
即的面积为8.
故答案为:8.
11.答案:
解析:过点O作于点D,交劣弧AB于点E,如图所示:
由题意可得:,,
,
,,,
弓形AB的面积为,
阴影部分的面积为;
故答案为.
12.答案:45°,75°,165°
解析:①如图1中,当时,
,可得旋转角;
②如图2中,当时,
,可得旋转角;
③如图3中,当时,作,
则,
,,
,可得旋转角,
综上所述,满足条件的旋转角为45°,75°,165°,
故答案为:45°,75°,165°.
13.答案:(1),
(2)
解析:(1),
,
或,
解得,;
(2)设扇形圆心角度数为,
由题意得,,
解得,
这个圆锥的侧面展开图扇形的圆心角的度数为.
14.答案:(1)顶角为的等腰三角形
(2)
解析:(1)绕点A逆时针旋转得到,
,,
是以顶角为的等腰三角形;
(2)绕点A逆时针旋转得到,
,,,
在中,,
在中,,
,
,
,
在中,,
的度数为.
15.答案:(1)见解析
(2)见解析
解析:(1)如图所示,过O作的直径AC与BD,连接AB,BC,CD,DA,则四边形ABCD即为所求;
(2)如图所示,延长AC,BD交于点E,连接AD,BC交于点F,连接EF并延长交于G,H,连接AH,HB,BG,GA,则四边形AHBG即为所求.
16.答案:(1)
(2)
解析:(1)由题意可得,
从袋中机摸出一个小球,则摸出标有数字“2”的小球的概率是.
(2)画树状图如下
由树状图可知一共有16种可能,且每种结果出现的可能性相同,其中这个两位数是偶数的结果数有8种,
这个两位数是偶数的概率为.
17.答案:(1)见解析
(2)7或8
解析:(1)证明:关于x的方程,
,
无论k取任何实数值,,即,
无论k取任何实数值,方程总有实根;
(2)等腰的一边,两边b,c恰好是这个方程的两个根,
当时,,即,
,
此时方程为:,
,
,
的周长;
当或时,
把代入方程得:
解得:,此时的方程为,
解得:,,
的三边长为3,3,2,
的周长;
综上所述,的周长为7或8.
18.答案:(1)图见解析
(2)图见解析
(3)图见解析;
解析:(1)如图,即为所求;
(2)如图,即为所求;
(3)如图,即为所求,则.
19.答案:(1),
(2)
解析:(1)点在直线上,
,解得,
,
反比例函数的图象也经过点,
,解得;
(2)设直线分别与x轴,y轴相交于点C,点D,
当时,即,,,
当时,,,
点在直线上,
.即,
.
20.答案:(1)1040
(2)将商品的销售单价定为25.5元时,商场每天销售该商品获得的利润w最大,最大利润是1102.5元
解析:(1)根据题意,降价2元则销售量为(斤),
销售利润为:(元),
所以,若降价2元,则每天的销售利润是1040元;
故答案为:1040;
(2)设每公斤销售单价降价了x元,根据题意得:
,
,
当时,w有最大值,最大值为1102.5,
此时,
答:将商品的销售单价定为25.5元时,商场每天销售该商品获得的利润w最大,最大利润是1102.5元.
21.答案:(1)见解析
(2)相切;理由见解析
(3)
解析:(1)证明:,
,
,
,
即CD平分;
(2)直线ED与相切.
理由如下:连接OD,如图,
,
,
而,
,
,
,
,
为的切线;
(3)作于H,则四边形ODEH为矩形,
,
,,
,
,
在中,,
,
阴影部分的面积=
.
22.答案:(1)
(2),
(3)
解析:(1),,,
,
,
故答案为:;
(2),,理由如下:
,
,
又,,
,,
,;,
;
,
,
故答案为:;
(3)如图,过点C作,且,连接,,
,,,
,
又,,
,
,
,
.
23.答案:(1)
(2)6
(3)或或或
解析:(1)将点,代入,得
,
解得,
所以函数关系式为;
(2)当时,,
.
设直线的关系式为,
将代入,得
,
解得,
所以直线的关系式为.
过点P作交于点G,如图所示.
,
,
;
(3)存在点F,使使直角三角形,理由如下:
,
∴抛物线得对称轴为直线.
设,
,,.
当时,,
解得,
或;
当时,
,
解得,
;
当时,
,
解得,
.
综上所述,点F的坐标为或或或.
同课章节目录
