八年级数学菱形综合
图片预览









文档简介
课件45张PPT。
菱形衣帽架菱形丝袜商 标菱形建筑法兰西菱形队形一、探索并掌握菱形的性质和判别条件,以及菱形的对称性。
二、经历探索菱形的性质和判别条件的过程,在操作活动和观察分析过程中养成主动探究的习惯,形成初步的审美意识,进一步了解和体会 说理的基本方法。
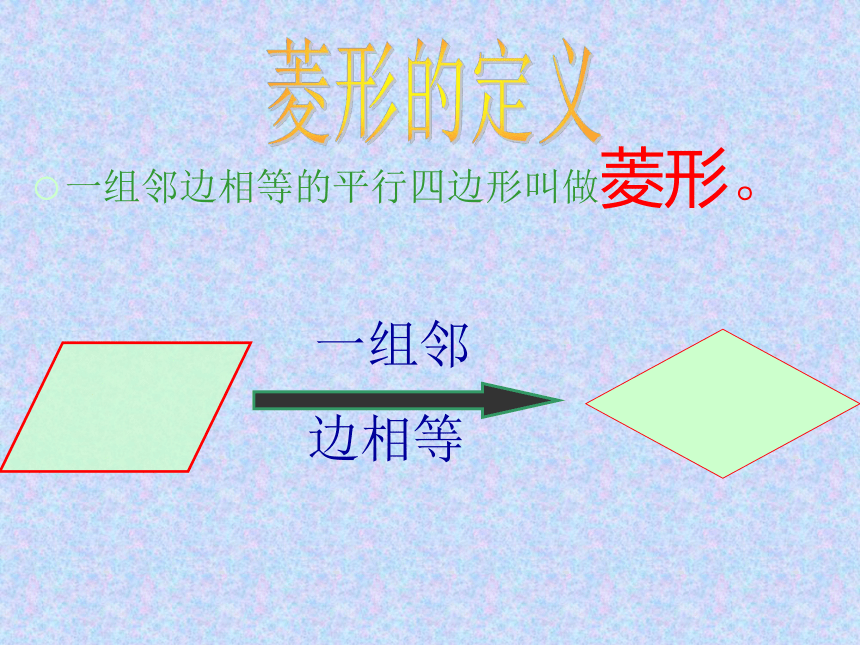
学习目标一组邻边相等的平行四边形叫做菱形。 一组邻
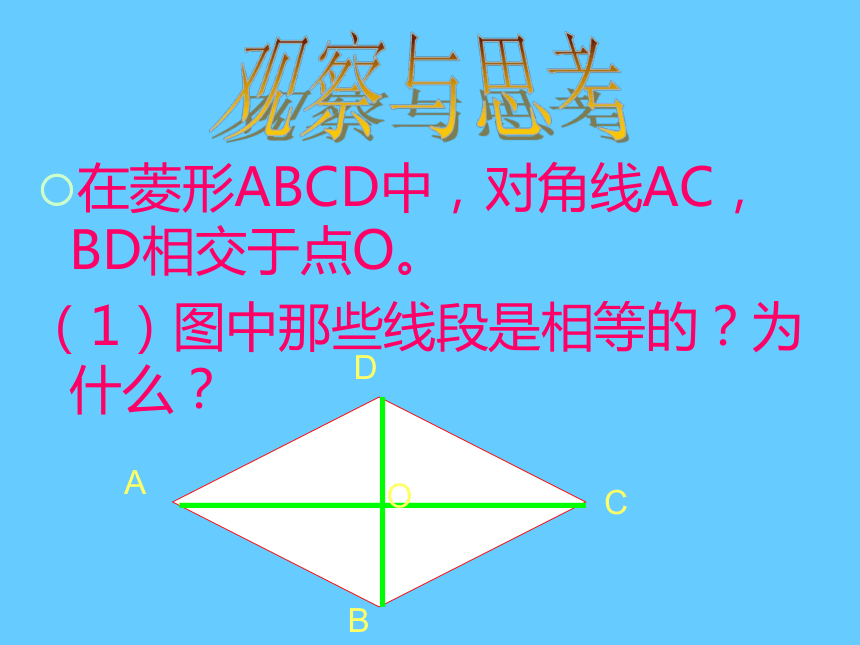
边相等菱形的定义在菱形ABCD中,对角线AC,BD相交于点O。
(1)图中那些线段是相等的?为什么?ABCDO观察与思考(2)图中那些角是相等的?为什么?ABCDO观察与思考(3)两条对角线有什么特定的位置关系,为什么?ABCDO观察与思考1、菱形是轴对称图形吗?如果是,那么它有几条对称轴?
观察与思考如何利用折纸、剪切的方法,既快又准确的剪出一个菱形的纸片?动手试一试1、两条等宽的纸条交叉重叠在一起,重叠的部分是菱形吗?为什么?动脑想一想有一组邻边相等的平行四边形叫做菱形;菱形的定义:一组邻边相等的平行四形是菱形。木工在做菱形的窗格时,总是保证四条边框一样长,你能说出其中的道理吗? 四条边都相等的平行四边形是菱形动脑想一想请观察刚才得到的菱形纸片上的折痕,再结合刚才的折纸操作,想一想其中的道理是什么?
对角线互相垂直的平行四边形是菱形。动脑想一想 他是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗? 如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?两组对边
分别平行情景创设我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,我们已经研究了一种特殊的平行四边形——矩形 ;这堂课还要研究另一种特殊的平行四边形——菱形菱形的性质:(1)菱形具有平行四边形的一切性质;(2)菱形的四条边都相等;(3)菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角;(4)菱形是轴对对称图形;也是中心对称图形;已知:菱形ABCD的对角线AC和BD相交于点O,如下图,证明:∵四边形ABCD是菱形在△ABD中,
又∵BO=DO∴AB=AD(菱形的四条边都相等)∴AC⊥BD,AC平分∠BAD同理: AC平分∠BCD;
BD平分∠ABC和∠ADC
求证:AC⊥BD ;
AC平分∠BAD和∠BCD ;BD平分∠ABC和∠ADC 命题:菱形的对角线互相垂直平分,
并且每一条对角线平分一组对角;相等的线段:相等的角:等腰三角形有:直角三角形有:全等三角形有:已知四边形ABCD是菱形AB=CD=AD=BC
OA=OC OB=OD∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8△ABC △ DBC △ACD △ABDRt△AOB Rt△BOC Rt△COD Rt△DOARt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACDABCDO12345678【菱形的面积公式】OES菱形=BC. AE思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积公式吗? 菱形的面积=底×高=对角线乘积的一半1、如图所示,平行四边形ABCD的两条对角线AC、BD相交于O。AB=√5,AO=2,OB=1
(1)AC与BD互相垂直吗?为什么?
(2)平行四边形ABCD是菱形吗?为什么?ABCDO典例与精练 ̄ ̄ ̄2、在菱形ABCD中,O是两条对角线交点。已知AB=5cm,AO=4cm,求对角线BD的长。ABCDO典例与精练合作与交流1、如图,菱形ABCD花坛的边长为20米,∠BAC=60.沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(分别精确到0.01米和0.01平方米)CABD解:∵花坛ABCD是菱形,∴AC⊥BD, ∠BAO=30. ∴BO=0.5*AB=0.5*20=10m AO2=AB2-BO2=202-102=300 ∴AO≈17.32m 花坛的两条小路长 AC=2AO ≈64.64m BD=2BO=20m 花坛的面积:S=0.5*AC*BD ≈346.40m2 学以致用1.已知菱形的周长是12cm,那么它的边长是______.2.菱形ABCD中∠ABC=60度,则∠BAC=_______.3cm60度3.菱形ABCD中,O是两条对角线的交点,已知AB=5cm,AO=4cm,求两对角线AC、BD的长。4.菱形ABCD中两条对角线的长分别是6cm和8cm,求菱形的周长和面积. 大显身手O 2、 用一张长为20cm宽为15cm的矩形纸片剪菱形纸片,问怎样剪,剪出的菱形面积最大?合作与交流方案1方案2方案3(1)菱形的四条边都相等.
(2)两条对角线互相垂直平分,每条对角线平分一组对角。总结归纳菱形的性质(1) 一组邻边相等的平行四边形是菱形。
(2)对角线互相垂直的平行四边形是菱形。
(3)四条边都相等的四边形是菱形。
总结归纳菱形的判别方法如图4-48,CD为Rt△ABC斜边AB上
的高,∠BAC的平分线交CD于E,交BC于F,FG⊥AB于G.求证:四边形EGFC为菱形.
已知:如图,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F.
求证:EF⊥AD; 大显身手6、在菱形ABCD中,AE⊥BC,AF⊥CD,E、F分别为BC,CD的中点,那么∠EAF的度数是( )A.75°B.60°C.45°D.30°B
二、经历探索菱形的性质和判别条件的过程,在操作活动和观察分析过程中养成主动探究的习惯,形成初步的审美意识,进一步了解和体会 说理的基本方法。
学习目标一组邻边相等的平行四边形叫做菱形。 一组邻
边相等菱形的定义在菱形ABCD中,对角线AC,BD相交于点O。
(1)图中那些线段是相等的?为什么?ABCDO观察与思考(2)图中那些角是相等的?为什么?ABCDO观察与思考(3)两条对角线有什么特定的位置关系,为什么?ABCDO观察与思考1、菱形是轴对称图形吗?如果是,那么它有几条对称轴?
观察与思考如何利用折纸、剪切的方法,既快又准确的剪出一个菱形的纸片?动手试一试1、两条等宽的纸条交叉重叠在一起,重叠的部分是菱形吗?为什么?动脑想一想有一组邻边相等的平行四边形叫做菱形;菱形的定义:一组邻边相等的平行四形是菱形。木工在做菱形的窗格时,总是保证四条边框一样长,你能说出其中的道理吗? 四条边都相等的平行四边形是菱形动脑想一想请观察刚才得到的菱形纸片上的折痕,再结合刚才的折纸操作,想一想其中的道理是什么?
对角线互相垂直的平行四边形是菱形。动脑想一想 他是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗? 如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?两组对边
分别平行情景创设我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,我们已经研究了一种特殊的平行四边形——矩形 ;这堂课还要研究另一种特殊的平行四边形——菱形菱形的性质:(1)菱形具有平行四边形的一切性质;(2)菱形的四条边都相等;(3)菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角;(4)菱形是轴对对称图形;也是中心对称图形;已知:菱形ABCD的对角线AC和BD相交于点O,如下图,证明:∵四边形ABCD是菱形在△ABD中,
又∵BO=DO∴AB=AD(菱形的四条边都相等)∴AC⊥BD,AC平分∠BAD同理: AC平分∠BCD;
BD平分∠ABC和∠ADC
求证:AC⊥BD ;
AC平分∠BAD和∠BCD ;BD平分∠ABC和∠ADC 命题:菱形的对角线互相垂直平分,
并且每一条对角线平分一组对角;相等的线段:相等的角:等腰三角形有:直角三角形有:全等三角形有:已知四边形ABCD是菱形AB=CD=AD=BC
OA=OC OB=OD∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8△ABC △ DBC △ACD △ABDRt△AOB Rt△BOC Rt△COD Rt△DOARt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACDABCDO12345678【菱形的面积公式】OES菱形=BC. AE思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积公式吗? 菱形的面积=底×高=对角线乘积的一半1、如图所示,平行四边形ABCD的两条对角线AC、BD相交于O。AB=√5,AO=2,OB=1
(1)AC与BD互相垂直吗?为什么?
(2)平行四边形ABCD是菱形吗?为什么?ABCDO典例与精练 ̄ ̄ ̄2、在菱形ABCD中,O是两条对角线交点。已知AB=5cm,AO=4cm,求对角线BD的长。ABCDO典例与精练合作与交流1、如图,菱形ABCD花坛的边长为20米,∠BAC=60.沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(分别精确到0.01米和0.01平方米)CABD解:∵花坛ABCD是菱形,∴AC⊥BD, ∠BAO=30. ∴BO=0.5*AB=0.5*20=10m AO2=AB2-BO2=202-102=300 ∴AO≈17.32m 花坛的两条小路长 AC=2AO ≈64.64m BD=2BO=20m 花坛的面积:S=0.5*AC*BD ≈346.40m2 学以致用1.已知菱形的周长是12cm,那么它的边长是______.2.菱形ABCD中∠ABC=60度,则∠BAC=_______.3cm60度3.菱形ABCD中,O是两条对角线的交点,已知AB=5cm,AO=4cm,求两对角线AC、BD的长。4.菱形ABCD中两条对角线的长分别是6cm和8cm,求菱形的周长和面积. 大显身手O 2、 用一张长为20cm宽为15cm的矩形纸片剪菱形纸片,问怎样剪,剪出的菱形面积最大?合作与交流方案1方案2方案3(1)菱形的四条边都相等.
(2)两条对角线互相垂直平分,每条对角线平分一组对角。总结归纳菱形的性质(1) 一组邻边相等的平行四边形是菱形。
(2)对角线互相垂直的平行四边形是菱形。
(3)四条边都相等的四边形是菱形。
总结归纳菱形的判别方法如图4-48,CD为Rt△ABC斜边AB上
的高,∠BAC的平分线交CD于E,交BC于F,FG⊥AB于G.求证:四边形EGFC为菱形.
已知:如图,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F.
求证:EF⊥AD; 大显身手6、在菱形ABCD中,AE⊥BC,AF⊥CD,E、F分别为BC,CD的中点,那么∠EAF的度数是( )A.75°B.60°C.45°D.30°B
