三、图形的运动——欣赏与设计(含答案)北师大版六年级数学下册(含答案)
文档属性
| 名称 | 三、图形的运动——欣赏与设计(含答案)北师大版六年级数学下册(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 613.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-20 16:35:26 | ||
图片预览

文档简介
三、图形的运动——欣赏与设计(含答案)
北师大版六年级数学下册
学校:___________姓名:___________班级:___________考号:___________
一、填空题
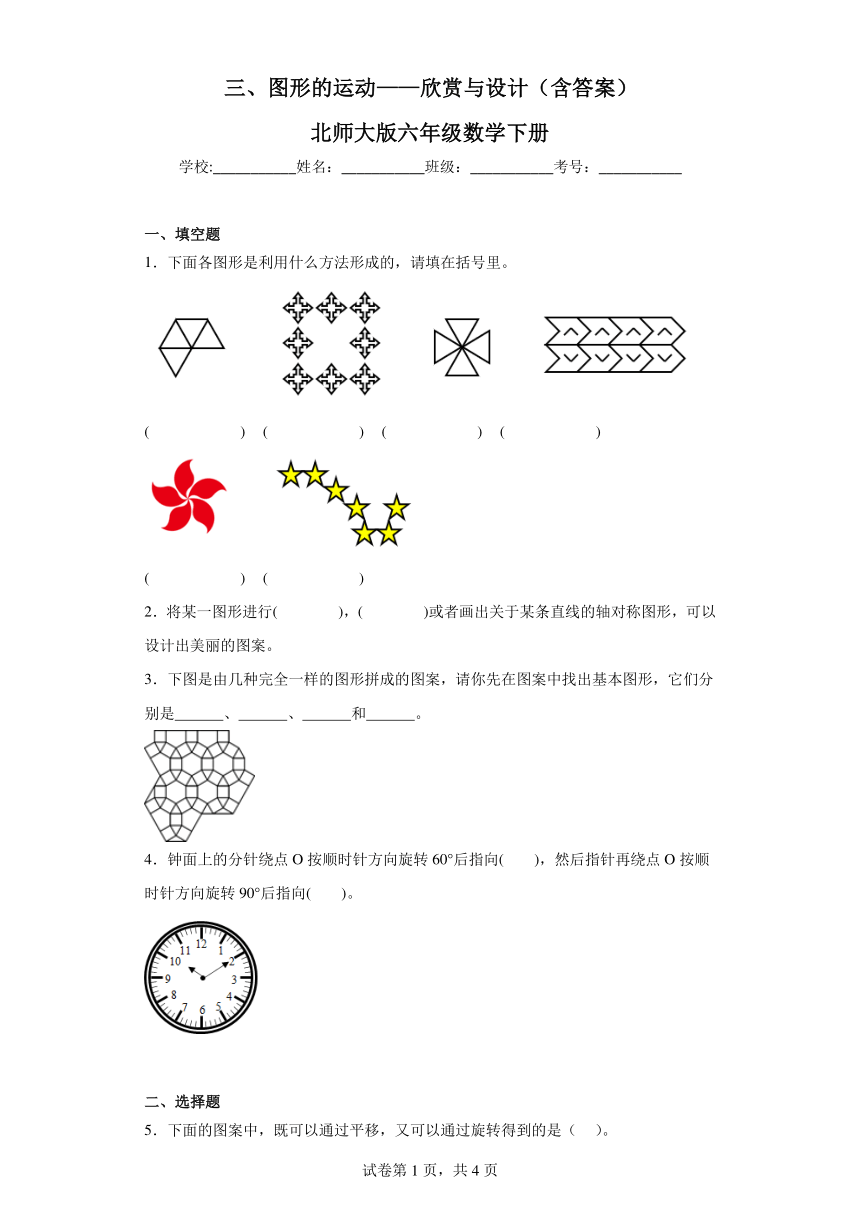
1.下面各图形是利用什么方法形成的,请填在括号里。
( ) ( ) ( ) ( )
( ) ( )
2.将某一图形进行( ),( )或者画出关于某条直线的轴对称图形,可以设计出美丽的图案。
3.下图是由几种完全一样的图形拼成的图案,请你先在图案中找出基本图形,它们分别是 、 、 和 。
4.钟面上的分针绕点O按顺时针方向旋转60°后指向( ),然后指针再绕点O按顺时针方向旋转90°后指向( )。
二、选择题
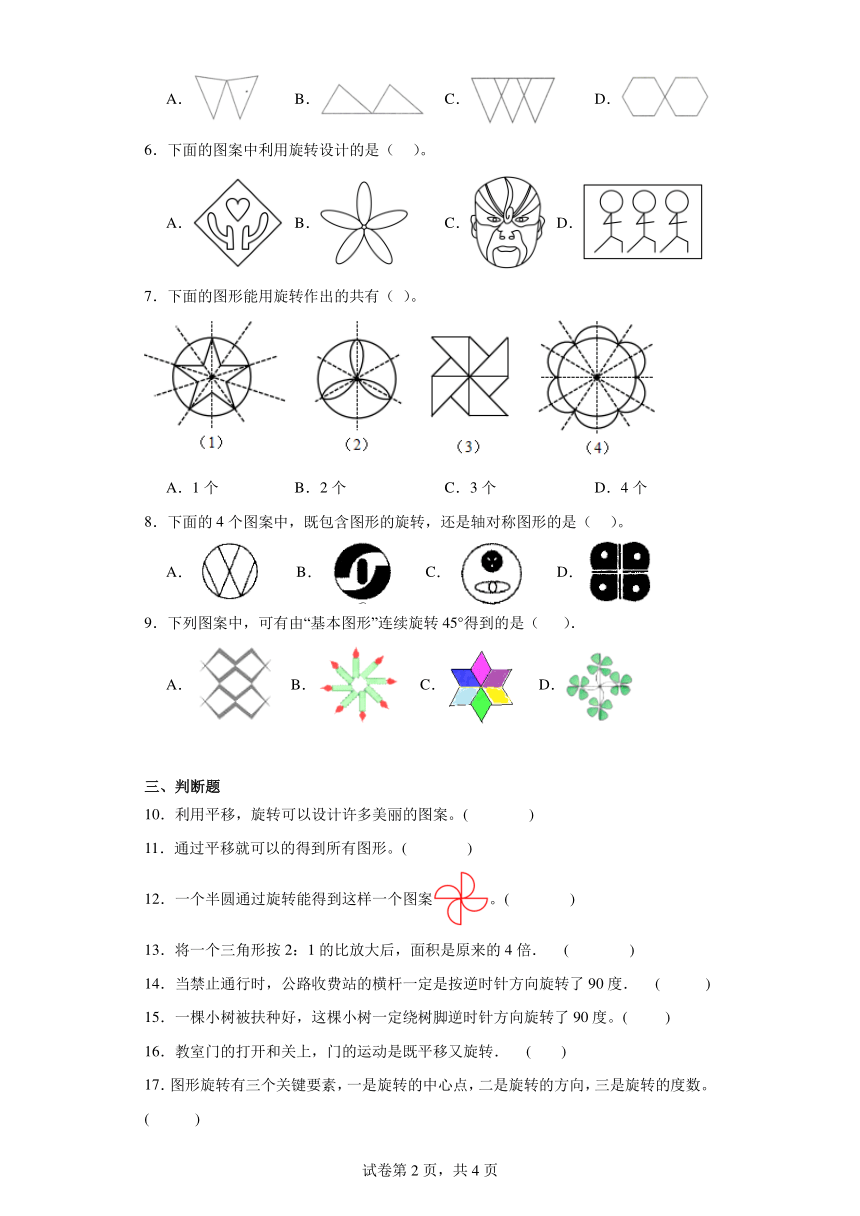
5.下面的图案中,既可以通过平移,又可以通过旋转得到的是( )。
A. B. C. D.
6.下面的图案中利用旋转设计的是( )。
A. B. C. D.
7.下面的图形能用旋转作出的共有( )。
A.1个 B.2个 C.3个 D.4个
8.下面的4个图案中,既包含图形的旋转,还是轴对称图形的是( )。
A. B. C. D.
9.下列图案中,可有由“基本图形”连续旋转45°得到的是( ).
A. B. C. D.
三、判断题
10.利用平移,旋转可以设计许多美丽的图案。( )
11.通过平移就可以的得到所有图形。( )
12.一个半圆通过旋转能得到这样一个图案。( )
13.将一个三角形按2:1的比放大后,面积是原来的4倍. ( )
14.当禁止通行时,公路收费站的横杆一定是按逆时针方向旋转了90度. ( )
15.一棵小树被扶种好,这棵小树一定绕树脚逆时针方向旋转了90度。( )
16.教室门的打开和关上,门的运动是既平移又旋转. ( )
17.图形旋转有三个关键要素,一是旋转的中心点,二是旋转的方向,三是旋转的度数。( )
四、解答题
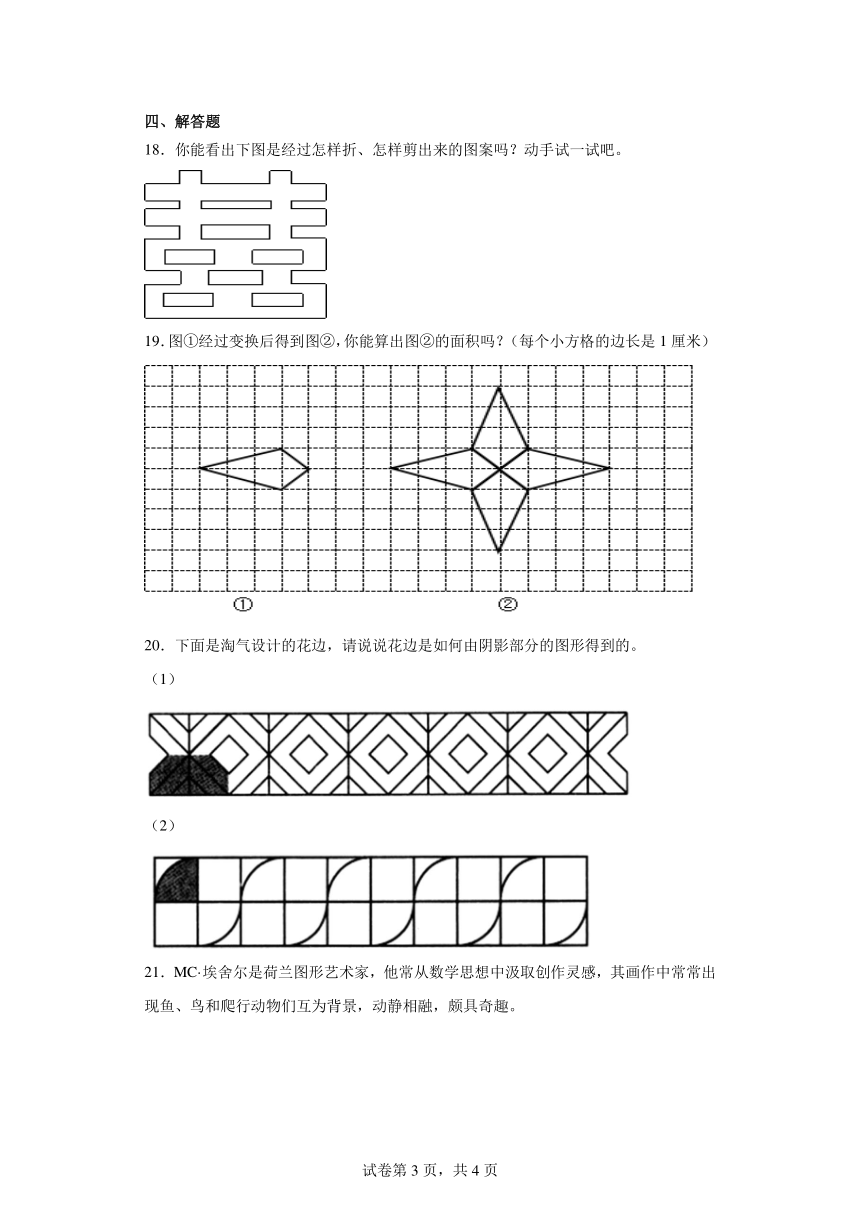
18.你能看出下图是经过怎样折、怎样剪出来的图案吗?动手试一试吧。
19.图①经过变换后得到图②,你能算出图②的面积吗?(每个小方格的边长是1厘米)
20.下面是淘气设计的花边,请说说花边是如何由阴影部分的图形得到的。
(1)
(2)
21.MC·埃舍尔是荷兰图形艺术家,他常从数学思想中汲取创作灵感,其画作中常常出现鱼、鸟和爬行动物们互为背景,动静相融,颇具奇趣。
(1)图1、图2中蕴含了我们学过的哪些图形的变换方式?
(2)请你当一回图形设计师,完成图案设计,并写出你的设计方案时运用到哪些图形的变换方式。我用到的图形变换方式有:( )。
22.张小明同学为班级“学习专栏”设计了报头图案,并用文字说明图案的含义,如图①请你用基本的几何图形(如直线、射线、线段、角、三角形、平行四边形、长方形、正方形等)中若干个为“环保专栏”在下图框中设计一个报头图案,并简要说明图案的含义。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1. 旋转 平移 旋转 轴对称 旋转 平移
2. 平移 旋转
3. 六边形 五边形 正方形 三角形
根据题意将图整理如下:
基本图形有六边形、五边形、正方形、填空题。
4. 4 7
5.D
6.B
7.D
8.D
9.B
10.√
11.×
12.√
13.√
14.×
15.×
【详解】一棵小树被扶种好,这棵小树可能绕树脚逆时针方向旋转了90度,也可能绕树脚顺时针方向旋转了90度。
16.×
17.√
18.如图:
19.4×1÷2×2=4(平方厘米)
4×4=16(平方厘米)
答:图②的面积是16平方厘米。
20.1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出阴影部分的关键对称点,依次连接涂色即可;然后将轴对称图形分别向右平移5次,即可得到对应的花边。
(2)先根据旋转的概念,把阴影部分绕中心点按顺时针(或逆时针)方向旋转180°,再将两部分依次向右平移四次,即可得到对应的花边。
21.(1)通过观察可知相同颜色的图形,通过平移可以得到,不同颜色的图形,通过旋转可以得到。所以图1蕴含了我们学过的平移和旋转的变换方式。图2可以通过轴对称得到,图2的上半部分和下半部分通过中间的直线可以重合,所以是轴对称图形,可以通过轴对称得到。所以图2蕴含了我们学过的轴对称变换方式。
(2)如图:
我用到的图形的变换方式有旋转。
22.
含义:请走近垃圾箱,将垃圾放入箱内。
答案第1页,共2页
答案第1页,共2页
北师大版六年级数学下册
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.下面各图形是利用什么方法形成的,请填在括号里。
( ) ( ) ( ) ( )
( ) ( )
2.将某一图形进行( ),( )或者画出关于某条直线的轴对称图形,可以设计出美丽的图案。
3.下图是由几种完全一样的图形拼成的图案,请你先在图案中找出基本图形,它们分别是 、 、 和 。
4.钟面上的分针绕点O按顺时针方向旋转60°后指向( ),然后指针再绕点O按顺时针方向旋转90°后指向( )。
二、选择题
5.下面的图案中,既可以通过平移,又可以通过旋转得到的是( )。
A. B. C. D.
6.下面的图案中利用旋转设计的是( )。
A. B. C. D.
7.下面的图形能用旋转作出的共有( )。
A.1个 B.2个 C.3个 D.4个
8.下面的4个图案中,既包含图形的旋转,还是轴对称图形的是( )。
A. B. C. D.
9.下列图案中,可有由“基本图形”连续旋转45°得到的是( ).
A. B. C. D.
三、判断题
10.利用平移,旋转可以设计许多美丽的图案。( )
11.通过平移就可以的得到所有图形。( )
12.一个半圆通过旋转能得到这样一个图案。( )
13.将一个三角形按2:1的比放大后,面积是原来的4倍. ( )
14.当禁止通行时,公路收费站的横杆一定是按逆时针方向旋转了90度. ( )
15.一棵小树被扶种好,这棵小树一定绕树脚逆时针方向旋转了90度。( )
16.教室门的打开和关上,门的运动是既平移又旋转. ( )
17.图形旋转有三个关键要素,一是旋转的中心点,二是旋转的方向,三是旋转的度数。( )
四、解答题
18.你能看出下图是经过怎样折、怎样剪出来的图案吗?动手试一试吧。
19.图①经过变换后得到图②,你能算出图②的面积吗?(每个小方格的边长是1厘米)
20.下面是淘气设计的花边,请说说花边是如何由阴影部分的图形得到的。
(1)
(2)
21.MC·埃舍尔是荷兰图形艺术家,他常从数学思想中汲取创作灵感,其画作中常常出现鱼、鸟和爬行动物们互为背景,动静相融,颇具奇趣。
(1)图1、图2中蕴含了我们学过的哪些图形的变换方式?
(2)请你当一回图形设计师,完成图案设计,并写出你的设计方案时运用到哪些图形的变换方式。我用到的图形变换方式有:( )。
22.张小明同学为班级“学习专栏”设计了报头图案,并用文字说明图案的含义,如图①请你用基本的几何图形(如直线、射线、线段、角、三角形、平行四边形、长方形、正方形等)中若干个为“环保专栏”在下图框中设计一个报头图案,并简要说明图案的含义。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1. 旋转 平移 旋转 轴对称 旋转 平移
2. 平移 旋转
3. 六边形 五边形 正方形 三角形
根据题意将图整理如下:
基本图形有六边形、五边形、正方形、填空题。
4. 4 7
5.D
6.B
7.D
8.D
9.B
10.√
11.×
12.√
13.√
14.×
15.×
【详解】一棵小树被扶种好,这棵小树可能绕树脚逆时针方向旋转了90度,也可能绕树脚顺时针方向旋转了90度。
16.×
17.√
18.如图:
19.4×1÷2×2=4(平方厘米)
4×4=16(平方厘米)
答:图②的面积是16平方厘米。
20.1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出阴影部分的关键对称点,依次连接涂色即可;然后将轴对称图形分别向右平移5次,即可得到对应的花边。
(2)先根据旋转的概念,把阴影部分绕中心点按顺时针(或逆时针)方向旋转180°,再将两部分依次向右平移四次,即可得到对应的花边。
21.(1)通过观察可知相同颜色的图形,通过平移可以得到,不同颜色的图形,通过旋转可以得到。所以图1蕴含了我们学过的平移和旋转的变换方式。图2可以通过轴对称得到,图2的上半部分和下半部分通过中间的直线可以重合,所以是轴对称图形,可以通过轴对称得到。所以图2蕴含了我们学过的轴对称变换方式。
(2)如图:
我用到的图形的变换方式有旋转。
22.
含义:请走近垃圾箱,将垃圾放入箱内。
答案第1页,共2页
答案第1页,共2页
