高中数学5.3简单的三角恒等变换导学案 湘教版必修2
文档属性
| 名称 | 高中数学5.3简单的三角恒等变换导学案 湘教版必修2 |

|
|
| 格式 | zip | ||
| 文件大小 | 64.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-17 13:29:11 | ||
图片预览

文档简介
5.3《简单的三角恒等变换》导学案
班级: 姓名:
【学习目标】: 通过例题的解答,促进学 ( http: / / www.21cnjy.com )生形成对解题过程中如何选择公式,如何根据问题的条件进行公式变形,以及变换过程中体现的换元。逆向使用公式等数学思想方法的认识,
从而加深理解变换思想,提高推理能力。
(课前)【知识链接】: 辅助角公式
(其中)
(课中)1.合作探究:
三角恒等变换的常用方法:能灵活利用公式对三角函数式进行变形,必须注意三变:变名,变次,变角。
变名
求函数的周期,最大值和最小值。
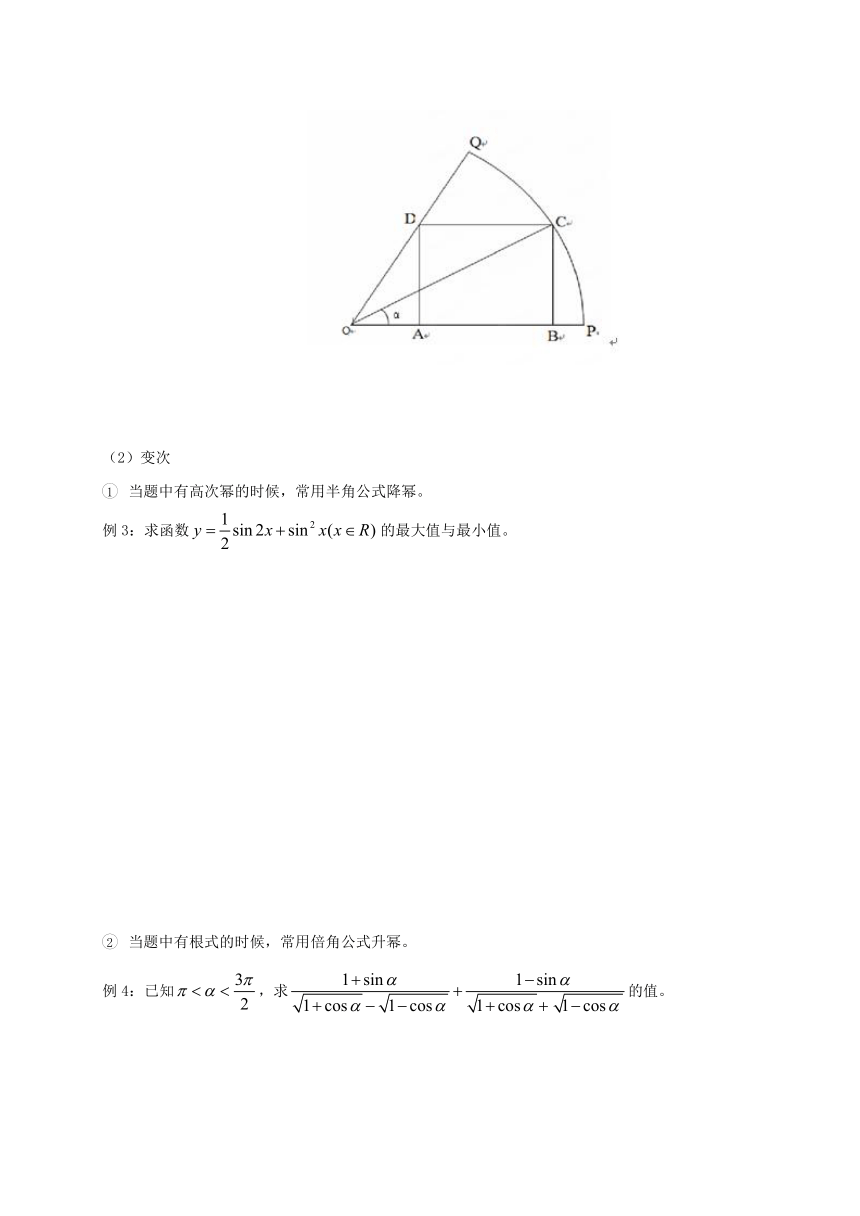
已知是半径为1,圆心角为的扇形,是扇形弧上的动点,是扇形的内接矩形,记,求当角取何值时,矩形的面积最大?并求这个最大面积。
( http: / / www.21cnjy.com )
(2)变次
当题中有高次幂的时候,常用半角公式降幂。
例3:求函数的最大值与最小值。
当题中有根式的时候,常用倍角公式升幂。
例4:已知,求的值。
变角:
例6:求证:
【交流展示】:
1.求值: ( )
A2 B-2 C D
2.已知则的值是 ( )
A. B C D
3.函数是 ( )
A周期为的偶函数 B周期为的奇函数
C周期为的偶函数 D周期为的奇函数
【当堂检测】:
1.若函数与函数和的图象分别交于M,N两点,则MN长度的最大值为 ( )
A1 B C D2
2.函数是 ( )
A周期为的偶函数 B周期为的非奇非偶函数
C周期为的偶函数 D周期为的非奇非偶函数
3.已知函数的最小正周期为。
(1)求的值。
(2)求函数在区间上的取值范围。
4.化简.
5.求证
自我总结:
班级: 姓名:
【学习目标】: 通过例题的解答,促进学 ( http: / / www.21cnjy.com )生形成对解题过程中如何选择公式,如何根据问题的条件进行公式变形,以及变换过程中体现的换元。逆向使用公式等数学思想方法的认识,
从而加深理解变换思想,提高推理能力。
(课前)【知识链接】: 辅助角公式
(其中)
(课中)1.合作探究:
三角恒等变换的常用方法:能灵活利用公式对三角函数式进行变形,必须注意三变:变名,变次,变角。
变名
求函数的周期,最大值和最小值。
已知是半径为1,圆心角为的扇形,是扇形弧上的动点,是扇形的内接矩形,记,求当角取何值时,矩形的面积最大?并求这个最大面积。
( http: / / www.21cnjy.com )
(2)变次
当题中有高次幂的时候,常用半角公式降幂。
例3:求函数的最大值与最小值。
当题中有根式的时候,常用倍角公式升幂。
例4:已知,求的值。
变角:
例6:求证:
【交流展示】:
1.求值: ( )
A2 B-2 C D
2.已知则的值是 ( )
A. B C D
3.函数是 ( )
A周期为的偶函数 B周期为的奇函数
C周期为的偶函数 D周期为的奇函数
【当堂检测】:
1.若函数与函数和的图象分别交于M,N两点,则MN长度的最大值为 ( )
A1 B C D2
2.函数是 ( )
A周期为的偶函数 B周期为的非奇非偶函数
C周期为的偶函数 D周期为的非奇非偶函数
3.已知函数的最小正周期为。
(1)求的值。
(2)求函数在区间上的取值范围。
4.化简.
5.求证
自我总结:
