第三单元:简易方程(二)单元复习课件(共26张PPT)沪教版五年级数学下册
文档属性
| 名称 | 第三单元:简易方程(二)单元复习课件(共26张PPT)沪教版五年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
简易方程(二)单元复习
沪教版五年级数学下册
列方程解应用题(三)
列方程解应用题(四)
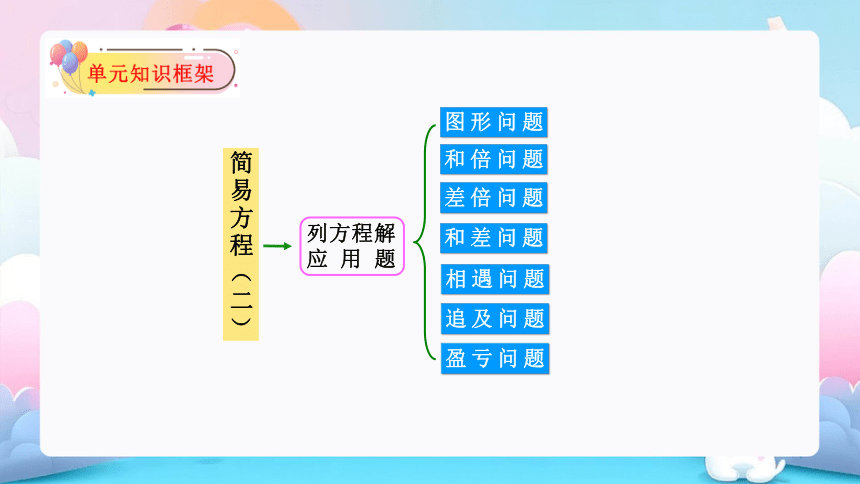
简易方程(二)
图形问题
列方程解应用题
和倍问题
差倍问题
和差问题
相遇问题
追及问题
盈亏问题
1、列方程解应用题的关键:
找未知量和已知量之间的等量关系。
2、列方程解应用题的一般步骤:
(1)用字母表示未知数,并根据题意,用未知数来表示相关的量;
(2)找出未知量与已知量之间的等量关系,并列出方程;
(3)解方程;
(4)检验并写出答句。
【例1】一块梯形稻田的面积是630平方米,上底比下底少10米,高是15米,则下底长是多少米?
图形问题
梯形的面积=(上底+下底)×高÷2
解:设下底长为x米,则上底长为(x-10)米。
(x+x-10)×15÷2=630
2x-10=630×2÷15
2x-10=84
2x=94
x=47
答:下底长是47米。
【例2】用一根长是28厘米铁丝围出的一个长方形,长方形的长比宽长6厘米,那么长方形的宽是多少厘米?
长方形的周长=2×(长+宽)
解:设长方形的宽为x厘米,则长为(x+6)厘米。
2×(x+x+6)=28
2x+6=28÷2
2x=14-6
x=8÷2
x=4
答:长方形的宽是4厘米。
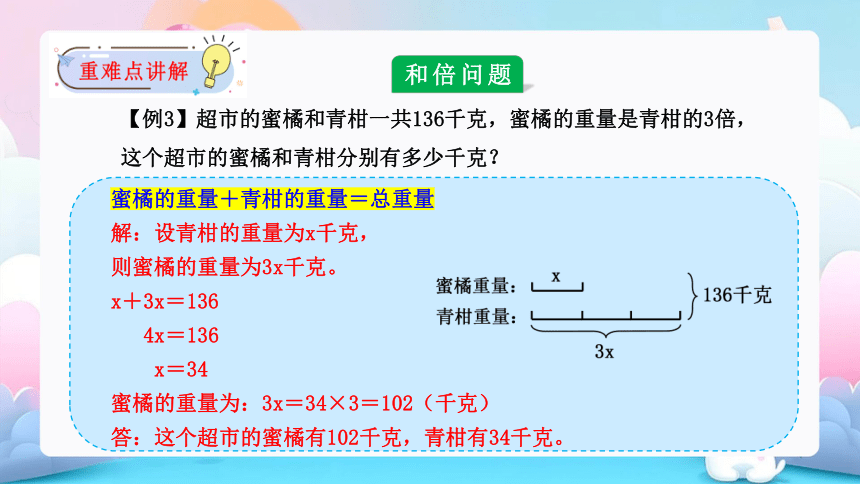
【例3】超市的蜜橘和青柑一共136千克,蜜橘的重量是青柑的3倍,这个超市的蜜橘和青柑分别有多少千克?
和倍问题
蜜橘的重量+青柑的重量=总重量
解:设青柑的重量为x千克,
则蜜橘的重量为3x千克。
x+3x=136
4x=136
x=34
蜜橘的重量为:3x=34×3=102(千克)
答:这个超市的蜜橘有102千克,青柑有34千克。
【例4】吴奶奶家里养了30只兔子,其中白兔只数是黑兔的4倍,吴奶奶家养的白兔和黑兔分别有多少只?
白兔数量+黑兔数量=兔子总数
解:设设黑兔的数量为x只,所以白兔的数量为4x只。
x+4x=30
5x=30
x=6
白兔的数量为:4x=6×4=24(只)
答:吴奶奶家养的白兔有24只,黑兔有6只。
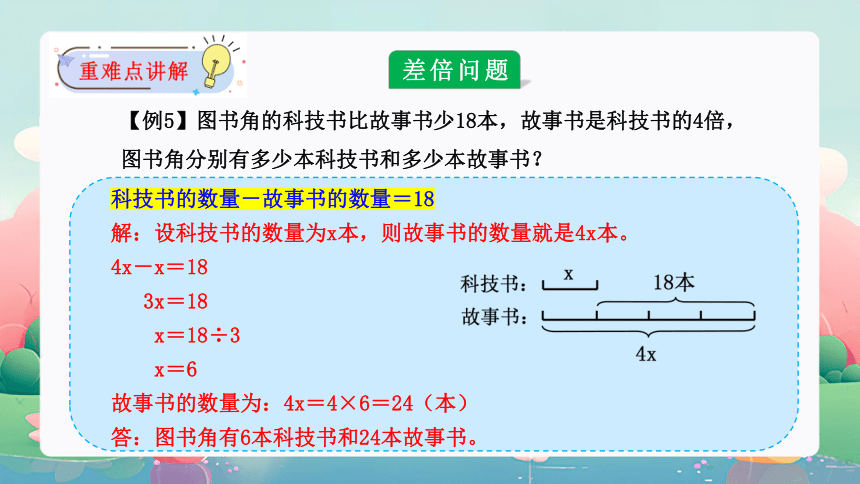
【例5】图书角的科技书比故事书少18本,故事书是科技书的4倍,图书角分别有多少本科技书和多少本故事书?
科技书的数量-故事书的数量=18
解:设科技书的数量为x本,则故事书的数量就是4x本。
4x-x=18
3x=18
x=18÷3
x=6
故事书的数量为:4x=4×6=24(本)
答:图书角有6本科技书和24本故事书。
差倍问题
【例6】爸爸比儿子大24岁,今年爸爸的年龄是儿子年龄的3倍,则父子二人今年分别是多少岁?
今年爸爸的年龄-今年儿子的年龄=24
解:设儿子今年x岁,则爸爸今年3x岁。
3x-x=24
2x=24
x=24÷2
x=12
爸爸今年:3x=3×12=36(岁)
答:儿子今年12岁,爸爸今年36岁。
【例7】两筐土豆一共重90千克,第一筐比第二筐少20千克,两筐土豆分别重多少千克?
第一筐土豆+第二筐土豆=土豆总重量
解:第一筐土豆重量为x千克,则第二筐土豆重量为(x+20)千克。
x+(x+20)=90
2x+20=90
2x=70
x=35
第二筐土豆重量为:x+20=35+20=55(千克)
答:第一筐土豆重35千克,第二筐土豆重55千克。
和差问题
【例8】甲、乙两人同时以相同的速度打字,两人2分钟一共打270个字,甲每分钟比乙多打15个字。甲、乙两人每分钟分别打多少个字?
甲每分钟打的总字数+乙每分钟打的字数=两人每分钟打的总字数
解:甲每分钟打x个字,则乙每分钟打(x-15)个字。
x+(x-15)=270÷2
2x-15=135
2x=150
x=75
乙每分钟打:x-15=75+15=55(个)
答:甲每分钟打75个字,则乙每分钟打55个字。
【例9】甲、乙两车同时从相距270千米的两地出发相向而行,甲车每小时行驶65千米,乙车每小时行驶70千米,两车经过多少个小时相遇?
解法一:甲车路程+乙车路程=总路程
解:设两车经过x个小时相遇。
65x+70x=270
135x=270
x=270÷135
x=2
答:两车经过2个小时相遇。
相遇问题
【例9】甲、乙两车同时从相距270千米的两地出发相向而行,甲车每小时行驶65千米,乙车每小时行驶70千米,两车经过多少个小时相遇?
解法二:(甲车速度+乙车速度)×相遇时间=总路程
解:设两车经过x个小时相遇。
(65+70)×x=270
135x=270
x=270÷135
x=2
答:两车经过2个小时相遇。
【例10】A、B两地的公路长615千米。两辆汽车从A、B两地相对开出,甲车每小时行驶75千米,乙车每小时行驶80千米。甲车开出2小时后,乙车才出发,再经过多少个小时两车相遇?
甲车第一段走的路程+甲车第二段走的路程+乙车路程=总路程
解:设两车再经过x个小时相遇。
75×2+75x+80x=615
150+155x=615
155x=465
x=3
答:两车经过3个小时相遇。
【例11】乙车以平均每小时90千米的速度去追前方相距60千米的甲车,已知甲车平均平均每小时行驶75千米,乙车多少小时后追上甲车?
解法一:乙车的路程-甲车后行的路程=甲车先行的路程
解:设乙车要x小时才能追上甲车。
90x-75x=60
15x=60
x=4
答:乙车要4小时才能追上甲车。
追及问题
解法二:(乙车的速度-甲车的速度)×追及时间=追及路程
解:设甲要x小时才能追上乙。
(90-75)x=60
15x=60
x=4
答:乙车要4小时才能追上甲车。
【例11】乙车以平均每小时90千米的速度去追前方相距60千米的甲车,已知甲车平均平均每小时行驶75千米,乙车多少小时后追上甲车?
【例12】甲、乙两人从同一地点出发,同向而行,甲每小时走3千米,乙每小时走5千米,甲先出发2小时,乙再出发追赶甲,乙要多少小时才能追上甲?
乙的路程-甲后行的路程=甲先行的路程
解:设乙车要x小时才能追上甲车。
5x-3x=2×3
2x=6
x=3
答:乙要3小时才能追上甲。
【例13】饲养员把一堆桃子分给一群猴子。如果每只猴子分6个桃子,刚好分完;如果每只猴子分8个桃子,则还有2只猴子没分到桃子。一共有多少只猴子?
每只猴子分6个桃子的桃子总数=每只猴子分8个桃子的桃子总数
解:设有x只猴子。
6x=8(x-2)
6x=8x-16
2x=16
x=8
答:一共有8只猴子。
盈亏问题
【例14】同学们去植树,如果每人种3棵,还剩下13棵树苗;如果每人种5棵,就缺少7棵树苗。求有多少个同学去植树?
每人种3棵的树苗总数=每人种5棵的树苗总数
解:设有x个同学去植树。
3x+13=5x-7
5x-3x=13+7
2x=20
x=10
答:有10个同学去植树。
1、甲、乙两辆汽车从相距410千米两地同时相向开出,经过2.5小时在途中相遇。已知甲车每小时行驶78千米,乙车每小时行驶多少千米?
(甲车速度+乙车速度)×相遇时间=总路程
解:设乙车每小时行驶x千米。
(78+x)×2.5=410
195+2.5x=410
2.5x=215
x=86
答:乙车每小时行驶86千米。
2、一个边长为12厘米的正方形与一个长方形的面积相等,已知长方形的宽是8厘米,长方形的长是多少厘米?
长方形的面积=正方形的面积
解:设长方形的长是x厘米。
8x=12×12
8x=144
x=144÷8
x=18
答:长方形的长是18厘米。
3、果园里有荔枝树472棵,比龙眼树的3倍少29棵,果园里有多少棵龙眼树?
龙眼树的棵树×3-29=荔枝树的棵树
解:设果园里有x棵龙眼树。
3x-29=472
3x=472+29
3x=501
x=167
答:果园里有167棵龙眼树。
4、五(1)班有45人,其中男生人数比女生多7人,那么男生和女生各有多少人?
男生人数+女生人数=学生总人数
解:设女生有x人,则男生有(x+7)人。
(x+7)+x=45
2x+7=45
2x=38
x=19
男生有:x+7=19+7=26(人)
答:男生有26人,女生有19人。
5、一块三角形田地的高是底的1.5倍,且高比底长20米,那么这块三角形田地的面积是多少平方米?
高的长度-底的长度=多出的长度
解:设底长x米,那么高长1.5x米。
1.5x-x=20
0.5x=20
x=40
高长:1.5x=1.5×40=60(米)
40×60÷2=1200(米)
答:这块三角形田地的面积是1200平方米。
每一份努力,都将在学习中得到最好的回报。加油!
简易方程(二)单元复习
沪教版五年级数学下册
列方程解应用题(三)
列方程解应用题(四)
简易方程(二)
图形问题
列方程解应用题
和倍问题
差倍问题
和差问题
相遇问题
追及问题
盈亏问题
1、列方程解应用题的关键:
找未知量和已知量之间的等量关系。
2、列方程解应用题的一般步骤:
(1)用字母表示未知数,并根据题意,用未知数来表示相关的量;
(2)找出未知量与已知量之间的等量关系,并列出方程;
(3)解方程;
(4)检验并写出答句。
【例1】一块梯形稻田的面积是630平方米,上底比下底少10米,高是15米,则下底长是多少米?
图形问题
梯形的面积=(上底+下底)×高÷2
解:设下底长为x米,则上底长为(x-10)米。
(x+x-10)×15÷2=630
2x-10=630×2÷15
2x-10=84
2x=94
x=47
答:下底长是47米。
【例2】用一根长是28厘米铁丝围出的一个长方形,长方形的长比宽长6厘米,那么长方形的宽是多少厘米?
长方形的周长=2×(长+宽)
解:设长方形的宽为x厘米,则长为(x+6)厘米。
2×(x+x+6)=28
2x+6=28÷2
2x=14-6
x=8÷2
x=4
答:长方形的宽是4厘米。
【例3】超市的蜜橘和青柑一共136千克,蜜橘的重量是青柑的3倍,这个超市的蜜橘和青柑分别有多少千克?
和倍问题
蜜橘的重量+青柑的重量=总重量
解:设青柑的重量为x千克,
则蜜橘的重量为3x千克。
x+3x=136
4x=136
x=34
蜜橘的重量为:3x=34×3=102(千克)
答:这个超市的蜜橘有102千克,青柑有34千克。
【例4】吴奶奶家里养了30只兔子,其中白兔只数是黑兔的4倍,吴奶奶家养的白兔和黑兔分别有多少只?
白兔数量+黑兔数量=兔子总数
解:设设黑兔的数量为x只,所以白兔的数量为4x只。
x+4x=30
5x=30
x=6
白兔的数量为:4x=6×4=24(只)
答:吴奶奶家养的白兔有24只,黑兔有6只。
【例5】图书角的科技书比故事书少18本,故事书是科技书的4倍,图书角分别有多少本科技书和多少本故事书?
科技书的数量-故事书的数量=18
解:设科技书的数量为x本,则故事书的数量就是4x本。
4x-x=18
3x=18
x=18÷3
x=6
故事书的数量为:4x=4×6=24(本)
答:图书角有6本科技书和24本故事书。
差倍问题
【例6】爸爸比儿子大24岁,今年爸爸的年龄是儿子年龄的3倍,则父子二人今年分别是多少岁?
今年爸爸的年龄-今年儿子的年龄=24
解:设儿子今年x岁,则爸爸今年3x岁。
3x-x=24
2x=24
x=24÷2
x=12
爸爸今年:3x=3×12=36(岁)
答:儿子今年12岁,爸爸今年36岁。
【例7】两筐土豆一共重90千克,第一筐比第二筐少20千克,两筐土豆分别重多少千克?
第一筐土豆+第二筐土豆=土豆总重量
解:第一筐土豆重量为x千克,则第二筐土豆重量为(x+20)千克。
x+(x+20)=90
2x+20=90
2x=70
x=35
第二筐土豆重量为:x+20=35+20=55(千克)
答:第一筐土豆重35千克,第二筐土豆重55千克。
和差问题
【例8】甲、乙两人同时以相同的速度打字,两人2分钟一共打270个字,甲每分钟比乙多打15个字。甲、乙两人每分钟分别打多少个字?
甲每分钟打的总字数+乙每分钟打的字数=两人每分钟打的总字数
解:甲每分钟打x个字,则乙每分钟打(x-15)个字。
x+(x-15)=270÷2
2x-15=135
2x=150
x=75
乙每分钟打:x-15=75+15=55(个)
答:甲每分钟打75个字,则乙每分钟打55个字。
【例9】甲、乙两车同时从相距270千米的两地出发相向而行,甲车每小时行驶65千米,乙车每小时行驶70千米,两车经过多少个小时相遇?
解法一:甲车路程+乙车路程=总路程
解:设两车经过x个小时相遇。
65x+70x=270
135x=270
x=270÷135
x=2
答:两车经过2个小时相遇。
相遇问题
【例9】甲、乙两车同时从相距270千米的两地出发相向而行,甲车每小时行驶65千米,乙车每小时行驶70千米,两车经过多少个小时相遇?
解法二:(甲车速度+乙车速度)×相遇时间=总路程
解:设两车经过x个小时相遇。
(65+70)×x=270
135x=270
x=270÷135
x=2
答:两车经过2个小时相遇。
【例10】A、B两地的公路长615千米。两辆汽车从A、B两地相对开出,甲车每小时行驶75千米,乙车每小时行驶80千米。甲车开出2小时后,乙车才出发,再经过多少个小时两车相遇?
甲车第一段走的路程+甲车第二段走的路程+乙车路程=总路程
解:设两车再经过x个小时相遇。
75×2+75x+80x=615
150+155x=615
155x=465
x=3
答:两车经过3个小时相遇。
【例11】乙车以平均每小时90千米的速度去追前方相距60千米的甲车,已知甲车平均平均每小时行驶75千米,乙车多少小时后追上甲车?
解法一:乙车的路程-甲车后行的路程=甲车先行的路程
解:设乙车要x小时才能追上甲车。
90x-75x=60
15x=60
x=4
答:乙车要4小时才能追上甲车。
追及问题
解法二:(乙车的速度-甲车的速度)×追及时间=追及路程
解:设甲要x小时才能追上乙。
(90-75)x=60
15x=60
x=4
答:乙车要4小时才能追上甲车。
【例11】乙车以平均每小时90千米的速度去追前方相距60千米的甲车,已知甲车平均平均每小时行驶75千米,乙车多少小时后追上甲车?
【例12】甲、乙两人从同一地点出发,同向而行,甲每小时走3千米,乙每小时走5千米,甲先出发2小时,乙再出发追赶甲,乙要多少小时才能追上甲?
乙的路程-甲后行的路程=甲先行的路程
解:设乙车要x小时才能追上甲车。
5x-3x=2×3
2x=6
x=3
答:乙要3小时才能追上甲。
【例13】饲养员把一堆桃子分给一群猴子。如果每只猴子分6个桃子,刚好分完;如果每只猴子分8个桃子,则还有2只猴子没分到桃子。一共有多少只猴子?
每只猴子分6个桃子的桃子总数=每只猴子分8个桃子的桃子总数
解:设有x只猴子。
6x=8(x-2)
6x=8x-16
2x=16
x=8
答:一共有8只猴子。
盈亏问题
【例14】同学们去植树,如果每人种3棵,还剩下13棵树苗;如果每人种5棵,就缺少7棵树苗。求有多少个同学去植树?
每人种3棵的树苗总数=每人种5棵的树苗总数
解:设有x个同学去植树。
3x+13=5x-7
5x-3x=13+7
2x=20
x=10
答:有10个同学去植树。
1、甲、乙两辆汽车从相距410千米两地同时相向开出,经过2.5小时在途中相遇。已知甲车每小时行驶78千米,乙车每小时行驶多少千米?
(甲车速度+乙车速度)×相遇时间=总路程
解:设乙车每小时行驶x千米。
(78+x)×2.5=410
195+2.5x=410
2.5x=215
x=86
答:乙车每小时行驶86千米。
2、一个边长为12厘米的正方形与一个长方形的面积相等,已知长方形的宽是8厘米,长方形的长是多少厘米?
长方形的面积=正方形的面积
解:设长方形的长是x厘米。
8x=12×12
8x=144
x=144÷8
x=18
答:长方形的长是18厘米。
3、果园里有荔枝树472棵,比龙眼树的3倍少29棵,果园里有多少棵龙眼树?
龙眼树的棵树×3-29=荔枝树的棵树
解:设果园里有x棵龙眼树。
3x-29=472
3x=472+29
3x=501
x=167
答:果园里有167棵龙眼树。
4、五(1)班有45人,其中男生人数比女生多7人,那么男生和女生各有多少人?
男生人数+女生人数=学生总人数
解:设女生有x人,则男生有(x+7)人。
(x+7)+x=45
2x+7=45
2x=38
x=19
男生有:x+7=19+7=26(人)
答:男生有26人,女生有19人。
5、一块三角形田地的高是底的1.5倍,且高比底长20米,那么这块三角形田地的面积是多少平方米?
高的长度-底的长度=多出的长度
解:设底长x米,那么高长1.5x米。
1.5x-x=20
0.5x=20
x=40
高长:1.5x=1.5×40=60(米)
40×60÷2=1200(米)
答:这块三角形田地的面积是1200平方米。
每一份努力,都将在学习中得到最好的回报。加油!
