高中数学 4.6向量的应用学案 湘教版必修2
文档属性
| 名称 | 高中数学 4.6向量的应用学案 湘教版必修2 |
|
|
| 格式 | zip | ||
| 文件大小 | 44.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-17 16:40:26 | ||
图片预览


文档简介
4.6向量的应用学案
教学目标:
1.经历用向量方法解决某些简单的几何问题、力学问题的过程,体会向量是一种数学工具,发展学生运算能力和解决实际问题的能力;
2.运用向量的有关知识对物理中的问题进行相关分析和计算,并在这个过程中培养学生探究问题和解决问题的能力.
教学重点:
运用向量的有关知识对物理中的问题进行相关分析和计算,用向量方法解决实际问题的基本方法;向量法解决几何问题的“三步曲”.
教学难点:
实际问题转化为向量问题,体现向量的工具作 ( http: / / www.21cnjy.com )用.用向量的方法解决某些简单的平面几何问题、力学问题与其它一些实际问题,体会向量在几何、物理中的应用.
教学方法:
启发式教学.
教学过程:
一、情景创设
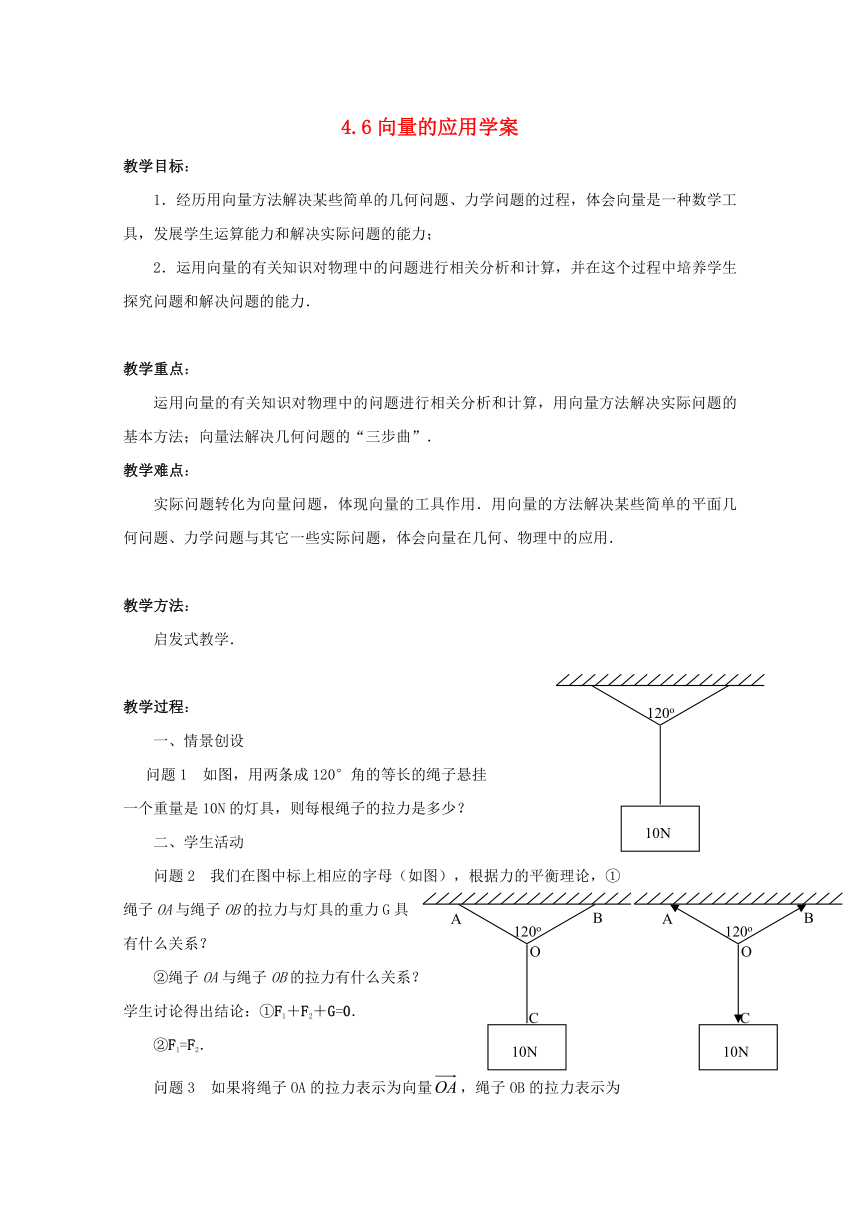
问题1 如图,用两条成120°角的等长的绳子悬挂
一个重量是10N的灯具,则每根绳子的拉力是多少?
二、学生活动
问题2 我们在图中标上相应的字母(如图),根据力的平衡理论,①绳子OA与绳子OB的拉力与灯具的重力G具有什么关系?
②绳子OA与绳子OB的拉力有什么关系?
学生讨论得出结论:①F1+F2+G=0.
②F1=F2.
问题3 如果将绳子OA的拉力表示为向量,绳子OB的拉力表示为向量,重力表示为向量,则向量、、之间有什么关系?
学生讨论得出结论:++=.这样物理问题就与数学中的向量产生了联系
三、建构数学
问题4 你能否根据以上信息,将这个物理问题编写成一个数学问题?你能解决这个问题吗?
学生讨论,教师整理,形成数学问题:已知向量、之间的夹角为120o,且向量的模等于向量的模,向量的模为10,求向量、的模.
学生讨论解决问题:
过A,B两点分别作OB、OA的平行线,相交于D点,则四边形OADB是菱形,连接OD,则OD=||=10,因为OA=OB=AD=BD,且∠AOB=120o,所以ΔOAD是等边三角形,
所以OA=AD=OD=10,即||=10,||=10.亦即每根绳子的拉力都是10N.
变题:在汽车站或火车站我们常见:两个人共提一个旅行包,若包重20N,还需什么条件,你能求每一个人手臂的拉力?
小结:(由学生讨论,教师整理)1.利用向量 ( http: / / www.21cnjy.com )解决物理问题的基本步骤:①问题转化,即把物理问题转化为数学问题;②建立模型,即建立以向量为载体的数学模型;③求解参数,即求向量的模、夹角、数量积等;④回答问题,即把所得的数学结论回归到物理问题.
2.用向量知识解决物理问题时,要注意数形结合.一般先要作出向量示意图,必要时可建立直角坐标系,再通过解三角形或坐标运算,求有关量的值.
四、数学应用
1.例题.
例1 如图(1)所示,无弹性的细绳的一端分别固定在处,同质量的细绳下端系着一个称盘,且使得,试分析三根绳子受力的大小,判断哪根绳受力最大?
题后反思:(1)本题你还最想知道什么?
(2)绳子OB与绳子OC所受力的大小比较的本质是什么?
(3)你还能提出一些什么问题?
例2 已知: ,求证:.
题后反思:(1)你能否画出一个几何图形来解释例2?
(2)从例2中你能得出什么结论?
学生讨论得出结论:三角形ABC的三条高交于一点.
例3 已知直线经过点,用向量方法求的方程.
分析:设是直线上任意一点,由与共线的条件可推导得直线方程.
2.练习.
(1)已知作用于点的力的大小分别为6,8,且两力间的夹角为,则两力合力的大小为__ .
(2)在四边形中,·=0,=,则四边形是____ ___(直角梯形、菱形、矩形、正方形).
(3)如图,一个三角形角铁支架ABC安装在墙壁上,
AB∶AC∶BC=3∶4∶5,在B处挂一个6kg的物体,
求角铁AB与BC所受的力(取g=10m/s2).
(4)已知两点,,试用向量的方法证明以
线段为直径的圆的方程为.
(5)一条河两岸平行,河宽,一艘船从处出发航行到河的正对岸的处,船航行速度,水速,要使船垂直到达对岸所用的时间最少,与的夹角是多少?
五、要点归纳与方法小结
本节课学习了以下内容:
1.如何把物理学问题转化为数学问
2.如何把几何学问题转化为向量问题?
3.如何运用向量的平行四边形法则和力的平衡知识,作好力的分解和合成.
4.通过本节课的学习,让学生体会应用向量知识处理平面几何问题、力学问题与其它一些实际问题是一种行之有效的工具
5.数形结合法.
120o
10N
120o
10N
O
A
B
C
120o
10N
O
A
B
C
120o
O
A
B
C
D
A
O
B
C
(1)
A1
O
B1
(2)
C1
A
B
C
教学目标:
1.经历用向量方法解决某些简单的几何问题、力学问题的过程,体会向量是一种数学工具,发展学生运算能力和解决实际问题的能力;
2.运用向量的有关知识对物理中的问题进行相关分析和计算,并在这个过程中培养学生探究问题和解决问题的能力.
教学重点:
运用向量的有关知识对物理中的问题进行相关分析和计算,用向量方法解决实际问题的基本方法;向量法解决几何问题的“三步曲”.
教学难点:
实际问题转化为向量问题,体现向量的工具作 ( http: / / www.21cnjy.com )用.用向量的方法解决某些简单的平面几何问题、力学问题与其它一些实际问题,体会向量在几何、物理中的应用.
教学方法:
启发式教学.
教学过程:
一、情景创设
问题1 如图,用两条成120°角的等长的绳子悬挂
一个重量是10N的灯具,则每根绳子的拉力是多少?
二、学生活动
问题2 我们在图中标上相应的字母(如图),根据力的平衡理论,①绳子OA与绳子OB的拉力与灯具的重力G具有什么关系?
②绳子OA与绳子OB的拉力有什么关系?
学生讨论得出结论:①F1+F2+G=0.
②F1=F2.
问题3 如果将绳子OA的拉力表示为向量,绳子OB的拉力表示为向量,重力表示为向量,则向量、、之间有什么关系?
学生讨论得出结论:++=.这样物理问题就与数学中的向量产生了联系
三、建构数学
问题4 你能否根据以上信息,将这个物理问题编写成一个数学问题?你能解决这个问题吗?
学生讨论,教师整理,形成数学问题:已知向量、之间的夹角为120o,且向量的模等于向量的模,向量的模为10,求向量、的模.
学生讨论解决问题:
过A,B两点分别作OB、OA的平行线,相交于D点,则四边形OADB是菱形,连接OD,则OD=||=10,因为OA=OB=AD=BD,且∠AOB=120o,所以ΔOAD是等边三角形,
所以OA=AD=OD=10,即||=10,||=10.亦即每根绳子的拉力都是10N.
变题:在汽车站或火车站我们常见:两个人共提一个旅行包,若包重20N,还需什么条件,你能求每一个人手臂的拉力?
小结:(由学生讨论,教师整理)1.利用向量 ( http: / / www.21cnjy.com )解决物理问题的基本步骤:①问题转化,即把物理问题转化为数学问题;②建立模型,即建立以向量为载体的数学模型;③求解参数,即求向量的模、夹角、数量积等;④回答问题,即把所得的数学结论回归到物理问题.
2.用向量知识解决物理问题时,要注意数形结合.一般先要作出向量示意图,必要时可建立直角坐标系,再通过解三角形或坐标运算,求有关量的值.
四、数学应用
1.例题.
例1 如图(1)所示,无弹性的细绳的一端分别固定在处,同质量的细绳下端系着一个称盘,且使得,试分析三根绳子受力的大小,判断哪根绳受力最大?
题后反思:(1)本题你还最想知道什么?
(2)绳子OB与绳子OC所受力的大小比较的本质是什么?
(3)你还能提出一些什么问题?
例2 已知: ,求证:.
题后反思:(1)你能否画出一个几何图形来解释例2?
(2)从例2中你能得出什么结论?
学生讨论得出结论:三角形ABC的三条高交于一点.
例3 已知直线经过点,用向量方法求的方程.
分析:设是直线上任意一点,由与共线的条件可推导得直线方程.
2.练习.
(1)已知作用于点的力的大小分别为6,8,且两力间的夹角为,则两力合力的大小为__ .
(2)在四边形中,·=0,=,则四边形是____ ___(直角梯形、菱形、矩形、正方形).
(3)如图,一个三角形角铁支架ABC安装在墙壁上,
AB∶AC∶BC=3∶4∶5,在B处挂一个6kg的物体,
求角铁AB与BC所受的力(取g=10m/s2).
(4)已知两点,,试用向量的方法证明以
线段为直径的圆的方程为.
(5)一条河两岸平行,河宽,一艘船从处出发航行到河的正对岸的处,船航行速度,水速,要使船垂直到达对岸所用的时间最少,与的夹角是多少?
五、要点归纳与方法小结
本节课学习了以下内容:
1.如何把物理学问题转化为数学问
2.如何把几何学问题转化为向量问题?
3.如何运用向量的平行四边形法则和力的平衡知识,作好力的分解和合成.
4.通过本节课的学习,让学生体会应用向量知识处理平面几何问题、力学问题与其它一些实际问题是一种行之有效的工具
5.数形结合法.
120o
10N
120o
10N
O
A
B
C
120o
10N
O
A
B
C
120o
O
A
B
C
D
A
O
B
C
(1)
A1
O
B1
(2)
C1
A
B
C
