正方形性质判定
图片预览




文档简介
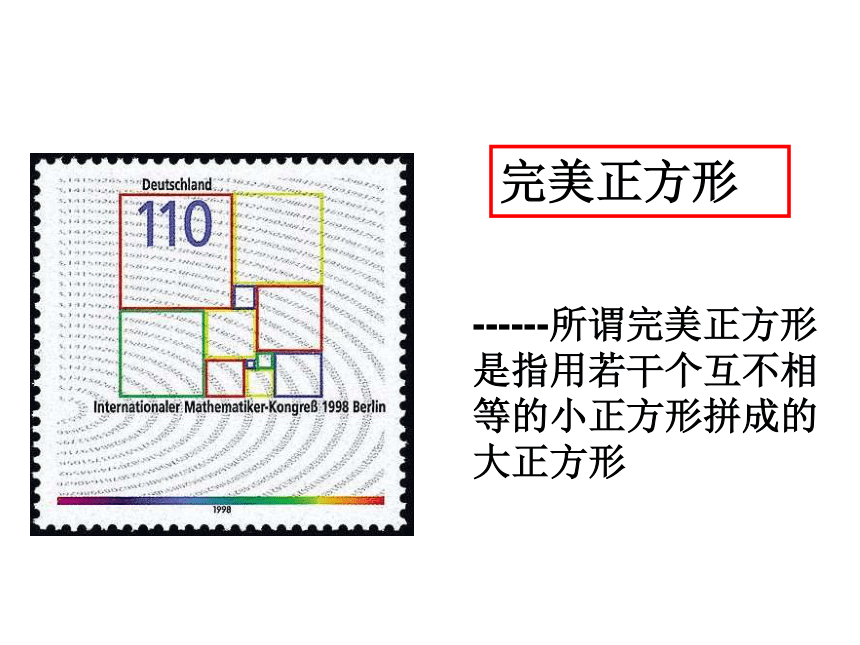
课件47张PPT。19.2.3 正方形特殊的平行四边形特殊的矩形特殊的菱形七巧板勾股定理完美正方形------所谓完美正方形
是指用若干个互不相
等的小正方形拼成的
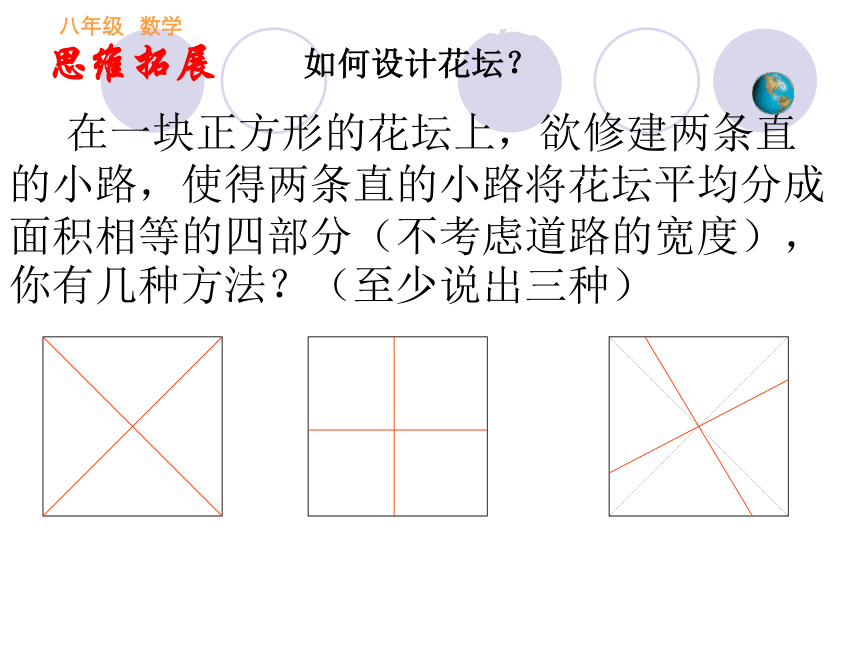
大正方形观察旋转 在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
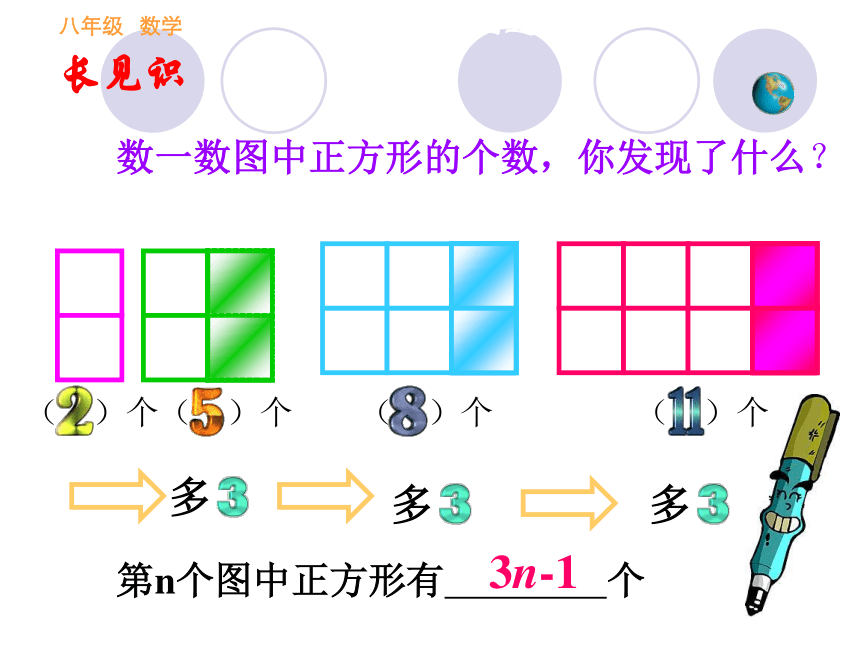
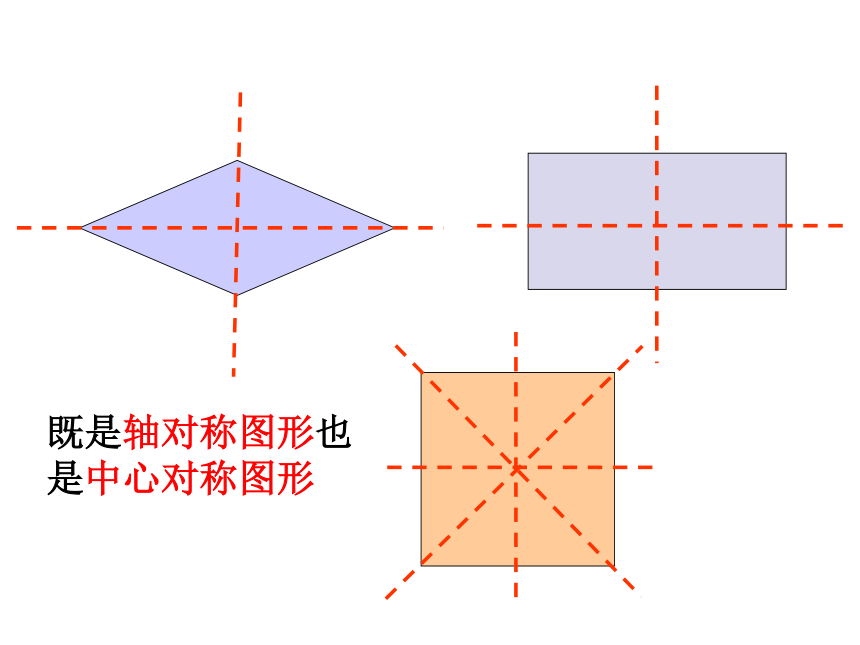
思维拓展如何设计花坛?八年级 数学第十九章 四边形数一数图中正方形的个数,你发现了什么? ( )个( )个 ( )个 ( )个第n个图中正方形有 个3n-1长见识八年级 数学第十九章 四边形既是轴对称图形也
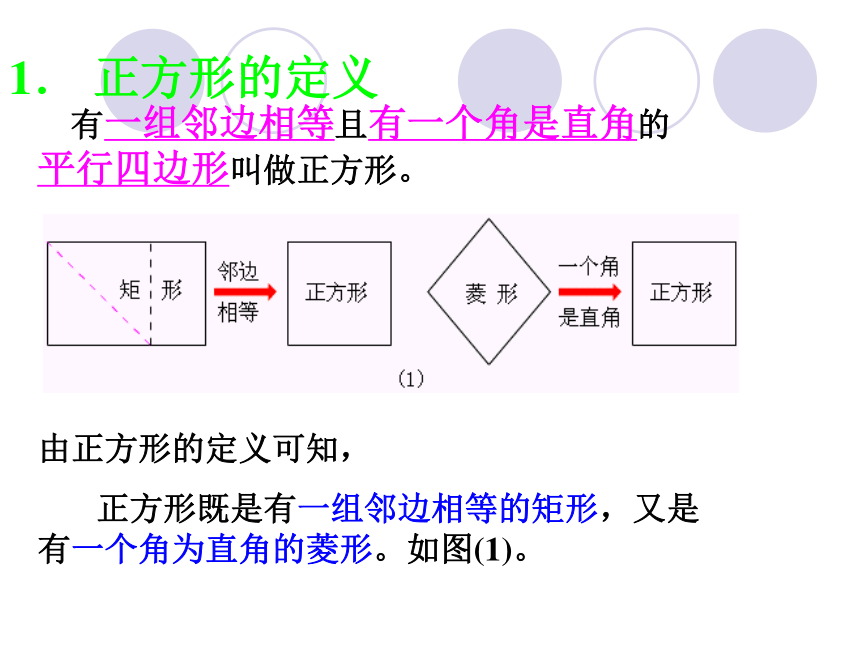
是中心对称图形1. 正方形的定义 由正方形的定义可知,
正方形既是有一组邻边相等的矩形,又是 有一个角为直角的菱形。如图(1)。 有一组邻边相等且有一个角是直角的平行四边形叫做正方形。
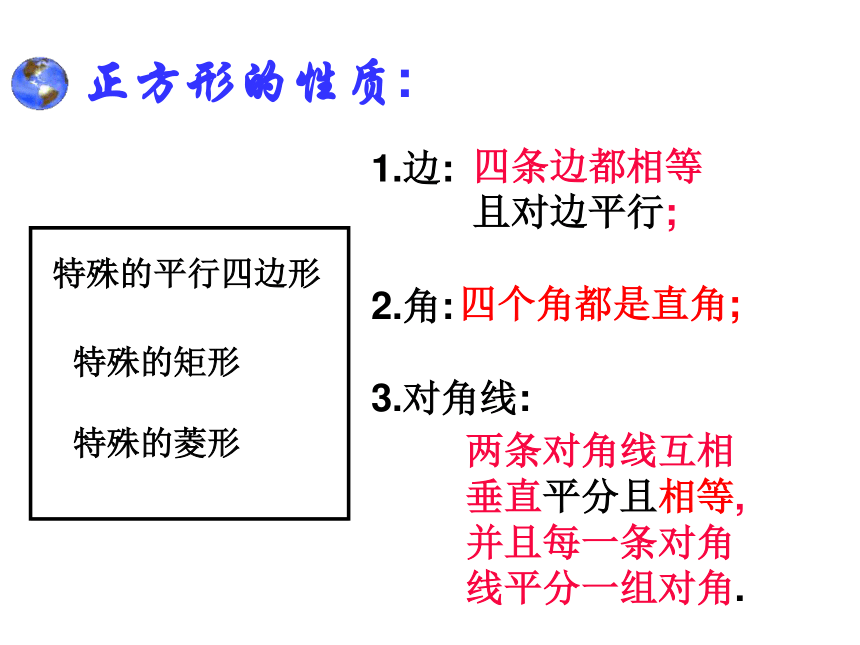
小结: 正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。?正方形的性质=特殊的平行四边形特殊的矩形特殊的菱形1.边:
2.角:
3.对角线:四条边都相等
且对边平行;两条对角线互相
垂直平分且相等,
并且每一条对角
线平分一组对角.四个角都是直角; 平行四边形矩形菱形正
方
形请画出平行四边形、矩形、菱形、正方形的关系图矩形菱形(2)
(3)(1)
(4)平行四边形正方形(1) AB=AD; (2) AC=BD;
(3) ∠BAD=90; (4) AC⊥BD。根据图形所具有的性质,在下表相应的空格中打 ”√”√√√√√√√√√√√√√√√√已知:如图正方形ABCD对角线AC、BD 相交于O点.求证: △ABO 、 △BCO 、 △CDO 、△ADO是全等的等腰直角三角形. 求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形。ABCDO范例:2、周长为20cm的正方形,边长是 对角线长是 面积是 。自我检测3、正方形两条对角线的和为8cm,它的面积为____________. 1、选择题 下列判断中正确的是( )
A、四边相等的四边形是正方形
B、四角相等的四边形是正方形 C、对角线垂直的平行四边形是正方形
D、对角线互相垂直平分且相等的四边形是正方形
4、正方形具有而矩形不一定有的性质是( )
A.四个角是直角 B.对角线互相垂直
C.对角线互相平分 D.对角线相等
5.矩形,菱形,正方形都具有的性质是( )
A.邻边相等 B. 邻角相等
C.对边相等 D. 对角互补活动1.从长方形木板中怎样截出最大的正方形木板?2.怎样使菱形的衣帽架变成正方形的衣帽架?3.昨天,我去超市买了一条方巾,现在想请同学们帮助检验
一下方巾是否是正方形的。有一个角是直角有一组邻边相等有一组邻边相等有一个角是直角有一组邻边相等且有一个角是直角正方形、矩形、菱形及平行四边形四者之间的关系三、正方形的判定1、 有一组邻边相等并且有一个角是直角的平行四边形是正方形。2、 有一组邻边相等的矩形是正方形或者
有一个角是直角的菱形是正方形。 定义法:矩形菱形法: 对角线法:3、 两条对角线互相垂直且相等的平行四边形是正方形。你能总结出正方形有哪些判定方法吗?满足下列条件的四边形是不是正方形:
(1)对角线互相垂直且相等的平行四边形;
(2)对角线互相垂直的矩形;
(3)对角线相等的菱形;
(4)对角线互相垂直平分且相等的四边形.练一练:既是矩形又是菱形 ——— 正方形判定正方形要准备的条件:平行四边形、一组邻边相等、一个角是直角 练习:求证:对角线垂直平分且相等的四边形是正方形。 已知:如图(3),四边形ABCD中对角线
AC、BD相交于点O,且AC=BD,
AO=CO,BO=DO,AC⊥BD。
求证:四边形ABCD是正方形。 请大家先根据题意,画出图形然后写出已知,求证,求证:对角线垂直平分且相等的四边形是正方形。 已知:如图(3),四边形ABCD中对角线
证明:
∵AO=CO,BO=DO ∴四边形ABCD是平行四边形
又AC=BD ∴平行四边形ABCD是矩形 又∵AC⊥BD ∴平行四边形ABCD是菱形,即四边形ABCD是正方形 解题小结: 正方形即是特殊的矩形,又是特殊的菱形。它没有明确的判定定理,要判定一个四边形是正方形,基本思路就是证明这个四边形既是菱形又是矩形。因而得到这个四边形是正方形。事实上,我们可以把本例作为正方形的一个判定定理:即:即角线垂直平分且相等的四边形是正方形。 AC、BD相交于点O,且AC=BD,AO=CO, BO=DO,AC⊥BD。 求证:四边形ABCD是正方形。
把一个长方形纸片如图那样折一下,就可以裁出正方形纸片,为什么?如果是一个长方形木板,又如何从中裁出
一个最大的正方形木板呢?实际问题:已知:∠DAB=∠B=∠ADC
=90°,AB=AD.求证:四边形ABCD是正方形取AD=AB,BC=AB即可.判断对错1. 四边相等的四边形是正方形
2.四角相等的四边形是正方形
3.对角线垂直的平行四边形是正方形
4.四条边相等且有一个角是直角的四边形是正方形练习:在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F.
1)试说明:DE=DF
2)只添加一个条件,使四边形EDFA是正方形.
请你至少写出两种不同的添加方法.(不另外
添加辅助线)范例精讲 例1:已知:如图(2),点A‘、B’、C‘、D’分别是正方形ABCD
的边AB、BC、CD、DA的中点,
求证:四边形A'B'C'D'是正方形。 分析(1)你能证明四边形是矩形吗?
(2)你能证明四边形是菱形吗??
(3)你能证明四边形是正方形吗?? 请大家完成证明证明:
∵四边形ABCD是正方形 ∴AD=AB=BC, ∠A=∠B=90° 又∵AD‘=AD AA’=A‘B=AB BB’=BC ∴AD’=AA’=A‘B=BB’ ∴∠1=∠2=∠3=∠4=45°
∴∠D‘A’B‘=180°-∠1-∠3=180°-45°-45°=90° 同理:∠A’B‘C’=90° ∠B‘C’D‘=90° ∴四边形A’B‘C’D‘是矩形
在△D’AA‘和△A’BB‘中
∴△D'AA'≌△A'BB'(SAS) ∴A'D'=A'B' ∴四边形A'B'C'D'是正方形(有一组邻边相等的矩形是正方形) 学习如逆水行舟不进则退应用举例:已知:如图点A' 、 B' 、 C'、D'分别是正方形ABCD
四条边上的点,并且AA'=BB'=CC'=DD'
求证:四边形A'B'C'D'是正方形①、由已知正方形证三角形全等;
②、证得菱形;
③、再证直角;
④、是正方形证题思路分析练习:正方形ABCD中,对角线AC和BD交于点O,点A`,B`,C`,D`分别是AO,BO,CO,DO的中点,判断四边形A`B`C`D`的形状。说明原因ABCDD`C`B`A`O正方形ABCD中,对角线AC和BD交于点O,点A`,B`,C`,D`分别在AC、BD上, 且AA`=BB`=CC`=DD`. 判断四边形A`B`C`D`的形状 ABDD`C`B`A`OC练习:矩形ABCD中,四个内角的平分线组成四边形EMFN, 判断四边形EMFN的形状,并说明原因ABCDNFME例2.已知:如图(4)矩形ABCD中,∠A、∠B、∠C、∠D 的平分线组成四边形A'B'C'D',
分析:
判定一个四边形是正方形可以选择:
求证:四边形A'B'C'D'是正方形。下面请大家进行证明。 (1)先证明它是矩形,再证它有一组邻 边相等; (2)先证明它是菱形,再证它有一个角等于90°已知:如图(4)矩形ABCD中,∠A、∠B、∠C、∠D的 平分线组成四边形A'B'C'D',
证明:在四边形ABCD中
求证:四边形A'B'C'D'是正方形。 又∵AB‘=BD’ 且AA‘=BA’(已证) AB'-AA'=BD'-BA' A'B'=A'D' ∴四边形A'B'C'D'是正方形(有一组邻边相等的矩形是正方形)
∵AB'、BD'、CD'、DB'分别平分∠DAB、∠ABC、∠BCD、∠CDA ∴∠B'=∠D'=90°∴∠1=∠2=∠3=∠4=45° AD=BC ∴△AB'D≌△BD'C (ASA) ∴AB'=BD'=CD'=DB' 同理可证:∠D'A'B'=∠D'C'B'=90且AA'=BA'=CC'=DC' ∴四边形A'B'C'D'是矩形(有三个角都是直角的四边形是矩形) 1:在Rt△ABC中∠C=90,∠A,∠B的平分线相交于点D,DF⊥BC交BC于点F,DE⊥AC交AC于点E。
求证:四边形CEDF是正方形
FDCBEA巩固练习:如图,四边形ABCD和AEFG都是正方形, 求证:BE = DG
ABCD是一块正方形场地,小华和小芳在AB
边上取定了一点E,经测量知 EC=30m,
EB=10m,这块场地的面积和对角线长分别
是多少(对角线长精确到0.1m)?练一练:ABCDE1、正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F
求证:(1)OE = OF EABCDOGF综合运用:(2)若E是OB的延长线上的一点,OE = OF还成立吗? EABCDOGF 例2如图(3),正方形ABCD中,AC、BD相交于O,
分析:要证明BM=CN,大家观察
图形可以考虑证哪两个三角形全等 ?
MN∥AB且MN分别交OA、OB于M、N。求证:BM=CN。
你能完成证明吗???
AB=BC,∠1=∠2=45 ° 条件够吗? 还需要的条件是 AM=BN
△ABM≌△BCN
你所要证明的两个三角形已经满足
了哪些条件?
由正方形可以得到的条件有: 例2.如图(3),正方形ABCD中,AC、BD相交于O,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。 证明:
∵四边形ABCD是正方形 ∴OA=OB ,
∠1=∠2=∠3=45° 又∵MN∥AB
∴∠OMN=∠1=∠3=∠ONM=45° ∴OM=ON ∴OA-OM=OB-ON 即AM=BN 下面大家自己完成证明 练习1.
已知:正方形ABCD对角线AC、BD相 交于点O,且AB=acm,如图(2)。
求:AC的长及正方形的面积S。 练习2.
已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6 cm,如图
求:正方形的面积S。
例3.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45° 分析:
欲证∠MFD=45°,只要
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____要证MD=FD,大家只须证得哪两个三角形全等?
试一试
看能不能完成证明???△CMD≌△ADFDMDF例3.已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M, 求证:∠MFD=45° 证明:
∵CE⊥AF ∴∠ADC=∠AEM=90° 又∵∠CMD=∠AME ∴∠1=∠2 又∵CD=AD,∠ADF=∠MDC ∴Rt△CDM≌Rt△ADF (AAS) ∴DM=DF
下面的证明请大家完成
练习.如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB
(2) BH⊥AF
证明:
例4.如图(6),△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。 求证:∠CEA=∠ABG 分析:欲证∠CEA=∠ABG,
大家想一想证明两个角相等的方法,
你有办法了吗???通过自己的努力,看能不能解决问题?
证明:∵四边形ABDE和四边形ACFG是正方形。 ∴AE=AB AG=AC ∠1=∠2=90° 又∵∠EAC=∠1+∠BAC=90°+∠BAC ∠BAG=∠2+∠BAC=90°+∠BAC ∴∠EAC=∠BAG ∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG 小结:特殊的平行四边形、特殊的矩形、特殊的菱形一、什么是正方形:既是矩形又是菱形 ——— 正方形二、正方形有什么性质:具有矩形、菱形、平行四边形的所有性质
是指用若干个互不相
等的小正方形拼成的
大正方形观察旋转 在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
思维拓展如何设计花坛?八年级 数学第十九章 四边形数一数图中正方形的个数,你发现了什么? ( )个( )个 ( )个 ( )个第n个图中正方形有 个3n-1长见识八年级 数学第十九章 四边形既是轴对称图形也
是中心对称图形1. 正方形的定义 由正方形的定义可知,
正方形既是有一组邻边相等的矩形,又是 有一个角为直角的菱形。如图(1)。 有一组邻边相等且有一个角是直角的平行四边形叫做正方形。
小结: 正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。?正方形的性质=特殊的平行四边形特殊的矩形特殊的菱形1.边:
2.角:
3.对角线:四条边都相等
且对边平行;两条对角线互相
垂直平分且相等,
并且每一条对角
线平分一组对角.四个角都是直角; 平行四边形矩形菱形正
方
形请画出平行四边形、矩形、菱形、正方形的关系图矩形菱形(2)
(3)(1)
(4)平行四边形正方形(1) AB=AD; (2) AC=BD;
(3) ∠BAD=90; (4) AC⊥BD。根据图形所具有的性质,在下表相应的空格中打 ”√”√√√√√√√√√√√√√√√√已知:如图正方形ABCD对角线AC、BD 相交于O点.求证: △ABO 、 △BCO 、 △CDO 、△ADO是全等的等腰直角三角形. 求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形。ABCDO范例:2、周长为20cm的正方形,边长是 对角线长是 面积是 。自我检测3、正方形两条对角线的和为8cm,它的面积为____________. 1、选择题 下列判断中正确的是( )
A、四边相等的四边形是正方形
B、四角相等的四边形是正方形 C、对角线垂直的平行四边形是正方形
D、对角线互相垂直平分且相等的四边形是正方形
4、正方形具有而矩形不一定有的性质是( )
A.四个角是直角 B.对角线互相垂直
C.对角线互相平分 D.对角线相等
5.矩形,菱形,正方形都具有的性质是( )
A.邻边相等 B. 邻角相等
C.对边相等 D. 对角互补活动1.从长方形木板中怎样截出最大的正方形木板?2.怎样使菱形的衣帽架变成正方形的衣帽架?3.昨天,我去超市买了一条方巾,现在想请同学们帮助检验
一下方巾是否是正方形的。有一个角是直角有一组邻边相等有一组邻边相等有一个角是直角有一组邻边相等且有一个角是直角正方形、矩形、菱形及平行四边形四者之间的关系三、正方形的判定1、 有一组邻边相等并且有一个角是直角的平行四边形是正方形。2、 有一组邻边相等的矩形是正方形或者
有一个角是直角的菱形是正方形。 定义法:矩形菱形法: 对角线法:3、 两条对角线互相垂直且相等的平行四边形是正方形。你能总结出正方形有哪些判定方法吗?满足下列条件的四边形是不是正方形:
(1)对角线互相垂直且相等的平行四边形;
(2)对角线互相垂直的矩形;
(3)对角线相等的菱形;
(4)对角线互相垂直平分且相等的四边形.练一练:既是矩形又是菱形 ——— 正方形判定正方形要准备的条件:平行四边形、一组邻边相等、一个角是直角 练习:求证:对角线垂直平分且相等的四边形是正方形。 已知:如图(3),四边形ABCD中对角线
AC、BD相交于点O,且AC=BD,
AO=CO,BO=DO,AC⊥BD。
求证:四边形ABCD是正方形。 请大家先根据题意,画出图形然后写出已知,求证,求证:对角线垂直平分且相等的四边形是正方形。 已知:如图(3),四边形ABCD中对角线
证明:
∵AO=CO,BO=DO ∴四边形ABCD是平行四边形
又AC=BD ∴平行四边形ABCD是矩形 又∵AC⊥BD ∴平行四边形ABCD是菱形,即四边形ABCD是正方形 解题小结: 正方形即是特殊的矩形,又是特殊的菱形。它没有明确的判定定理,要判定一个四边形是正方形,基本思路就是证明这个四边形既是菱形又是矩形。因而得到这个四边形是正方形。事实上,我们可以把本例作为正方形的一个判定定理:即:即角线垂直平分且相等的四边形是正方形。 AC、BD相交于点O,且AC=BD,AO=CO, BO=DO,AC⊥BD。 求证:四边形ABCD是正方形。
把一个长方形纸片如图那样折一下,就可以裁出正方形纸片,为什么?如果是一个长方形木板,又如何从中裁出
一个最大的正方形木板呢?实际问题:已知:∠DAB=∠B=∠ADC
=90°,AB=AD.求证:四边形ABCD是正方形取AD=AB,BC=AB即可.判断对错1. 四边相等的四边形是正方形
2.四角相等的四边形是正方形
3.对角线垂直的平行四边形是正方形
4.四条边相等且有一个角是直角的四边形是正方形练习:在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F.
1)试说明:DE=DF
2)只添加一个条件,使四边形EDFA是正方形.
请你至少写出两种不同的添加方法.(不另外
添加辅助线)范例精讲 例1:已知:如图(2),点A‘、B’、C‘、D’分别是正方形ABCD
的边AB、BC、CD、DA的中点,
求证:四边形A'B'C'D'是正方形。 分析(1)你能证明四边形是矩形吗?
(2)你能证明四边形是菱形吗??
(3)你能证明四边形是正方形吗?? 请大家完成证明证明:
∵四边形ABCD是正方形 ∴AD=AB=BC, ∠A=∠B=90° 又∵AD‘=AD AA’=A‘B=AB BB’=BC ∴AD’=AA’=A‘B=BB’ ∴∠1=∠2=∠3=∠4=45°
∴∠D‘A’B‘=180°-∠1-∠3=180°-45°-45°=90° 同理:∠A’B‘C’=90° ∠B‘C’D‘=90° ∴四边形A’B‘C’D‘是矩形
在△D’AA‘和△A’BB‘中
∴△D'AA'≌△A'BB'(SAS) ∴A'D'=A'B' ∴四边形A'B'C'D'是正方形(有一组邻边相等的矩形是正方形) 学习如逆水行舟不进则退应用举例:已知:如图点A' 、 B' 、 C'、D'分别是正方形ABCD
四条边上的点,并且AA'=BB'=CC'=DD'
求证:四边形A'B'C'D'是正方形①、由已知正方形证三角形全等;
②、证得菱形;
③、再证直角;
④、是正方形证题思路分析练习:正方形ABCD中,对角线AC和BD交于点O,点A`,B`,C`,D`分别是AO,BO,CO,DO的中点,判断四边形A`B`C`D`的形状。说明原因ABCDD`C`B`A`O正方形ABCD中,对角线AC和BD交于点O,点A`,B`,C`,D`分别在AC、BD上, 且AA`=BB`=CC`=DD`. 判断四边形A`B`C`D`的形状 ABDD`C`B`A`OC练习:矩形ABCD中,四个内角的平分线组成四边形EMFN, 判断四边形EMFN的形状,并说明原因ABCDNFME例2.已知:如图(4)矩形ABCD中,∠A、∠B、∠C、∠D 的平分线组成四边形A'B'C'D',
分析:
判定一个四边形是正方形可以选择:
求证:四边形A'B'C'D'是正方形。下面请大家进行证明。 (1)先证明它是矩形,再证它有一组邻 边相等; (2)先证明它是菱形,再证它有一个角等于90°已知:如图(4)矩形ABCD中,∠A、∠B、∠C、∠D的 平分线组成四边形A'B'C'D',
证明:在四边形ABCD中
求证:四边形A'B'C'D'是正方形。 又∵AB‘=BD’ 且AA‘=BA’(已证) AB'-AA'=BD'-BA' A'B'=A'D' ∴四边形A'B'C'D'是正方形(有一组邻边相等的矩形是正方形)
∵AB'、BD'、CD'、DB'分别平分∠DAB、∠ABC、∠BCD、∠CDA ∴∠B'=∠D'=90°∴∠1=∠2=∠3=∠4=45° AD=BC ∴△AB'D≌△BD'C (ASA) ∴AB'=BD'=CD'=DB' 同理可证:∠D'A'B'=∠D'C'B'=90且AA'=BA'=CC'=DC' ∴四边形A'B'C'D'是矩形(有三个角都是直角的四边形是矩形) 1:在Rt△ABC中∠C=90,∠A,∠B的平分线相交于点D,DF⊥BC交BC于点F,DE⊥AC交AC于点E。
求证:四边形CEDF是正方形
FDCBEA巩固练习:如图,四边形ABCD和AEFG都是正方形, 求证:BE = DG
ABCD是一块正方形场地,小华和小芳在AB
边上取定了一点E,经测量知 EC=30m,
EB=10m,这块场地的面积和对角线长分别
是多少(对角线长精确到0.1m)?练一练:ABCDE1、正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F
求证:(1)OE = OF EABCDOGF综合运用:(2)若E是OB的延长线上的一点,OE = OF还成立吗? EABCDOGF 例2如图(3),正方形ABCD中,AC、BD相交于O,
分析:要证明BM=CN,大家观察
图形可以考虑证哪两个三角形全等 ?
MN∥AB且MN分别交OA、OB于M、N。求证:BM=CN。
你能完成证明吗???
AB=BC,∠1=∠2=45 ° 条件够吗? 还需要的条件是 AM=BN
△ABM≌△BCN
你所要证明的两个三角形已经满足
了哪些条件?
由正方形可以得到的条件有: 例2.如图(3),正方形ABCD中,AC、BD相交于O,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。 证明:
∵四边形ABCD是正方形 ∴OA=OB ,
∠1=∠2=∠3=45° 又∵MN∥AB
∴∠OMN=∠1=∠3=∠ONM=45° ∴OM=ON ∴OA-OM=OB-ON 即AM=BN 下面大家自己完成证明 练习1.
已知:正方形ABCD对角线AC、BD相 交于点O,且AB=acm,如图(2)。
求:AC的长及正方形的面积S。 练习2.
已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6 cm,如图
求:正方形的面积S。
例3.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45° 分析:
欲证∠MFD=45°,只要
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____要证MD=FD,大家只须证得哪两个三角形全等?
试一试
看能不能完成证明???△CMD≌△ADFDMDF例3.已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M, 求证:∠MFD=45° 证明:
∵CE⊥AF ∴∠ADC=∠AEM=90° 又∵∠CMD=∠AME ∴∠1=∠2 又∵CD=AD,∠ADF=∠MDC ∴Rt△CDM≌Rt△ADF (AAS) ∴DM=DF
下面的证明请大家完成
练习.如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB
(2) BH⊥AF
证明:
例4.如图(6),△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。 求证:∠CEA=∠ABG 分析:欲证∠CEA=∠ABG,
大家想一想证明两个角相等的方法,
你有办法了吗???通过自己的努力,看能不能解决问题?
证明:∵四边形ABDE和四边形ACFG是正方形。 ∴AE=AB AG=AC ∠1=∠2=90° 又∵∠EAC=∠1+∠BAC=90°+∠BAC ∠BAG=∠2+∠BAC=90°+∠BAC ∴∠EAC=∠BAG ∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG 小结:特殊的平行四边形、特殊的矩形、特殊的菱形一、什么是正方形:既是矩形又是菱形 ——— 正方形二、正方形有什么性质:具有矩形、菱形、平行四边形的所有性质
