人教版八年级数学下册第十七章 勾股定理 单元复习题 (含答案)
文档属性
| 名称 | 人教版八年级数学下册第十七章 勾股定理 单元复习题 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 268.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-20 00:00:00 | ||
图片预览


文档简介
第十七章 勾股定理 单元复习题 人教版八年级数学下册
一、选择题
1.如图,由六个边长为的小正方形构成一个大长方形,连接小正方形的三个顶点,可得到,则中边上的高是( )
A. B. C. D.
2.如图,长方形中,,,在数轴上,若以点为圆心,的长为半径作弧交数轴于点,则点表示的数为
A. B. C.2 D.
3. 小华新买了一条跳绳,如图1,他按照体育老师教的方法确定适合自己的绳长:一脚踩住绳子的中央,手肘靠近身体,两肘弯屈,小臂水平转向两侧,两手将绳拉直,绳长即合适长度。将图1抽象成如图2,若两手握住的绳柄两端距离约为1米,小臂到地面的距离约1. 2米,则适合小华的绳长为( )
A.2. 2米 B.2. 4米 C.2. 6米 D.2. 8米
4.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大的正方形内,若知道图中阴影部分的面积,则一定能求出( )
A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
5.以下列数据为长度的线段中,可以构成直角三角形的是( )
A.1,, B.,3,5 C.1,2,3 D.2,3,4
6.下列是勾股数的是
A.12,15,18 B.6,10,7 C.12,16,20 D.,,
7.下列各组数中不能作为直角三角形的三边长的是( )
A.2,3,4 B.3,4,5 C.5,12,13 D.7,24,25
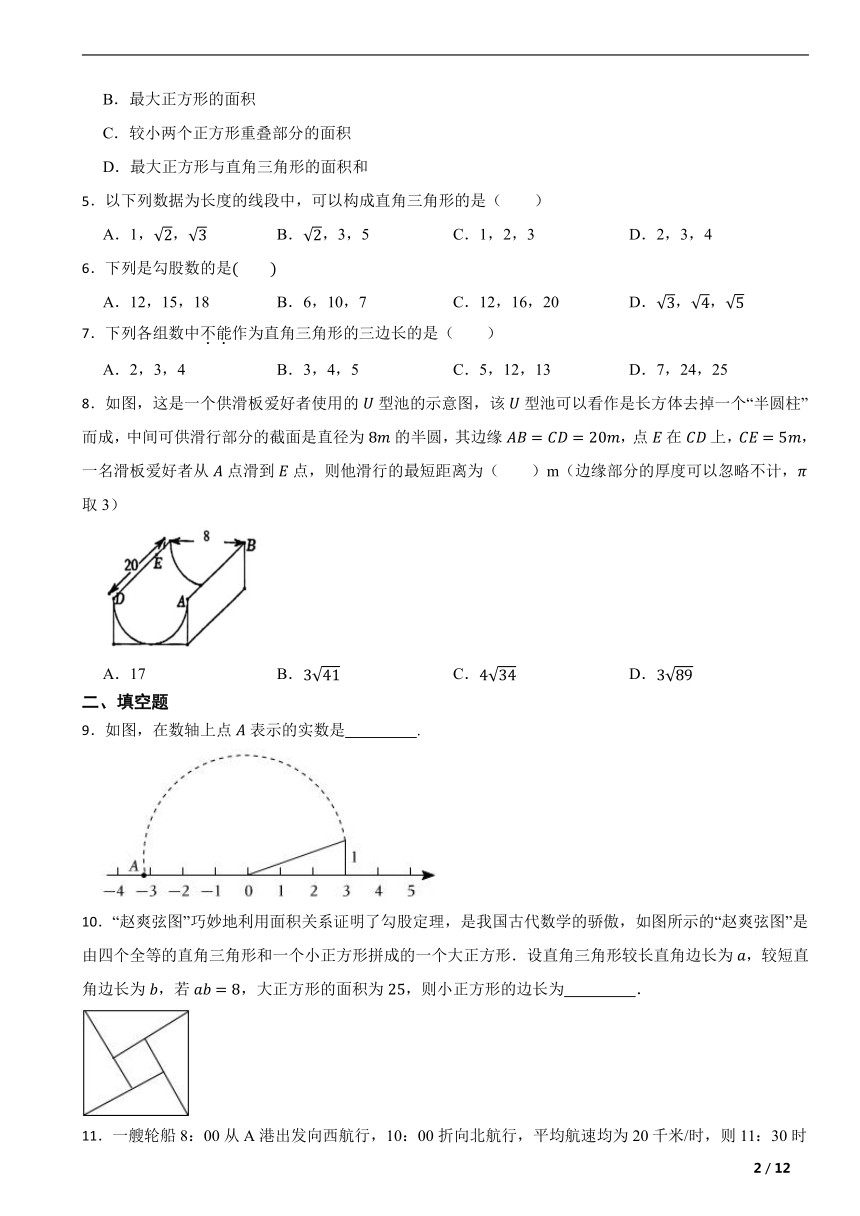
8.如图,这是一个供滑板爱好者使用的型池的示意图,该型池可以看作是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为的半圆,其边缘,点在上,,一名滑板爱好者从点滑到点,则他滑行的最短距离为( )m(边缘部分的厚度可以忽略不计,取3)
A.17 B. C. D.
二、填空题
9.如图,在数轴上点表示的实数是 .
10.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为,较短直角边长为,若,大正方形的面积为,则小正方形的边长为 .
11.一艘轮船8:00从A港出发向西航行,10:00折向北航行,平均航速均为20千米/时,则11:30时该轮船离A港的距离为 .
12.如图,将长为的弹性绳放置在直线上,固定端点和,然后把中点竖直向上拉升至点,则拉长后弹性绳的长为 .
13.如图,已知圆柱底面的周长为6dm,圆柱高为4dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为
14.《九章算术》中一道“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”题意是:有一个池塘,其水面是边长为10尺的正方形,一棵芦苇AC生长在它的中央,高出水面部分BC为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部C恰好碰到岸边的C'处(如图),求水深和芦苇长各多少尺?该问题中的水深为 尺.
三、解答题
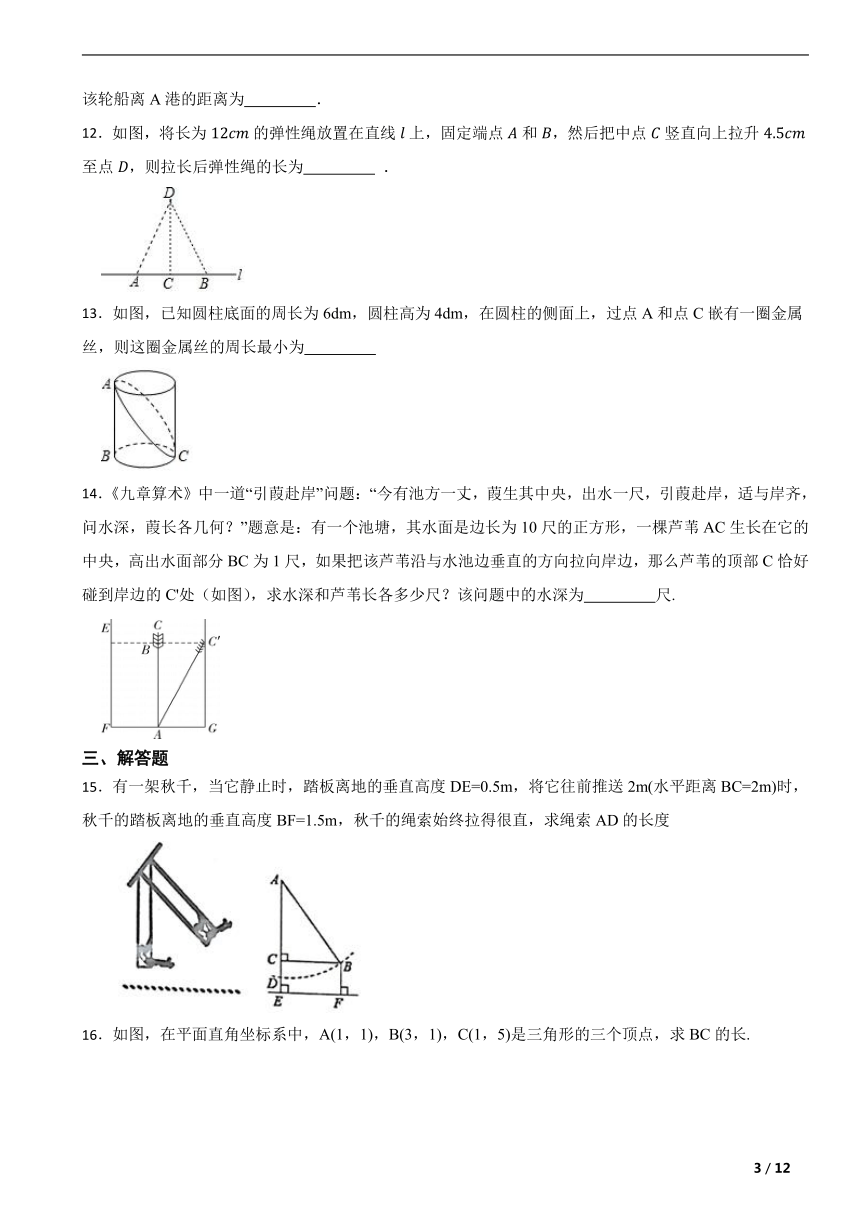
15.有一架秋千,当它静止时,踏板离地的垂直高度DE=0.5m,将它往前推送2m(水平距离BC=2m)时,秋千的踏板离地的垂直高度BF=1.5m,秋千的绳索始终拉得很直,求绳索AD的长度
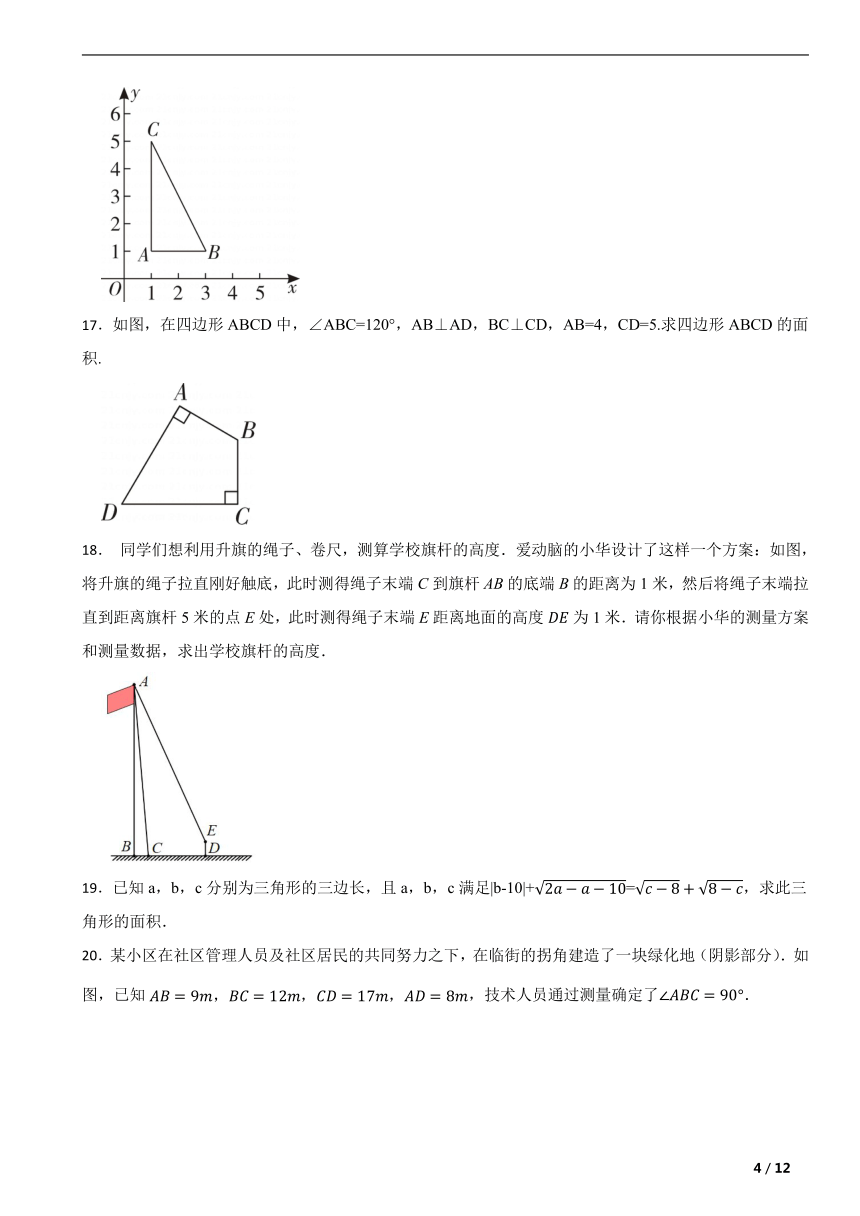
16.如图,在平面直角坐标系中,A(1,1),B(3,1),C(1,5)是三角形的三个顶点,求BC的长.
17.如图,在四边形ABCD中,∠ABC=120°,AB⊥AD,BC⊥CD,AB=4,CD=5.求四边形ABCD的面积.
18. 同学们想利用升旗的绳子、卷尺,测算学校旗杆的高度.爱动脑的小华设计了这样一个方案:如图,将升旗的绳子拉直刚好触底,此时测得绳子末端C到旗杆AB的底端B的距离为1米,然后将绳子末端拉直到距离旗杆5米的点E处,此时测得绳子末端E距离地面的高度为1米.请你根据小华的测量方案和测量数据,求出学校旗杆的高度.
19.已知a,b,c分别为三角形的三边长,且a,b,c满足|b-10|+=,求此三角形的面积.
20.某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角建造了一块绿化地(阴影部分).如图,已知,技术人员通过测量确定了.
(1)小区内部分居民每天必须从点经过点再到点位置,为了方便居民出人,技术人员打算在绿地中开辟一条从点直通点的小路,请问如果方案落实施工完成,居民从点到点将少走多少路程?
(2)这片绿地的面积是多少?
答案解析部分
1.【答案】A
【解析】【解答】解:设中边上的高为h,
由勾股定理,得,
∵,,
即,
解得:
故中边上的高是.
故答案为:A.
【分析】根据勾股定理求出,根据题意得出的面积等于正方形面积减去其他3个三角形的面积,再利用三角形等面积法求出三角形的高即可.
2.【答案】A
【解析】【解答】解:∵四边形ABCD是长方形,
∴∠B=90°,BC=AD=1,
∴,
∵ 以点A为圆心,AC的长为半径作弧交数轴于点M,
∴AM=AC=,
∵点A所表示的数为-1,
∴点M到原点的距离为,
又∵点M在原点的右边,
∴点M表示的数为.
故答案为:A.
【分析】由矩形的性质得∠B=90°,BC=AD=1,进而由勾股定理算出AC=,由同圆的半径相等得AM=AC=,然后找出点M到原点的距离,并结合点M在原点的右边即可得出点M所表示的数.
3.【答案】C
【解析】【解答】解:标字母如图所示,过C作CD⊥AB于点D.
由题意得:AC=BC,AB=1米,
∴AD=BD=0.5(米).
在Rt△BCD中,∴BD=1.2米,
∴BC=AC===1.3(米),
∴绳长为1.3×2=2.6(米).
故答案为:C.
【分析】由题意得出图形是等腰三角形,再根据等腰三角形“三线合一”的性质和勾股定理求解即可.
4.【答案】C
【解析】【解答】解:设直角三角形的各边长为a,b,c,满足a2+c2=c2,
可以得到:阴影部分面积+小正方形面积+大正方形面积-重叠部分面积=最大正方形面积,
即:阴影部分面积+a2+b2-重叠部分面积=c2.
所以有阴影部分面积=重叠部分面积.
故答案为:C.
【分析】结合勾股定理的几何意义,将三个正方形的面积联系起来,再用两种方法表示出最大正方形的面积,问题得到解决.
5.【答案】A
【解析】【解答】A:正确.
B:,错误.
C:
D:
故答案为A.
【分析】用勾股定理逆定理,关键是掌握如果三角形的三边长a,b,c满足,那么这个三角形就是直角三角形,
据此先求出两小边的平方和,再求出最长边的平方,最后看看是否相等即可.
6.【答案】C
【解析】【解答】解:A、∵122+152=144+225=369≠182=364,∴ 12,15,18不是一组勾股数,故此选项不符合题意;
B、∵62+72=36+49=85≠102=100,∴ 6,10,7不是一组勾股数,故此选项不符合题意;
C、∵122+162=144+256=400=202,∴ 12,16,20是一组勾股数,故此选项符合题意;
D、∵,, 不是一组正整数,∴不是一组勾股数,故此选项不符合题意.
故答案为:C.
【分析】能够构成一个直角三角形三边的三个正整数就是勾股数,据此逐项判断得出答案.
7.【答案】A
8.【答案】B
【解析】【解答】解:将半圆面展开可得:
米,米,
在中,由勾股定理得米,
即滑行的最短距离为米,
故答案为:B.
【分析】将半圆面展开可得,、、三点构成直角三角形,为斜边,为半圆的长,,根据勾股定理计算求解即可.
9.【答案】
【解析】【解答】解:由图形得OB==,
∴OA=OB=,
∴ 在数轴上点表示的实数是- .
故答案为:-.
【分析】由勾股定理求出OB=,即得OA=OB=,继而得解.
10.【答案】3
【解析】【解答】解:由题意知:中间小正方形的边长为:a -b
∵每一个直角三角形的面积为:ab=x8=4
∴4xab+(a-b)2=25
∴(a-b)2=25-16=9
∴a-b=3或a-b=-3(舍去)
故答案为:3.
【分析】本题主要考查勾股定理,熟练运用勾股定理及完全平方公式是解题的关键.
11.【答案】50千米
12.【答案】
【解析】【解答】解:∵占C是AB的中点,
∴AC=CB=6cm,
在中,(cm)
∴拉长后弹性绳的长为 :AD+BD=2AD=15cm。
故答案为:15cm。
【分析】根据勾股定理计算即可。
13.【答案】10dm
【解析】【解答】解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.
∵圆柱底面的周长为6dm,圆柱高为4dm,
∴AB=4dm,BC=BC′=3dm,
∴AC2=42+32=25,
∴AC=5dm,
∴这圈金属丝的周长最小为2AC=10dm.
故答案为:10dm
【分析】要求丝线的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,根据勾股定理计算即可.
14.【答案】12
【解析】【解答】解:依题意画出图形,
设芦苇长AC=AC′=x尺,
则水深AB=(x﹣1)尺,
∵C′E=10尺,
∴C′B=5尺,
在Rt△AC′B中,
52+(x﹣1)2=x2,
解得:x=13,
即芦苇长13尺,水深为12尺,
故答案为:12.
【分析】首先把事物图抽象数学几何图形,由图根据题意,可知EC′的长为10尺,从而求得C′B=5尺,然后设芦苇长AC=AC′=x尺,则水深AB为(x﹣1)尺,根据勾股定理列出方程,求解即可得到芦苇的长和水深.
15.【答案】解:在Rt△ACB中,AC2+BC2=AB2,
设秋千的绳索长为xm,则AC=(x﹣1)m,
故x2=22+(x﹣1)2,
解得:x=2.5,
答:绳索AD的长度是2.5m.
【解析】【分析】 设秋千的绳索长为xm,得出AC=(x﹣1)m, 利用勾股定理得出AC2+BC2=AB2, 从而得出关于x的方程,解方程求出x的值,即可得出答案.
16.【答案】解:∵A(1,1),B(3,1),C(1,5),
∴AC=5-1=4,AB=3-1=2,
在Rt△ABC中,
.
【解析】【分析】根据点A、B、C的坐标求出AB、AC的长度,再利用直角三角形中,两条直角边长的平方之和一定等于斜边长的平方列式计算即可求解.
17.【答案】9
18.【答案】解:12.5米
【解析】【解答】过点E作EF⊥AB于F,如图所示:
根据题意可得:BF=DE=1,EF=BD=5,BC=1,AC=AE,
设旗杆AB高为x米,则AF=(x-1)米,
在Rt△ABC中,AC2=AB2+BC2,
∴AC2=x2+1,
在Rt△AEF中,AE2=AF2+EF2,
∴x2+1=(x-1)2+52,
解得:x=12.5,
答:学校旗杆的高度为12.5米,
故答案为:12.5.
【分析】过点E作EF⊥AB于F,设旗杆AB高为x米,则AF=(x-1)米,利用勾股定理可得AC2=x2+1,x2+1=(x-1)2+52,再求出x的值即可.
19.【答案】由题意可知解得c=8,∴|b-10|+ =0,
∴b- 10=0,2c-a- 10=0,∴b= 10,a=6
∵a2+c2=b2 .
∴该三角形是直角三角形,
∴此三角形的面积为×6×8= 24.
【解析】【分析】利用二次根式被开方数的非负性得出:c=8,在根据二次根式和绝对值都具有非负性得出b= 10,a=6,根据勾股定理的逆定理判断出三角形为直角三角形。
20.【答案】(1)解:如图,连接,
,
答:居民从点到点将少走路程;
(2),
是直角三角形,,
,
,
答:这片绿地的面积是.
【解析】【分析】(1)构造直角三角形,用勾股定理求解。连接,利用勾股定理求出;
(2)先根据勾股定理逆定理证明是直角三角形,,再根据三角形的面积公式即可求解.
1 / 1
一、选择题
1.如图,由六个边长为的小正方形构成一个大长方形,连接小正方形的三个顶点,可得到,则中边上的高是( )
A. B. C. D.
2.如图,长方形中,,,在数轴上,若以点为圆心,的长为半径作弧交数轴于点,则点表示的数为
A. B. C.2 D.
3. 小华新买了一条跳绳,如图1,他按照体育老师教的方法确定适合自己的绳长:一脚踩住绳子的中央,手肘靠近身体,两肘弯屈,小臂水平转向两侧,两手将绳拉直,绳长即合适长度。将图1抽象成如图2,若两手握住的绳柄两端距离约为1米,小臂到地面的距离约1. 2米,则适合小华的绳长为( )
A.2. 2米 B.2. 4米 C.2. 6米 D.2. 8米
4.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大的正方形内,若知道图中阴影部分的面积,则一定能求出( )
A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
5.以下列数据为长度的线段中,可以构成直角三角形的是( )
A.1,, B.,3,5 C.1,2,3 D.2,3,4
6.下列是勾股数的是
A.12,15,18 B.6,10,7 C.12,16,20 D.,,
7.下列各组数中不能作为直角三角形的三边长的是( )
A.2,3,4 B.3,4,5 C.5,12,13 D.7,24,25
8.如图,这是一个供滑板爱好者使用的型池的示意图,该型池可以看作是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为的半圆,其边缘,点在上,,一名滑板爱好者从点滑到点,则他滑行的最短距离为( )m(边缘部分的厚度可以忽略不计,取3)
A.17 B. C. D.
二、填空题
9.如图,在数轴上点表示的实数是 .
10.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为,较短直角边长为,若,大正方形的面积为,则小正方形的边长为 .
11.一艘轮船8:00从A港出发向西航行,10:00折向北航行,平均航速均为20千米/时,则11:30时该轮船离A港的距离为 .
12.如图,将长为的弹性绳放置在直线上,固定端点和,然后把中点竖直向上拉升至点,则拉长后弹性绳的长为 .
13.如图,已知圆柱底面的周长为6dm,圆柱高为4dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为
14.《九章算术》中一道“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”题意是:有一个池塘,其水面是边长为10尺的正方形,一棵芦苇AC生长在它的中央,高出水面部分BC为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部C恰好碰到岸边的C'处(如图),求水深和芦苇长各多少尺?该问题中的水深为 尺.
三、解答题
15.有一架秋千,当它静止时,踏板离地的垂直高度DE=0.5m,将它往前推送2m(水平距离BC=2m)时,秋千的踏板离地的垂直高度BF=1.5m,秋千的绳索始终拉得很直,求绳索AD的长度
16.如图,在平面直角坐标系中,A(1,1),B(3,1),C(1,5)是三角形的三个顶点,求BC的长.
17.如图,在四边形ABCD中,∠ABC=120°,AB⊥AD,BC⊥CD,AB=4,CD=5.求四边形ABCD的面积.
18. 同学们想利用升旗的绳子、卷尺,测算学校旗杆的高度.爱动脑的小华设计了这样一个方案:如图,将升旗的绳子拉直刚好触底,此时测得绳子末端C到旗杆AB的底端B的距离为1米,然后将绳子末端拉直到距离旗杆5米的点E处,此时测得绳子末端E距离地面的高度为1米.请你根据小华的测量方案和测量数据,求出学校旗杆的高度.
19.已知a,b,c分别为三角形的三边长,且a,b,c满足|b-10|+=,求此三角形的面积.
20.某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角建造了一块绿化地(阴影部分).如图,已知,技术人员通过测量确定了.
(1)小区内部分居民每天必须从点经过点再到点位置,为了方便居民出人,技术人员打算在绿地中开辟一条从点直通点的小路,请问如果方案落实施工完成,居民从点到点将少走多少路程?
(2)这片绿地的面积是多少?
答案解析部分
1.【答案】A
【解析】【解答】解:设中边上的高为h,
由勾股定理,得,
∵,,
即,
解得:
故中边上的高是.
故答案为:A.
【分析】根据勾股定理求出,根据题意得出的面积等于正方形面积减去其他3个三角形的面积,再利用三角形等面积法求出三角形的高即可.
2.【答案】A
【解析】【解答】解:∵四边形ABCD是长方形,
∴∠B=90°,BC=AD=1,
∴,
∵ 以点A为圆心,AC的长为半径作弧交数轴于点M,
∴AM=AC=,
∵点A所表示的数为-1,
∴点M到原点的距离为,
又∵点M在原点的右边,
∴点M表示的数为.
故答案为:A.
【分析】由矩形的性质得∠B=90°,BC=AD=1,进而由勾股定理算出AC=,由同圆的半径相等得AM=AC=,然后找出点M到原点的距离,并结合点M在原点的右边即可得出点M所表示的数.
3.【答案】C
【解析】【解答】解:标字母如图所示,过C作CD⊥AB于点D.
由题意得:AC=BC,AB=1米,
∴AD=BD=0.5(米).
在Rt△BCD中,∴BD=1.2米,
∴BC=AC===1.3(米),
∴绳长为1.3×2=2.6(米).
故答案为:C.
【分析】由题意得出图形是等腰三角形,再根据等腰三角形“三线合一”的性质和勾股定理求解即可.
4.【答案】C
【解析】【解答】解:设直角三角形的各边长为a,b,c,满足a2+c2=c2,
可以得到:阴影部分面积+小正方形面积+大正方形面积-重叠部分面积=最大正方形面积,
即:阴影部分面积+a2+b2-重叠部分面积=c2.
所以有阴影部分面积=重叠部分面积.
故答案为:C.
【分析】结合勾股定理的几何意义,将三个正方形的面积联系起来,再用两种方法表示出最大正方形的面积,问题得到解决.
5.【答案】A
【解析】【解答】A:正确.
B:,错误.
C:
D:
故答案为A.
【分析】用勾股定理逆定理,关键是掌握如果三角形的三边长a,b,c满足,那么这个三角形就是直角三角形,
据此先求出两小边的平方和,再求出最长边的平方,最后看看是否相等即可.
6.【答案】C
【解析】【解答】解:A、∵122+152=144+225=369≠182=364,∴ 12,15,18不是一组勾股数,故此选项不符合题意;
B、∵62+72=36+49=85≠102=100,∴ 6,10,7不是一组勾股数,故此选项不符合题意;
C、∵122+162=144+256=400=202,∴ 12,16,20是一组勾股数,故此选项符合题意;
D、∵,, 不是一组正整数,∴不是一组勾股数,故此选项不符合题意.
故答案为:C.
【分析】能够构成一个直角三角形三边的三个正整数就是勾股数,据此逐项判断得出答案.
7.【答案】A
8.【答案】B
【解析】【解答】解:将半圆面展开可得:
米,米,
在中,由勾股定理得米,
即滑行的最短距离为米,
故答案为:B.
【分析】将半圆面展开可得,、、三点构成直角三角形,为斜边,为半圆的长,,根据勾股定理计算求解即可.
9.【答案】
【解析】【解答】解:由图形得OB==,
∴OA=OB=,
∴ 在数轴上点表示的实数是- .
故答案为:-.
【分析】由勾股定理求出OB=,即得OA=OB=,继而得解.
10.【答案】3
【解析】【解答】解:由题意知:中间小正方形的边长为:a -b
∵每一个直角三角形的面积为:ab=x8=4
∴4xab+(a-b)2=25
∴(a-b)2=25-16=9
∴a-b=3或a-b=-3(舍去)
故答案为:3.
【分析】本题主要考查勾股定理,熟练运用勾股定理及完全平方公式是解题的关键.
11.【答案】50千米
12.【答案】
【解析】【解答】解:∵占C是AB的中点,
∴AC=CB=6cm,
在中,(cm)
∴拉长后弹性绳的长为 :AD+BD=2AD=15cm。
故答案为:15cm。
【分析】根据勾股定理计算即可。
13.【答案】10dm
【解析】【解答】解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.
∵圆柱底面的周长为6dm,圆柱高为4dm,
∴AB=4dm,BC=BC′=3dm,
∴AC2=42+32=25,
∴AC=5dm,
∴这圈金属丝的周长最小为2AC=10dm.
故答案为:10dm
【分析】要求丝线的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,根据勾股定理计算即可.
14.【答案】12
【解析】【解答】解:依题意画出图形,
设芦苇长AC=AC′=x尺,
则水深AB=(x﹣1)尺,
∵C′E=10尺,
∴C′B=5尺,
在Rt△AC′B中,
52+(x﹣1)2=x2,
解得:x=13,
即芦苇长13尺,水深为12尺,
故答案为:12.
【分析】首先把事物图抽象数学几何图形,由图根据题意,可知EC′的长为10尺,从而求得C′B=5尺,然后设芦苇长AC=AC′=x尺,则水深AB为(x﹣1)尺,根据勾股定理列出方程,求解即可得到芦苇的长和水深.
15.【答案】解:在Rt△ACB中,AC2+BC2=AB2,
设秋千的绳索长为xm,则AC=(x﹣1)m,
故x2=22+(x﹣1)2,
解得:x=2.5,
答:绳索AD的长度是2.5m.
【解析】【分析】 设秋千的绳索长为xm,得出AC=(x﹣1)m, 利用勾股定理得出AC2+BC2=AB2, 从而得出关于x的方程,解方程求出x的值,即可得出答案.
16.【答案】解:∵A(1,1),B(3,1),C(1,5),
∴AC=5-1=4,AB=3-1=2,
在Rt△ABC中,
.
【解析】【分析】根据点A、B、C的坐标求出AB、AC的长度,再利用直角三角形中,两条直角边长的平方之和一定等于斜边长的平方列式计算即可求解.
17.【答案】9
18.【答案】解:12.5米
【解析】【解答】过点E作EF⊥AB于F,如图所示:
根据题意可得:BF=DE=1,EF=BD=5,BC=1,AC=AE,
设旗杆AB高为x米,则AF=(x-1)米,
在Rt△ABC中,AC2=AB2+BC2,
∴AC2=x2+1,
在Rt△AEF中,AE2=AF2+EF2,
∴x2+1=(x-1)2+52,
解得:x=12.5,
答:学校旗杆的高度为12.5米,
故答案为:12.5.
【分析】过点E作EF⊥AB于F,设旗杆AB高为x米,则AF=(x-1)米,利用勾股定理可得AC2=x2+1,x2+1=(x-1)2+52,再求出x的值即可.
19.【答案】由题意可知解得c=8,∴|b-10|+ =0,
∴b- 10=0,2c-a- 10=0,∴b= 10,a=6
∵a2+c2=b2 .
∴该三角形是直角三角形,
∴此三角形的面积为×6×8= 24.
【解析】【分析】利用二次根式被开方数的非负性得出:c=8,在根据二次根式和绝对值都具有非负性得出b= 10,a=6,根据勾股定理的逆定理判断出三角形为直角三角形。
20.【答案】(1)解:如图,连接,
,
答:居民从点到点将少走路程;
(2),
是直角三角形,,
,
,
答:这片绿地的面积是.
【解析】【分析】(1)构造直角三角形,用勾股定理求解。连接,利用勾股定理求出;
(2)先根据勾股定理逆定理证明是直角三角形,,再根据三角形的面积公式即可求解.
1 / 1
