2023-2024学年数学沪科版七年级上册 课时提高练 1.2 课时3 绝对值(含答案)
文档属性
| 名称 | 2023-2024学年数学沪科版七年级上册 课时提高练 1.2 课时3 绝对值(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 55.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-20 00:00:00 | ||
图片预览

文档简介
1.2 课时3 绝对值
【练基础】
必备知识1 绝对值的概念及性质
1.-9的绝对值是 ( )
A.9 B.-9
C. D.-
2.计算|-4|的结果是 ( )
A.4 B.-4
C.±4 D.±2
3.下列说法错误的是 ( )
A.一个正数的绝对值一定是正数
B.任何数的绝对值都是正数
C.一个负数的绝对值一定是正数
D.任何数的绝对值都不是负数
4.若绝对值相等的两个数在数轴上对应的两点之间的距离为8,则这两个数为 ( )
A.+8或-8 B.+4或-4
C.-4或+8 D.-8或+4
5.数a的绝对值一定是 ( )
A.非负数 B.负数
C.非正数 D.正数
6.若一个数的绝对值等于3,则这个数是 ( )
A.3 B.-3
C.±3 D.
7.绝对值不大于4的整数有 个.
8.若|a|+|b-2|=0,则a= ,b= .
9.计算:
(1)2.7+|-2.7|-|-2.7|;
(2)|-16|+|+36|-|-1|.
必备知识2 绝对值的实际应用
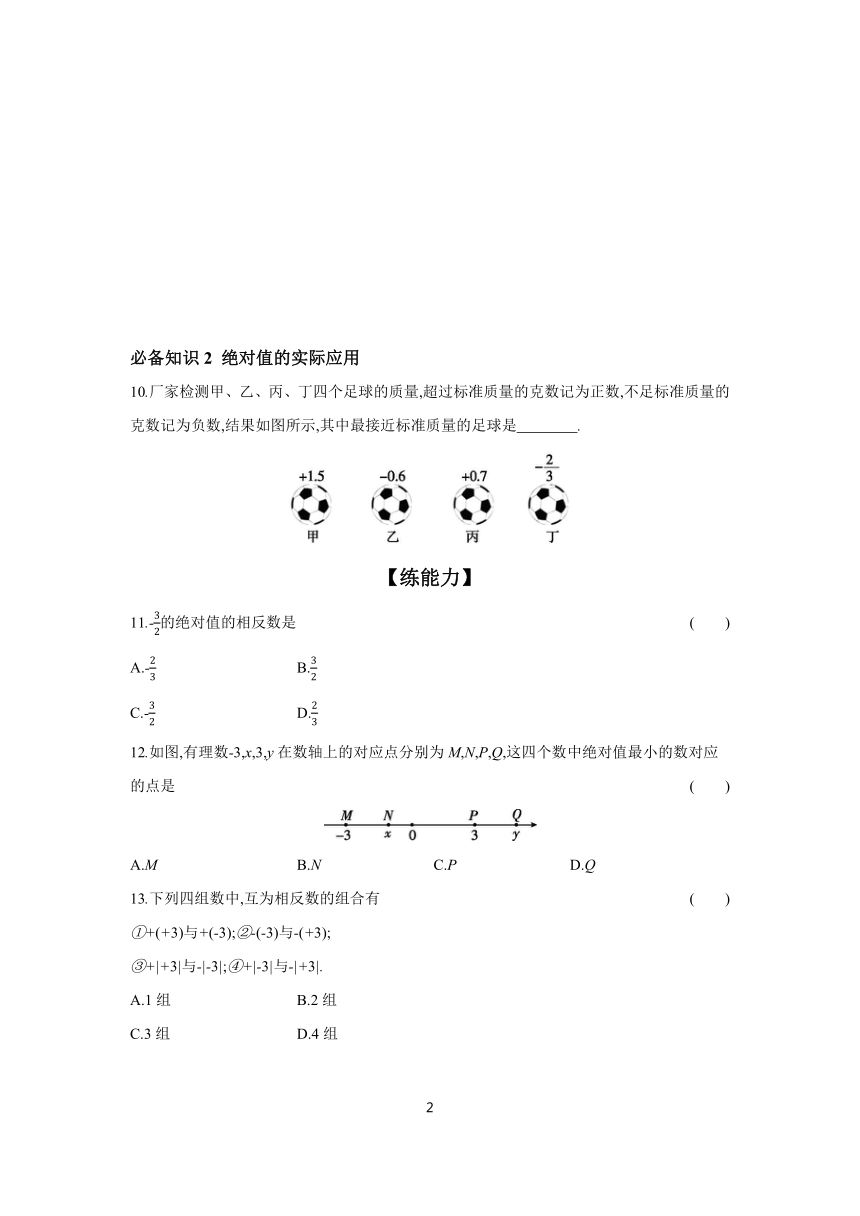
10.厂家检测甲、乙、丙、丁四个足球的质量,超过标准质量的克数记为正数,不足标准质量的克数记为负数,结果如图所示,其中最接近标准质量的足球是 .
【练能力】
11.-的绝对值的相反数是 ( )
A.- B.
C.- D.
12.如图,有理数-3,x,3,y在数轴上的对应点分别为M,N,P,Q,这四个数中绝对值最小的数对应的点是 ( )
A.M B.N C.P D.Q
13.下列四组数中,互为相反数的组合有 ( )
①+(+3)与+(-3);②-(-3)与-(+3);
③+|+3|与-|-3|;④+|-3|与-|+3|.
A.1组 B.2组
C.3组 D.4组
14.某汽车配件厂生产一批圆形的零件,从中随机抽取6件进行检验,并规定比标准直径长的毫米数记作正数,比标准直径短的毫米数记作负数.检验结果记录如下:
零件编号 1 2 3 4 5 6
检验结果 +0.5 -0.3 +0.1 0 -0.1 +0.2
(1)哪些零件的质量相对来说好一些 用学过的绝对值知识进行说明.
(2)若规定与标准直径相差不大于0.2毫米的零件为合格产品,则这6件产品中有几件不合格
15.已知a,b,c为有理数,且它们在数轴上的位置如图所示.
(1)试判断a,b,c的正负性.
(2)在数轴上标出a,b,c的相反数的位置.
(3)根据数轴化简:
①|a|= ;②|b|= ;
③|c|= ;④|-a|= ;
⑤|-b|= ;⑥|-c|= .
(4)若|a|=5.5,|b|=2.5,|c|=5,求a,b,c的值.
【练素养】
16.【观察与归纳】
(1)观察下列各式的大小关系:
|-2|+|3|>|-2+3|;
|-8|+|3|>|-8+3|;
|-2|+|-3|=|-2-3|;
|0|+|-6|=|0-6|.
归纳:|a|+|b| |a+b|.(用“>”、“<”、“=”、“≥”或“≤”填空)
【理解与应用】
(2)根据上题中得出的结论,若|m|+|n|=9,|m+n|=1,求m的值.
参考答案
基础演练
1.A 2.A 3.B 4.B 5.A 6.C
7.9 8.0 2
9.【解析】(1)原式=2.7+2.7-2.7=2.7.
(2)原式=16+36-1=51.
10.乙
能力生成
11.C 12.B
13.D 【解析】①+(+3)=3,+(-3)=-3,互为相反数;②-(-3)=3,-(+3)=-3,互为相反数;③+|+3|=3,-|-3|=-3,互为相反数;④+|-3|=3,-|+3|=-3,互为相反数.故选D.
14.【解析】(1)第3,4,5件的零件质量相对来说好一些,因为绝对值越小越接近标准尺寸.
(2)这6件产品中有2件产品不合格.
15.(3)①-a ②b ③c ④-a ⑤b ⑥c
【解析】(1)由数轴可得a是负数,b,c是正数.
(2)略.
(4)因为|a|=5.5,|b|=2.5,|c|=5,
a是负数,b,c是正数,
所以a=-5.5,b=2.5,c=5.
素养通关
16.【解析】(1)≥.
(2)由上题结论可知,因为|m|+|n|=9,|m+n|=1,|m|+|n|≠|m+n|,所以m、n 异号.
①当m为正数,n为负数时,m-n=9,则n=m-9,|m+m-9|=1,m=5或4;
②当m为负数,n为正数时,-m+n=9,则n=m+9,|m+m+9|=1,m=-4或-5.
综上所述,m为±4或±5.
2
【练基础】
必备知识1 绝对值的概念及性质
1.-9的绝对值是 ( )
A.9 B.-9
C. D.-
2.计算|-4|的结果是 ( )
A.4 B.-4
C.±4 D.±2
3.下列说法错误的是 ( )
A.一个正数的绝对值一定是正数
B.任何数的绝对值都是正数
C.一个负数的绝对值一定是正数
D.任何数的绝对值都不是负数
4.若绝对值相等的两个数在数轴上对应的两点之间的距离为8,则这两个数为 ( )
A.+8或-8 B.+4或-4
C.-4或+8 D.-8或+4
5.数a的绝对值一定是 ( )
A.非负数 B.负数
C.非正数 D.正数
6.若一个数的绝对值等于3,则这个数是 ( )
A.3 B.-3
C.±3 D.
7.绝对值不大于4的整数有 个.
8.若|a|+|b-2|=0,则a= ,b= .
9.计算:
(1)2.7+|-2.7|-|-2.7|;
(2)|-16|+|+36|-|-1|.
必备知识2 绝对值的实际应用
10.厂家检测甲、乙、丙、丁四个足球的质量,超过标准质量的克数记为正数,不足标准质量的克数记为负数,结果如图所示,其中最接近标准质量的足球是 .
【练能力】
11.-的绝对值的相反数是 ( )
A.- B.
C.- D.
12.如图,有理数-3,x,3,y在数轴上的对应点分别为M,N,P,Q,这四个数中绝对值最小的数对应的点是 ( )
A.M B.N C.P D.Q
13.下列四组数中,互为相反数的组合有 ( )
①+(+3)与+(-3);②-(-3)与-(+3);
③+|+3|与-|-3|;④+|-3|与-|+3|.
A.1组 B.2组
C.3组 D.4组
14.某汽车配件厂生产一批圆形的零件,从中随机抽取6件进行检验,并规定比标准直径长的毫米数记作正数,比标准直径短的毫米数记作负数.检验结果记录如下:
零件编号 1 2 3 4 5 6
检验结果 +0.5 -0.3 +0.1 0 -0.1 +0.2
(1)哪些零件的质量相对来说好一些 用学过的绝对值知识进行说明.
(2)若规定与标准直径相差不大于0.2毫米的零件为合格产品,则这6件产品中有几件不合格
15.已知a,b,c为有理数,且它们在数轴上的位置如图所示.
(1)试判断a,b,c的正负性.
(2)在数轴上标出a,b,c的相反数的位置.
(3)根据数轴化简:
①|a|= ;②|b|= ;
③|c|= ;④|-a|= ;
⑤|-b|= ;⑥|-c|= .
(4)若|a|=5.5,|b|=2.5,|c|=5,求a,b,c的值.
【练素养】
16.【观察与归纳】
(1)观察下列各式的大小关系:
|-2|+|3|>|-2+3|;
|-8|+|3|>|-8+3|;
|-2|+|-3|=|-2-3|;
|0|+|-6|=|0-6|.
归纳:|a|+|b| |a+b|.(用“>”、“<”、“=”、“≥”或“≤”填空)
【理解与应用】
(2)根据上题中得出的结论,若|m|+|n|=9,|m+n|=1,求m的值.
参考答案
基础演练
1.A 2.A 3.B 4.B 5.A 6.C
7.9 8.0 2
9.【解析】(1)原式=2.7+2.7-2.7=2.7.
(2)原式=16+36-1=51.
10.乙
能力生成
11.C 12.B
13.D 【解析】①+(+3)=3,+(-3)=-3,互为相反数;②-(-3)=3,-(+3)=-3,互为相反数;③+|+3|=3,-|-3|=-3,互为相反数;④+|-3|=3,-|+3|=-3,互为相反数.故选D.
14.【解析】(1)第3,4,5件的零件质量相对来说好一些,因为绝对值越小越接近标准尺寸.
(2)这6件产品中有2件产品不合格.
15.(3)①-a ②b ③c ④-a ⑤b ⑥c
【解析】(1)由数轴可得a是负数,b,c是正数.
(2)略.
(4)因为|a|=5.5,|b|=2.5,|c|=5,
a是负数,b,c是正数,
所以a=-5.5,b=2.5,c=5.
素养通关
16.【解析】(1)≥.
(2)由上题结论可知,因为|m|+|n|=9,|m+n|=1,|m|+|n|≠|m+n|,所以m、n 异号.
①当m为正数,n为负数时,m-n=9,则n=m-9,|m+m-9|=1,m=5或4;
②当m为负数,n为正数时,-m+n=9,则n=m+9,|m+m+9|=1,m=-4或-5.
综上所述,m为±4或±5.
2
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
