2023-2024学年数学沪科版七年级上册 第4章 直线与角 自我评估(含解析)
文档属性
| 名称 | 2023-2024学年数学沪科版七年级上册 第4章 直线与角 自我评估(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 134.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-20 00:00:00 | ||
图片预览



文档简介
第4章 直线与角 自我评估
(建议用时:90分钟 分值:150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.与图中实物相类似的立体图形分别是 ( )
A.球,圆锥,棱锥
B.圆,圆柱,圆锥
C.球,棱柱,棱锥
D.球,圆柱,圆锥
2.与30°的角互为补角的角的度数是 ( )
A.30° B.60° C.120° D.150°
3.下列画图属于尺规作图的是 ( )
A.用量角器画出∠AOB的平分线
B.作∠AOB,使∠AOB=3∠1
C.用三角板画∠AOB=90°
D.画线段AB=3 cm
4.下列几何体中,面的个数最少的是 ( )
5.下列说法中,正确的是 ( )
A.延长射线OA B.延长直线AB
C.延长线段AB D.作直线AB=CD
6.如图,已知线段AB,在BA的延长线上取一点C,使CA=3AB,则线段CA与线段CB的长度之比为 ( )
A.3∶4 B.2∶3
C.3∶5 D.1∶2
7.如图,∠AOB=120°,∠BOC=30°,OD是∠AOC的角平分线,则∠BOD= ( )
A.45° B.75°
C.85° D.90°
8.8点30分时,钟表的时针与分针所成的最小角的度数为 ( )
A.30° B.45°
C.60° D.75°
9.拼尽全力挥动翅膀,才能在常仰望的天空中去拥抱梦想.如图中展翅欲飞的小鸟是利用直尺画出线段及其延长线构成的,就该图中出现的线段、直线、射线的条数而言 ( )
A.线段最多 B.直线最多
C.射线最多 D.射线最少
10.如图,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在同一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在 ( )
A.点A
B.点B
C.AB之间
D.BC之间
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知∠A=40°,则∠A的余角等于 °.
12.我们经常以“度”为单位来度量角,但在军事上通常以“密位”为单位来度量角的大小,就是把周角等分成6000份,每一份叫做1密位的角,所以直角= 密位.
13.【拱墅区期末】从起始站A市坐火车到终点站G市中途共停靠5次,各站点到A市的距离如下:
站点 B C D E F G
距A市距离 (千米) 445 805 1135 1495 1825 2270
若火车车票的价格由路程决定,则沿途总共有 种不同的票价.
14.已知A,B,C三点在同一条直线上,AB=8,BC=6,M,N分别是AB、BC的中点,则线段MN的长是 .
三、(本大题共2小题,每小题8分,满分16分)
15.计算:182°36'÷4+22°16'×3.
16.【芜湖期末】如图,AB=18 cm,C是线段AB的三等分点,D是线段CB上一点,CD比DB长4 cm,求CD的长.
四、(本大题共2小题,每小题8分,满分16分)
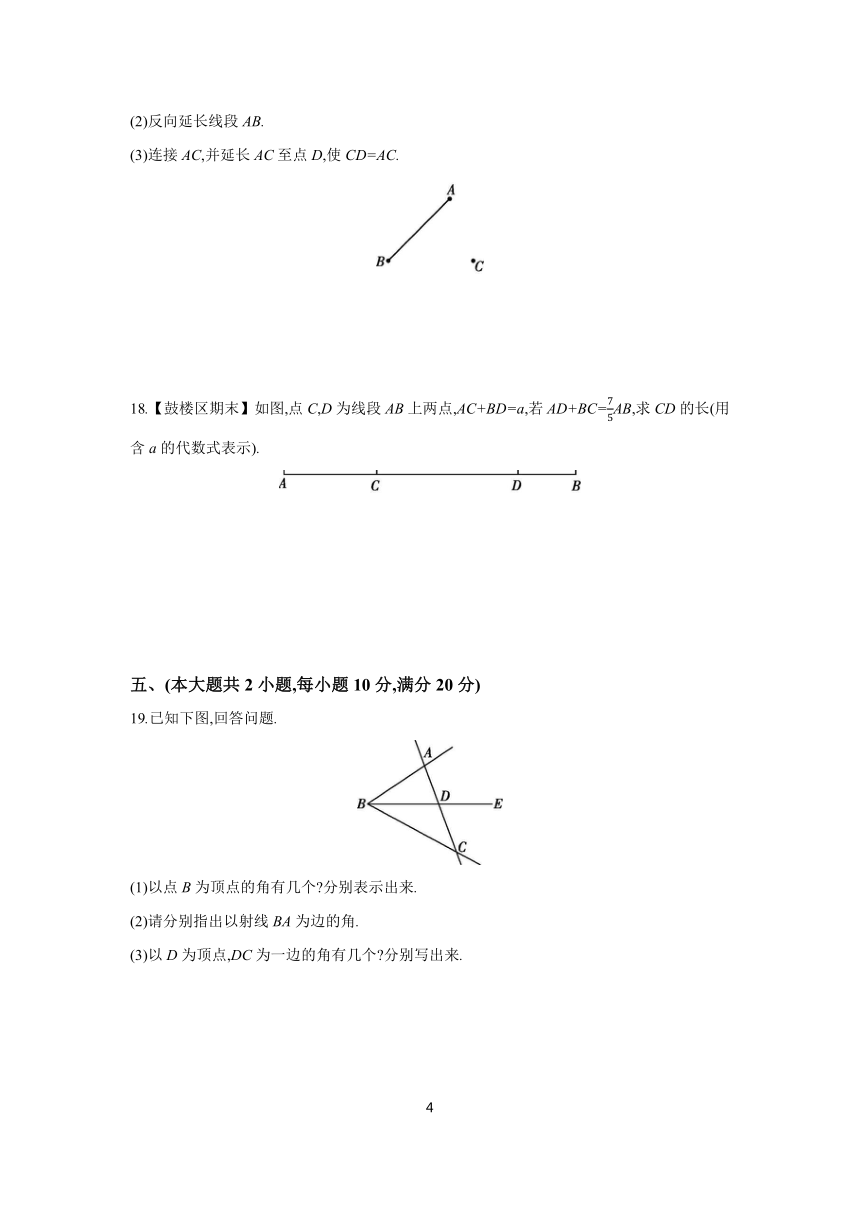
17.如图,C是线段AB外一点,按要求画图.
(1)画射线CB.
(2)反向延长线段AB.
(3)连接AC,并延长AC至点D,使CD=AC.
18.【鼓楼区期末】如图,点C,D为线段AB上两点,AC+BD=a,若AD+BC=AB,求CD的长(用含a的代数式表示).
五、(本大题共2小题,每小题10分,满分20分)
19.已知下图,回答问题.
(1)以点B为顶点的角有几个 分别表示出来.
(2)请分别指出以射线BA为边的角.
(3)以D为顶点,DC为一边的角有几个 分别写出来.
20.如图,这是一个几何体的表面展开图.
(1)该几何体的名称是 ,其底面半径为 .
(2)根据图中所给信息,求该几何体的表面积和体积.(结果保留π)
六、(本题满分12分)
21.如图,直线AE上有一点O,∠AOB=30°,∠BOC=∠AOB.
(1)求∠EOC的度数.
(2)如果OD平分∠EOC,求∠BOD的度数.
七、(本题满分12分)
22.在一条不完整的数轴上从左到右依次有点A,B,D,C(如图所示),其中AB=2,BD=3,DC=1,设点A,B,D,C所对应数的和是p.
(1)若以B为原点.写出点A,D,C所对应的数,并计算p的值.
(2)若原点O在图中数轴上点C的右边,且CO=x,p=-71,求x的值.
八、(本题满分14分)
23.已知点O在直线AB上,∠BOD与∠COD互补.
(1)如图1,试说明:OD平分∠AOC.
图1
(2)如图2,若∠AOE=∠BOD,∠COE=3∠AOC,求∠BOE的度数.
图2
参考答案
1.D 2.D 3.B 4.C 5.C 6.A 7.B 8.D
9.C 【解析】由图可得,线段有14条,直线有2条,射线有16条.
10.A 【解析】①以点A为停靠点,则所有人的路程的和=15×300+10×900=13500(米),
②以点B为停靠点,则所有人的路程的和=30×300+10×600=15000(米),
③以点C为停靠点,则所有人的路程的和=30×900+15×600=36000(米),
④当在AB之间停靠时,设停靠点到A的距离是m(013500,
⑤当在BC之间停靠时,设停靠点到B的距离为n(013500.
所以该停靠点的位置应设在点A.
11.50 12.1500 13.14
14.7或1 【解析】由AB=8,BC=6,M、N分别为AB、BC中点,得MB=AB=4,NB=BC=3.
①C在线段AB的延长线上,MN=MB+NB=4+3=7;
②C在线段AB上,MN=MB-NB=4-3=1;
③C在线段AB的反延长线上,AB>BC,不成立,
综上所述,线段MN的长为7或1.
15.【解析】原式=45°+(2°+36')÷4+66°48'
=45°+156'÷4+66°48'
=45°+39'+66°48'
=112°27'.
16.【解析】因为C是线段AB的三等分点,
所以AC=6(cm),BC=AB-AC=12(cm).
又因为CD+DB=BC,CD=DB+4,
所以DB+4+DB=BC,2DB+4=12,DB=4,
所以CD=AB-AC-DB=18-6-4=8(cm).
17.【解析】如图所示.
18.【解析】因为AD+BC=AB,所以AC+CD+CD+DB=(AC+CD+DB).
因为AC+BD=a,所以a+2CD=(a+CD),
所以CD=a.
19.【解析】(1)以点B为顶点的角有∠ABC,∠ABD,∠DBC,共3个.
(2)以射线BA为边的角有∠ABE,∠ABC.
(3)以D为顶点,DC为一边的角有∠BDC,∠EDC,共2个.
20.【解析】(1)圆柱;1.
(2)该几何体的表面积为2×π×12+2π×1×3=8π,
该几何体的体积=π×12×3=3π.
21.【解析】(1)因为∠AOB=30°,∠BOC=∠AOB,
所以∠AOC=2∠AOB=60°,所以∠EOC=120°.
(2)因为∠EOC=120°,OD平分∠EOC,
所以∠COD=∠EOC=60°,
所以∠BOD=∠COB+∠COD=30°+60°=90°.
22.【解析】(1)点A,D,C所对应的数分别为-2,3,4,
p=-2+3+4=5.
(2)A,B,D,C表示的数分别为
-6-x,-4-x,-1-x,-x,
得-6-x-4-x-1-x-x=-71,
解得x=15.
23.【解析】(1)因为点O在直线AB上,
所以∠AOB=180°,
所以∠AOD+∠BOD=∠AOB=180°.
因为∠BOD与∠COD互补,
所以∠BOD+∠COD=180°,
所以∠AOD=∠COD,
所以OD平分∠AOC.
(2)因为∠AOE=∠BOD,
所以∠AOE-∠DOE=∠BOD-∠DOE,
所以∠AOD=∠COD=∠BOE.
设∠AOD=∠COD=∠BOE=m,
所以∠AOC=∠AOD+∠COD=2m.
因为∠COE=3∠AOC,
所以∠COE=3×2m=6m.
因为∠AOC+∠COE+∠BOE=∠AOB=180°,
所以2m+6m+m=180°,
解得m=20°,即∠BOE=20°.
2
(建议用时:90分钟 分值:150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.与图中实物相类似的立体图形分别是 ( )
A.球,圆锥,棱锥
B.圆,圆柱,圆锥
C.球,棱柱,棱锥
D.球,圆柱,圆锥
2.与30°的角互为补角的角的度数是 ( )
A.30° B.60° C.120° D.150°
3.下列画图属于尺规作图的是 ( )
A.用量角器画出∠AOB的平分线
B.作∠AOB,使∠AOB=3∠1
C.用三角板画∠AOB=90°
D.画线段AB=3 cm
4.下列几何体中,面的个数最少的是 ( )
5.下列说法中,正确的是 ( )
A.延长射线OA B.延长直线AB
C.延长线段AB D.作直线AB=CD
6.如图,已知线段AB,在BA的延长线上取一点C,使CA=3AB,则线段CA与线段CB的长度之比为 ( )
A.3∶4 B.2∶3
C.3∶5 D.1∶2
7.如图,∠AOB=120°,∠BOC=30°,OD是∠AOC的角平分线,则∠BOD= ( )
A.45° B.75°
C.85° D.90°
8.8点30分时,钟表的时针与分针所成的最小角的度数为 ( )
A.30° B.45°
C.60° D.75°
9.拼尽全力挥动翅膀,才能在常仰望的天空中去拥抱梦想.如图中展翅欲飞的小鸟是利用直尺画出线段及其延长线构成的,就该图中出现的线段、直线、射线的条数而言 ( )
A.线段最多 B.直线最多
C.射线最多 D.射线最少
10.如图,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在同一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在 ( )
A.点A
B.点B
C.AB之间
D.BC之间
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知∠A=40°,则∠A的余角等于 °.
12.我们经常以“度”为单位来度量角,但在军事上通常以“密位”为单位来度量角的大小,就是把周角等分成6000份,每一份叫做1密位的角,所以直角= 密位.
13.【拱墅区期末】从起始站A市坐火车到终点站G市中途共停靠5次,各站点到A市的距离如下:
站点 B C D E F G
距A市距离 (千米) 445 805 1135 1495 1825 2270
若火车车票的价格由路程决定,则沿途总共有 种不同的票价.
14.已知A,B,C三点在同一条直线上,AB=8,BC=6,M,N分别是AB、BC的中点,则线段MN的长是 .
三、(本大题共2小题,每小题8分,满分16分)
15.计算:182°36'÷4+22°16'×3.
16.【芜湖期末】如图,AB=18 cm,C是线段AB的三等分点,D是线段CB上一点,CD比DB长4 cm,求CD的长.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,C是线段AB外一点,按要求画图.
(1)画射线CB.
(2)反向延长线段AB.
(3)连接AC,并延长AC至点D,使CD=AC.
18.【鼓楼区期末】如图,点C,D为线段AB上两点,AC+BD=a,若AD+BC=AB,求CD的长(用含a的代数式表示).
五、(本大题共2小题,每小题10分,满分20分)
19.已知下图,回答问题.
(1)以点B为顶点的角有几个 分别表示出来.
(2)请分别指出以射线BA为边的角.
(3)以D为顶点,DC为一边的角有几个 分别写出来.
20.如图,这是一个几何体的表面展开图.
(1)该几何体的名称是 ,其底面半径为 .
(2)根据图中所给信息,求该几何体的表面积和体积.(结果保留π)
六、(本题满分12分)
21.如图,直线AE上有一点O,∠AOB=30°,∠BOC=∠AOB.
(1)求∠EOC的度数.
(2)如果OD平分∠EOC,求∠BOD的度数.
七、(本题满分12分)
22.在一条不完整的数轴上从左到右依次有点A,B,D,C(如图所示),其中AB=2,BD=3,DC=1,设点A,B,D,C所对应数的和是p.
(1)若以B为原点.写出点A,D,C所对应的数,并计算p的值.
(2)若原点O在图中数轴上点C的右边,且CO=x,p=-71,求x的值.
八、(本题满分14分)
23.已知点O在直线AB上,∠BOD与∠COD互补.
(1)如图1,试说明:OD平分∠AOC.
图1
(2)如图2,若∠AOE=∠BOD,∠COE=3∠AOC,求∠BOE的度数.
图2
参考答案
1.D 2.D 3.B 4.C 5.C 6.A 7.B 8.D
9.C 【解析】由图可得,线段有14条,直线有2条,射线有16条.
10.A 【解析】①以点A为停靠点,则所有人的路程的和=15×300+10×900=13500(米),
②以点B为停靠点,则所有人的路程的和=30×300+10×600=15000(米),
③以点C为停靠点,则所有人的路程的和=30×900+15×600=36000(米),
④当在AB之间停靠时,设停靠点到A的距离是m(0
⑤当在BC之间停靠时,设停靠点到B的距离为n(0
所以该停靠点的位置应设在点A.
11.50 12.1500 13.14
14.7或1 【解析】由AB=8,BC=6,M、N分别为AB、BC中点,得MB=AB=4,NB=BC=3.
①C在线段AB的延长线上,MN=MB+NB=4+3=7;
②C在线段AB上,MN=MB-NB=4-3=1;
③C在线段AB的反延长线上,AB>BC,不成立,
综上所述,线段MN的长为7或1.
15.【解析】原式=45°+(2°+36')÷4+66°48'
=45°+156'÷4+66°48'
=45°+39'+66°48'
=112°27'.
16.【解析】因为C是线段AB的三等分点,
所以AC=6(cm),BC=AB-AC=12(cm).
又因为CD+DB=BC,CD=DB+4,
所以DB+4+DB=BC,2DB+4=12,DB=4,
所以CD=AB-AC-DB=18-6-4=8(cm).
17.【解析】如图所示.
18.【解析】因为AD+BC=AB,所以AC+CD+CD+DB=(AC+CD+DB).
因为AC+BD=a,所以a+2CD=(a+CD),
所以CD=a.
19.【解析】(1)以点B为顶点的角有∠ABC,∠ABD,∠DBC,共3个.
(2)以射线BA为边的角有∠ABE,∠ABC.
(3)以D为顶点,DC为一边的角有∠BDC,∠EDC,共2个.
20.【解析】(1)圆柱;1.
(2)该几何体的表面积为2×π×12+2π×1×3=8π,
该几何体的体积=π×12×3=3π.
21.【解析】(1)因为∠AOB=30°,∠BOC=∠AOB,
所以∠AOC=2∠AOB=60°,所以∠EOC=120°.
(2)因为∠EOC=120°,OD平分∠EOC,
所以∠COD=∠EOC=60°,
所以∠BOD=∠COB+∠COD=30°+60°=90°.
22.【解析】(1)点A,D,C所对应的数分别为-2,3,4,
p=-2+3+4=5.
(2)A,B,D,C表示的数分别为
-6-x,-4-x,-1-x,-x,
得-6-x-4-x-1-x-x=-71,
解得x=15.
23.【解析】(1)因为点O在直线AB上,
所以∠AOB=180°,
所以∠AOD+∠BOD=∠AOB=180°.
因为∠BOD与∠COD互补,
所以∠BOD+∠COD=180°,
所以∠AOD=∠COD,
所以OD平分∠AOC.
(2)因为∠AOE=∠BOD,
所以∠AOE-∠DOE=∠BOD-∠DOE,
所以∠AOD=∠COD=∠BOE.
设∠AOD=∠COD=∠BOE=m,
所以∠AOC=∠AOD+∠COD=2m.
因为∠COE=3∠AOC,
所以∠COE=3×2m=6m.
因为∠AOC+∠COE+∠BOE=∠AOB=180°,
所以2m+6m+m=180°,
解得m=20°,即∠BOE=20°.
2
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
