五年级下册数学人教版3.2 长方体和正方体的表面积 同步练习(无答案)
文档属性
| 名称 | 五年级下册数学人教版3.2 长方体和正方体的表面积 同步练习(无答案) | 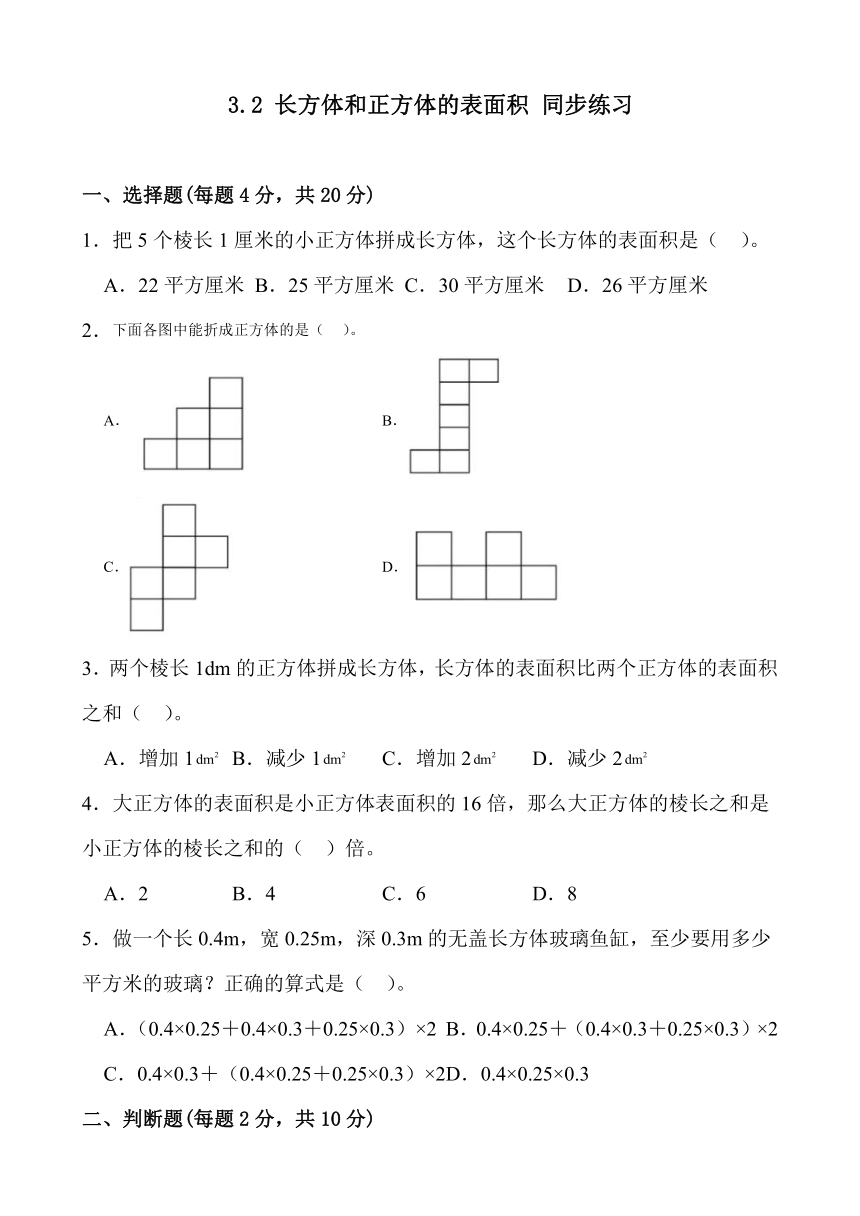 | |
| 格式 | docx | ||
| 文件大小 | 46.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 09:51:51 | ||
图片预览


文档简介
3.2 长方体和正方体的表面积 同步练习
一、选择题(每题4分,共20分)
1.把5个棱长1厘米的小正方体拼成长方体,这个长方体的表面积是( )。
A.22平方厘米 B.25平方厘米 C.30平方厘米 D.26平方厘米
2.下面各图中能折成正方体的是( )。
A. B.
C. D.
3.两个棱长1dm的正方体拼成长方体,长方体的表面积比两个正方体的表面积之和( )。
A.增加1 B.减少1 C.增加2 D.减少2
4.大正方体的表面积是小正方体表面积的16倍,那么大正方体的棱长之和是小正方体的棱长之和的( )倍。
A.2 B.4 C.6 D.8
5.做一个长0.4m,宽0.25m,深0.3m的无盖长方体玻璃鱼缸,至少要用多少平方米的玻璃?正确的算式是( )。
A.(0.4×0.25+0.4×0.3+0.25×0.3)×2 B.0.4×0.25+(0.4×0.3+0.25×0.3)×2
C.0.4×0.3+(0.4×0.25+0.25×0.3)×2 D.0.4×0.25×0.3
二、判断题(每题2分,共10分)
6.小明说他把长方体展开后发现了三个面是正方形. ( )
7.两个完全一样的长方体,拼成一个新的长方体后,表面积不变.( )
8.一个正方体的棱长总和是72分米,它的表面积是216平方分米。( )
9.求一个无盖的长方体鱼缸的表面积,就是求这个长方体前后左右和底面这5个面的面积.( )
10.一个无盖的长方体玻璃鱼缸,长50厘米、宽40厘米、高30厘米。做这个鱼缸至少需要玻璃74平方分米。( )
三、填空题(每题4分,共20分)
11.把一个长、宽、高分别为6分米、5分米、8分米的长方体切成两个完全相同的长方体,表面积最多可以增加( )平方分米。
12.一个棱长1米的正方体,沿长、宽、高各切三刀,三刀、四刀,恰好切成80个小长方体,这80个小长方体的表面积之和是( )平方厘米.
13.用长的铁丝做成一个长和宽都是的长方体框架,如果还需要在框架上给每个面糊上纸,那么一共需要( )的纸。
14.大正方体的表面积是小正方体表面积的16倍,那么大正方体的棱长之和是小正方体的棱长之和的( )倍。
15.要给3个长、宽、高分别为x、y、z的箱子打包,其打包方式如图所示,则打包带的总长至少要( )分米。(其中x=7分米,y=4分米,z=2分米。)
四、计算题(每题10分,共10分)
16.计算下列图形的表面积。(单位:dm)
(1) (2)
五、解答题(每题10分,共40分)
17.有一种无盖的玻璃鱼缸,长30厘米,宽20厘米,高15厘米,做这样一个鱼缸至少需要多少平方厘米的玻璃?
18.李叔叔用纸板做一个无盖的长方体纸盒。已经做好了两个相邻的面(如下图所示)。如果照这个规格接着做,可以制作一些不同的无盖纸盒,在这些不同的无盖纸盒中,需要纸板面积最大的是多少平方分米?
19.一根铁丝恰好可以焊接成一个长5厘米,宽3厘米,高4厘米的长方体框架。若这根铁丝也恰好能焊接成一个正方体框架。
(1)这个正方体框架的棱长是多少厘米?
(2)给这个正方体框架的表面焊接上铁皮,铁皮的面积是多少平方厘米?
20.学校要粉刷一间教室的四壁和天花。已知教室的长是9米,宽7米,高是3米,扣除门窗的面积12.5平方米,要粉刷的面积是多少平方米?如果每平方米需要花费4元涂料费,粉刷这个教室需要花费多少元?
一、选择题(每题4分,共20分)
1.把5个棱长1厘米的小正方体拼成长方体,这个长方体的表面积是( )。
A.22平方厘米 B.25平方厘米 C.30平方厘米 D.26平方厘米
2.下面各图中能折成正方体的是( )。
A. B.
C. D.
3.两个棱长1dm的正方体拼成长方体,长方体的表面积比两个正方体的表面积之和( )。
A.增加1 B.减少1 C.增加2 D.减少2
4.大正方体的表面积是小正方体表面积的16倍,那么大正方体的棱长之和是小正方体的棱长之和的( )倍。
A.2 B.4 C.6 D.8
5.做一个长0.4m,宽0.25m,深0.3m的无盖长方体玻璃鱼缸,至少要用多少平方米的玻璃?正确的算式是( )。
A.(0.4×0.25+0.4×0.3+0.25×0.3)×2 B.0.4×0.25+(0.4×0.3+0.25×0.3)×2
C.0.4×0.3+(0.4×0.25+0.25×0.3)×2 D.0.4×0.25×0.3
二、判断题(每题2分,共10分)
6.小明说他把长方体展开后发现了三个面是正方形. ( )
7.两个完全一样的长方体,拼成一个新的长方体后,表面积不变.( )
8.一个正方体的棱长总和是72分米,它的表面积是216平方分米。( )
9.求一个无盖的长方体鱼缸的表面积,就是求这个长方体前后左右和底面这5个面的面积.( )
10.一个无盖的长方体玻璃鱼缸,长50厘米、宽40厘米、高30厘米。做这个鱼缸至少需要玻璃74平方分米。( )
三、填空题(每题4分,共20分)
11.把一个长、宽、高分别为6分米、5分米、8分米的长方体切成两个完全相同的长方体,表面积最多可以增加( )平方分米。
12.一个棱长1米的正方体,沿长、宽、高各切三刀,三刀、四刀,恰好切成80个小长方体,这80个小长方体的表面积之和是( )平方厘米.
13.用长的铁丝做成一个长和宽都是的长方体框架,如果还需要在框架上给每个面糊上纸,那么一共需要( )的纸。
14.大正方体的表面积是小正方体表面积的16倍,那么大正方体的棱长之和是小正方体的棱长之和的( )倍。
15.要给3个长、宽、高分别为x、y、z的箱子打包,其打包方式如图所示,则打包带的总长至少要( )分米。(其中x=7分米,y=4分米,z=2分米。)
四、计算题(每题10分,共10分)
16.计算下列图形的表面积。(单位:dm)
(1) (2)
五、解答题(每题10分,共40分)
17.有一种无盖的玻璃鱼缸,长30厘米,宽20厘米,高15厘米,做这样一个鱼缸至少需要多少平方厘米的玻璃?
18.李叔叔用纸板做一个无盖的长方体纸盒。已经做好了两个相邻的面(如下图所示)。如果照这个规格接着做,可以制作一些不同的无盖纸盒,在这些不同的无盖纸盒中,需要纸板面积最大的是多少平方分米?
19.一根铁丝恰好可以焊接成一个长5厘米,宽3厘米,高4厘米的长方体框架。若这根铁丝也恰好能焊接成一个正方体框架。
(1)这个正方体框架的棱长是多少厘米?
(2)给这个正方体框架的表面焊接上铁皮,铁皮的面积是多少平方厘米?
20.学校要粉刷一间教室的四壁和天花。已知教室的长是9米,宽7米,高是3米,扣除门窗的面积12.5平方米,要粉刷的面积是多少平方米?如果每平方米需要花费4元涂料费,粉刷这个教室需要花费多少元?
