总复习 数与代数 第10课时《正比例与反比例》课件2023-2024学年六年级下册数学北师大版
文档属性
| 名称 | 总复习 数与代数 第10课时《正比例与反比例》课件2023-2024学年六年级下册数学北师大版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-22 10:27:47 | ||
图片预览





文档简介
(共25张PPT)
正比例与反比例
(总复习“数与代数”第10课时)
北师版·小学数学·六年级下册
01
什么是比?什么是比例?比的基本性质是?
两个数相除,叫作两个数的比。
满十进一!
两个比相等的式子叫作比例。
(一)回顾与交流
01
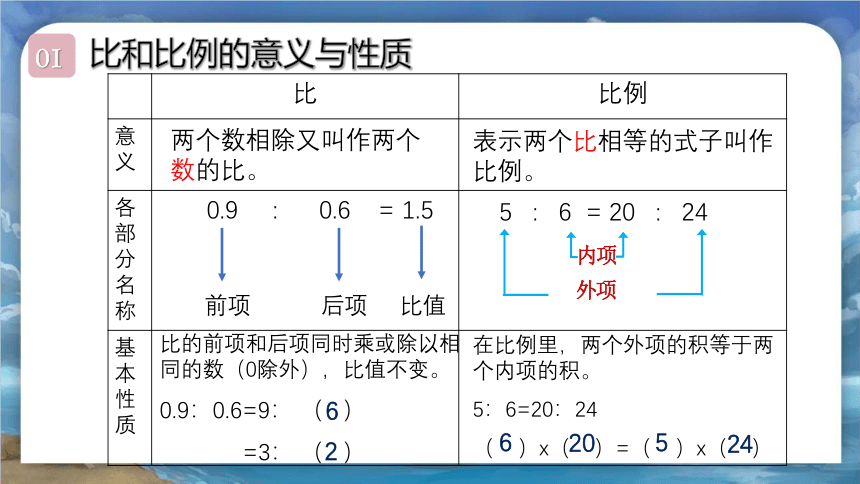
比和比例的意义与性质
比 比例
意义
各部分名称
基本性质
两个数相除又叫作两个数的比。
表示两个比相等的式子叫作比例。
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
0.9:0.6=9: ( )
=3: ( )
在比例里,两个外项的积等于两个内项的积。
5:6=20:24
( )x( )=( )x( )
0.9 : 0.6 = 1.5
前项 后项 比值
5 : 6 = 20 : 24
内项
外项
6
2
6
20
5
24
02
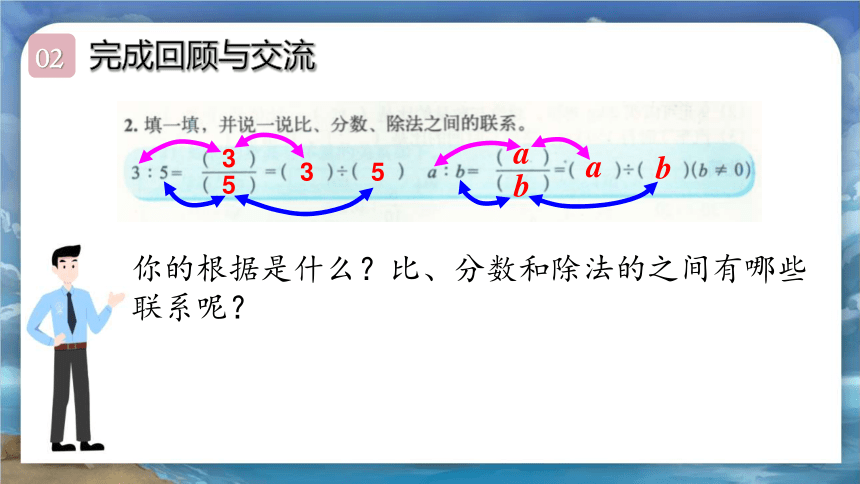
完成回顾与交流
3
5
3
5
a
b
a
b
你的根据是什么?比、分数和除法的之间有哪些联系呢?
02
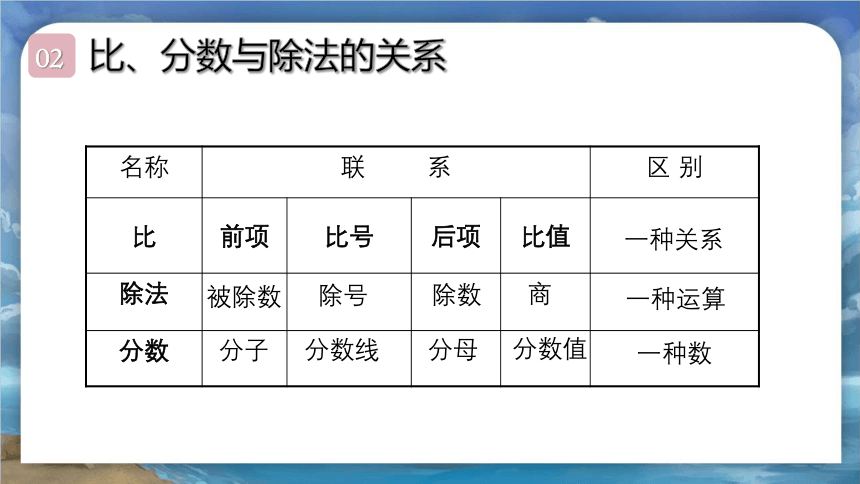
比、分数与除法的关系
名称 联 系 区 别
比 前项 比号 后项 比值
除法
分数
被除数
分子
除号
分数线
除数
分母
一种数
一种运算
一种关系
商
分数值
03
比例尺
图上距离和实际距离的比,叫作这幅图的比例尺。
图上距离∶实际距离 = 比例尺
分类
数值比例尺 如:1:10000000
线段比例尺 如:
(1)图上距离1cm表示实际距离6000cm,即是60m。
(2)240m=24000cm
24000× =4(cm)
(3)1÷ =
6000(cm)
=60(m)
3000(cm)
=30(m)
0.5÷ =
60×30=
1800(m2)
答:略。
3.(1)说说图中的比例尺1:6000表示什么意思。
(2)240m长的马路在图上应画多长?
(3)一个长方形住宅区在图上长1cm,宽0.5cm,它的实际占地面积是多少平方米?
04
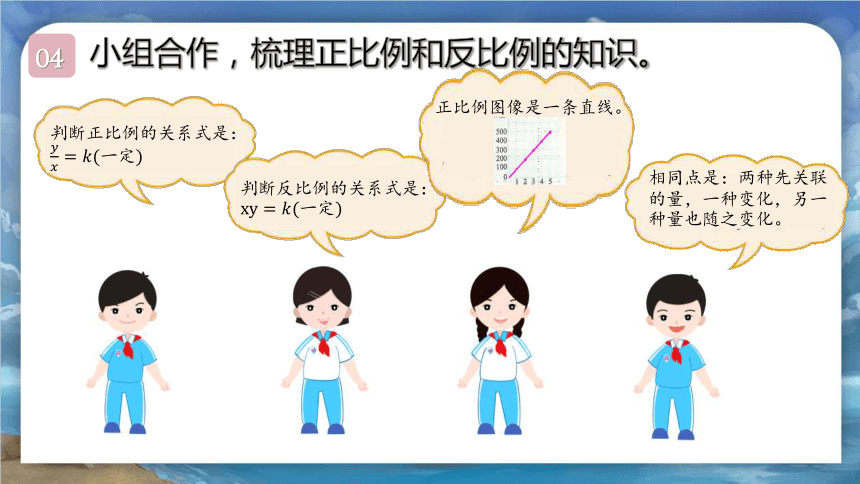
小组合作,梳理正比例和反比例的知识。
满十进一!
判断正比例的关系式是:
相同点是:两种先关联的量,一种变化,另一种量也随之变化。
满十进一!
判断反比例的关系式是:
正比例图像是一条直线。
04
正比例和反比例的区别与联系。
相同点 不同点 特征 关系式
正比例
反比例 两种相关联的量,一种量变化,另一种也随着变化。
一种量扩大(缩小),另一种量也随着扩大(缩小)
两种量的比值一定
一种量扩大(缩小),另一种量反而缩小(扩大)
两种量的积一定
=k(一定)
×
=k(一定)
200
300
400
500
5.一辆在高速路上行驶,速度保持在100千米/时。说一说汽车行驶的路程随时间变化的情况,并用多种方式表达这两个量之间的关系。
(1)可以列表。
(2)可以画图。
(3)可以用式子表示。
如果用t表示汽车行驶的时间,s表示汽车行驶的路程,那么 ___________________ 。
(4)判断路程与时间是否成正比例,说说你是怎么想的。
时间/时 1 2 3 4 5 …
路程/km 100 …
S÷t =
100
答:
路程与时间成正比例。
因为路程随着时间的变化而变化,而且路程与
时间的比值是相等,都是100。
(4)判断路程与时间是否成正比例,说说你是怎么想的。
1.填一填。
(1)两个正方形的边长比是1∶3,周长比是( ),面积比是( ) 。
(2)9元可以买2kg鸡蛋,总价与数量的比是( ) ,比值是( )。
(3)汽车3时行150 km,路程与时间的比是( ),比值是( )。
1∶3
1∶9
9∶2
4.5
150∶3
50
【选自教材P84巩固与应用第1题】
(二)巩固与应用
2.化简。
1∶4
4∶3
6∶1
1∶15
5∶12
5∶32
30∶1
1∶2
【选自教材P84巩固与应用第2题】
3.
(1)量一量艺术小学平面图的长是______cm,宽是______cm,这所小学实际占地面积是__________m2。
(2)绕操场跑一圈大约是______m,花坛的占地面积是______m2。
(3)教学楼的占地面积是______m2,是学校占地面积的_____%。
14
5
28000
240
1256
4200
15
【选自教材P84巩固与应用第3题】
4.解方程。
解: 4x=5
x=8
解: 0.5x=4
x=
解: 2x=2.5×2.8
x=3.5
【选自教材P84巩固与应用第4题】
5.判断下面每题中的两个量是否成正比例或反比例。
(1)一捆100 m长的电线,用去的长度与剩下的长度。
(2)三角形的面积一定,它的底和高。
(3)一个数与它的倒数。
不成比例
成反比例
成反比例
【选自教材P84巩固与应用第5题】
6.下面表格中的两个量是否成正比例或反比例?为什么?
每分滴数/滴 60 50 40 30 …
时间/分 20 24 30 40 …
每分滴数与所需时间成反比例。
60×20=1200,
50×24=1200;
40×30=1200,
30×40=1200;
【选自教材P85巩固与应用第6题】
(2)妙想的身高与体重的关系如下:
身高/厘米 100 110 120 130 …
体重/千克 17 20 25 31 …
妙想的身高与体重不成比例。
100×17=1700,
110×20=2200;
120÷25=4.8,
130÷31≈4.19。
(3)体积一定,圆柱体的底面积和高的关系如下。
底面积/ 平方分米 300 200 150 120 100 …
高/分米 2 3 4 5 6 …
体积一定,圆柱体的底面积和高成反比例。
300×2=600,
200×3=600,
150×4=600,
120×5=600,
7.磁悬浮列车匀速行驶时,路程与时间的关系如下。
时间/分 1 2 3 4 5 6 …
路程/km 7 14 21 28 35 42 …
(1)图中的点A表示时间为1分时,磁悬浮列车驶过的路程为7km。请你试着描出其他各点。
【选自教材P85巩固与应用第7题】
时间/分
路程/km
0
2
4
3
5
1
7
35
14
28
21
42
6
7
A
(2)连接各点,它们在一条直线上吗?
时间/分
路程/km
0
2
4
3
5
1
7
35
14
28
21
42
6
7
A
(3)列车运行2.5分时,行驶的路程是多少?
7×2.5=17.5(千米)
时间/分
路程/km
0
2
4
3
5
1
7
35
14
28
21
42
6
7
A
8.育才小学六年级同学从学校出发,乘车0.5时,来到离学校5km的科技馆,参观1时,出馆后休息0.5时,然后乘车0.5时返回学校。下面三幅图中,哪幅图描述了他们的这一活动行程呢?选一选。
√
【选自教材P85巩固与应用第8题】
(三)课堂总结
通过本节课的学习,你有哪些收获?
我学会了正比例、反比例的区别与联系。
满十进一!
我找到了比、除法、分数的联系。
正比例与反比例
(总复习“数与代数”第10课时)
北师版·小学数学·六年级下册
01
什么是比?什么是比例?比的基本性质是?
两个数相除,叫作两个数的比。
满十进一!
两个比相等的式子叫作比例。
(一)回顾与交流
01
比和比例的意义与性质
比 比例
意义
各部分名称
基本性质
两个数相除又叫作两个数的比。
表示两个比相等的式子叫作比例。
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
0.9:0.6=9: ( )
=3: ( )
在比例里,两个外项的积等于两个内项的积。
5:6=20:24
( )x( )=( )x( )
0.9 : 0.6 = 1.5
前项 后项 比值
5 : 6 = 20 : 24
内项
外项
6
2
6
20
5
24
02
完成回顾与交流
3
5
3
5
a
b
a
b
你的根据是什么?比、分数和除法的之间有哪些联系呢?
02
比、分数与除法的关系
名称 联 系 区 别
比 前项 比号 后项 比值
除法
分数
被除数
分子
除号
分数线
除数
分母
一种数
一种运算
一种关系
商
分数值
03
比例尺
图上距离和实际距离的比,叫作这幅图的比例尺。
图上距离∶实际距离 = 比例尺
分类
数值比例尺 如:1:10000000
线段比例尺 如:
(1)图上距离1cm表示实际距离6000cm,即是60m。
(2)240m=24000cm
24000× =4(cm)
(3)1÷ =
6000(cm)
=60(m)
3000(cm)
=30(m)
0.5÷ =
60×30=
1800(m2)
答:略。
3.(1)说说图中的比例尺1:6000表示什么意思。
(2)240m长的马路在图上应画多长?
(3)一个长方形住宅区在图上长1cm,宽0.5cm,它的实际占地面积是多少平方米?
04
小组合作,梳理正比例和反比例的知识。
满十进一!
判断正比例的关系式是:
相同点是:两种先关联的量,一种变化,另一种量也随之变化。
满十进一!
判断反比例的关系式是:
正比例图像是一条直线。
04
正比例和反比例的区别与联系。
相同点 不同点 特征 关系式
正比例
反比例 两种相关联的量,一种量变化,另一种也随着变化。
一种量扩大(缩小),另一种量也随着扩大(缩小)
两种量的比值一定
一种量扩大(缩小),另一种量反而缩小(扩大)
两种量的积一定
=k(一定)
×
=k(一定)
200
300
400
500
5.一辆在高速路上行驶,速度保持在100千米/时。说一说汽车行驶的路程随时间变化的情况,并用多种方式表达这两个量之间的关系。
(1)可以列表。
(2)可以画图。
(3)可以用式子表示。
如果用t表示汽车行驶的时间,s表示汽车行驶的路程,那么 ___________________ 。
(4)判断路程与时间是否成正比例,说说你是怎么想的。
时间/时 1 2 3 4 5 …
路程/km 100 …
S÷t =
100
答:
路程与时间成正比例。
因为路程随着时间的变化而变化,而且路程与
时间的比值是相等,都是100。
(4)判断路程与时间是否成正比例,说说你是怎么想的。
1.填一填。
(1)两个正方形的边长比是1∶3,周长比是( ),面积比是( ) 。
(2)9元可以买2kg鸡蛋,总价与数量的比是( ) ,比值是( )。
(3)汽车3时行150 km,路程与时间的比是( ),比值是( )。
1∶3
1∶9
9∶2
4.5
150∶3
50
【选自教材P84巩固与应用第1题】
(二)巩固与应用
2.化简。
1∶4
4∶3
6∶1
1∶15
5∶12
5∶32
30∶1
1∶2
【选自教材P84巩固与应用第2题】
3.
(1)量一量艺术小学平面图的长是______cm,宽是______cm,这所小学实际占地面积是__________m2。
(2)绕操场跑一圈大约是______m,花坛的占地面积是______m2。
(3)教学楼的占地面积是______m2,是学校占地面积的_____%。
14
5
28000
240
1256
4200
15
【选自教材P84巩固与应用第3题】
4.解方程。
解: 4x=5
x=8
解: 0.5x=4
x=
解: 2x=2.5×2.8
x=3.5
【选自教材P84巩固与应用第4题】
5.判断下面每题中的两个量是否成正比例或反比例。
(1)一捆100 m长的电线,用去的长度与剩下的长度。
(2)三角形的面积一定,它的底和高。
(3)一个数与它的倒数。
不成比例
成反比例
成反比例
【选自教材P84巩固与应用第5题】
6.下面表格中的两个量是否成正比例或反比例?为什么?
每分滴数/滴 60 50 40 30 …
时间/分 20 24 30 40 …
每分滴数与所需时间成反比例。
60×20=1200,
50×24=1200;
40×30=1200,
30×40=1200;
【选自教材P85巩固与应用第6题】
(2)妙想的身高与体重的关系如下:
身高/厘米 100 110 120 130 …
体重/千克 17 20 25 31 …
妙想的身高与体重不成比例。
100×17=1700,
110×20=2200;
120÷25=4.8,
130÷31≈4.19。
(3)体积一定,圆柱体的底面积和高的关系如下。
底面积/ 平方分米 300 200 150 120 100 …
高/分米 2 3 4 5 6 …
体积一定,圆柱体的底面积和高成反比例。
300×2=600,
200×3=600,
150×4=600,
120×5=600,
7.磁悬浮列车匀速行驶时,路程与时间的关系如下。
时间/分 1 2 3 4 5 6 …
路程/km 7 14 21 28 35 42 …
(1)图中的点A表示时间为1分时,磁悬浮列车驶过的路程为7km。请你试着描出其他各点。
【选自教材P85巩固与应用第7题】
时间/分
路程/km
0
2
4
3
5
1
7
35
14
28
21
42
6
7
A
(2)连接各点,它们在一条直线上吗?
时间/分
路程/km
0
2
4
3
5
1
7
35
14
28
21
42
6
7
A
(3)列车运行2.5分时,行驶的路程是多少?
7×2.5=17.5(千米)
时间/分
路程/km
0
2
4
3
5
1
7
35
14
28
21
42
6
7
A
8.育才小学六年级同学从学校出发,乘车0.5时,来到离学校5km的科技馆,参观1时,出馆后休息0.5时,然后乘车0.5时返回学校。下面三幅图中,哪幅图描述了他们的这一活动行程呢?选一选。
√
【选自教材P85巩固与应用第8题】
(三)课堂总结
通过本节课的学习,你有哪些收获?
我学会了正比例、反比例的区别与联系。
满十进一!
我找到了比、除法、分数的联系。
