3.10 探索图形课件(共39张PPT)2023-2024学年五年级下册数学人教版
文档属性
| 名称 | 3.10 探索图形课件(共39张PPT)2023-2024学年五年级下册数学人教版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-22 00:00:00 | ||
图片预览






文档简介
(共39张PPT)
探 索 图 形
人教版五年级下册
教学目标
通过操作、观察,使学生发现小正方体涂色情况的位置特征和规律,加深对正方体特征的认识和理解。
在解决问题的过程中,体会分类、数形结合、归纳、推理、模型的数学思想,培养实事求是的科学态度。
通过操作、观察、演示、想象等活动,获得“化繁为简”的经验,培养学生动手能力和空间想象能力。
练习导入
填 一 填
正方体有( )个面,( )条棱,( )个顶点。
6
12
8
.
面
棱
顶点
新知导入
探 索 图 形
新知讲解
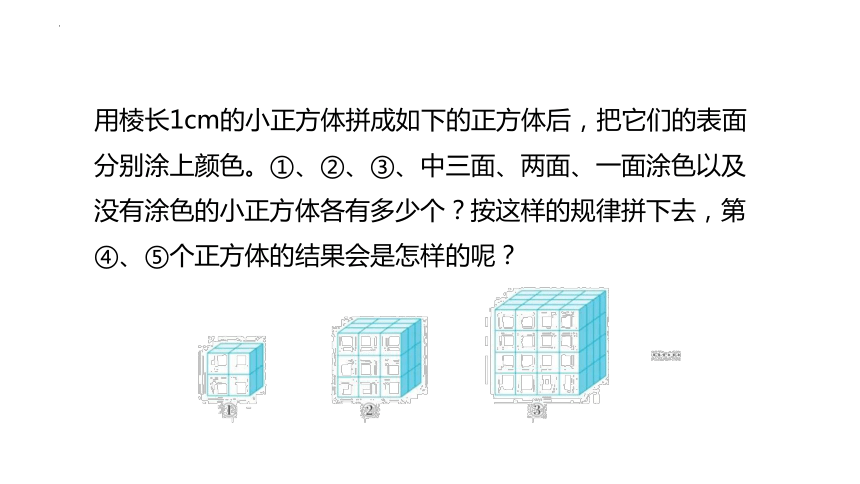
用棱长1cm的小正方体拼成如下的正方体后,把它们的表面分别涂上颜色。①、②、③、中三面、两面、一面涂色以及没有涂色的小正方体各有多少个?按这样的规律拼下去,第④、⑤个正方体的结果会是怎样的呢?
新知讲解
完成下表。看看每类小正方体都在什么位置。你能发现什么规律?
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
①
②
③
④
⑤
新知讲解
要求:
1、用小正方体图形摆出相应的图形。
2、观察每类小正方体都在什么位置。
3、把结果填写在记录表中。
4、观察记录的数据,找到规律。
小组合作学习
新知讲解
展 示 汇 报
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
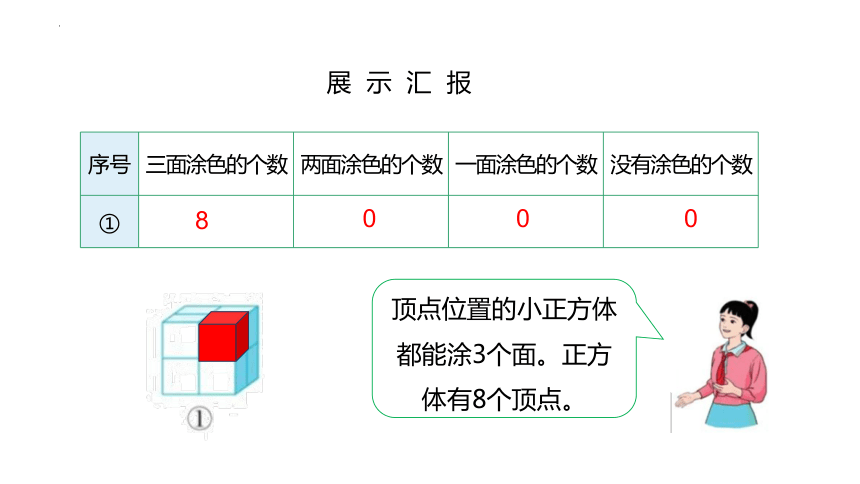
①
顶点位置的小正方体都能涂3个面。正方体有8个顶点。
8
0 0 0
新知讲解
展 示 汇 报
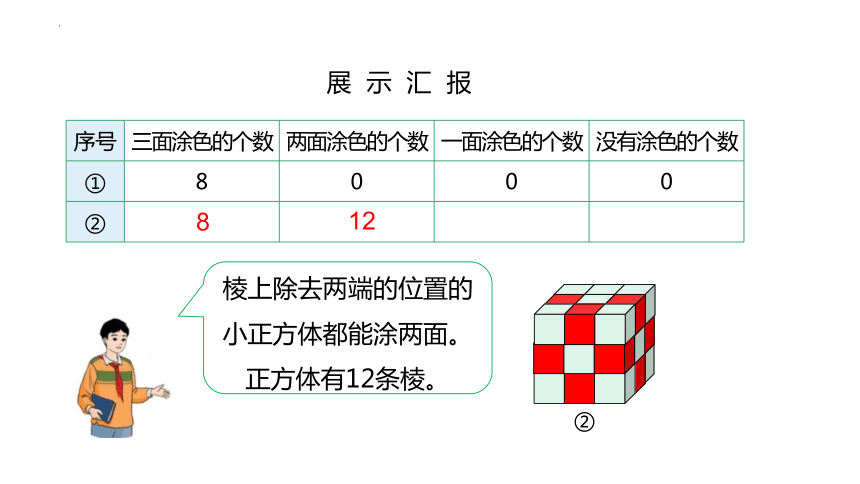
棱上除去两端的位置的小正方体都能涂两面。正方体有12条棱。
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
① 8 0 0 0
②
8
12
②
新知讲解
展 示 汇 报
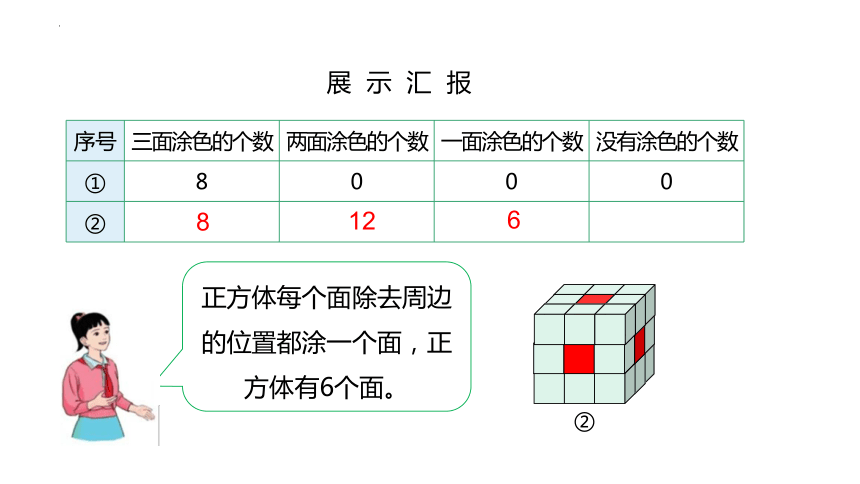
正方体每个面除去周边的位置都涂一个面,正方体有6个面。
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
① 8 0 0 0
②
8
12
6
②
新知讲解
展 示 汇 报
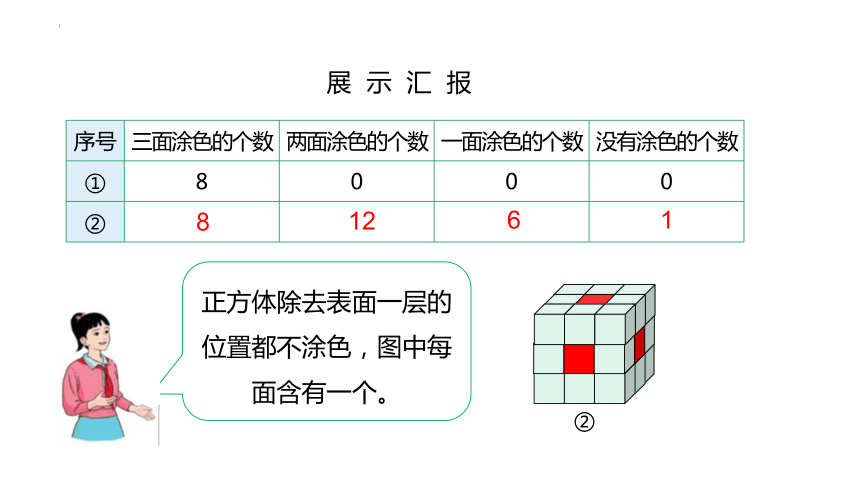
正方体除去表面一层的位置都不涂色,图中每面含有一个。
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
① 8 0 0 0
②
8
12
6
1
②
新知讲解
展 示 汇 报
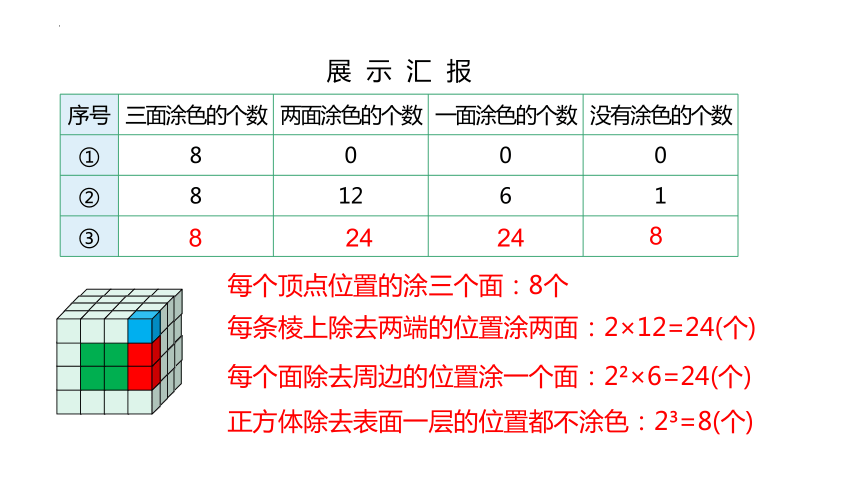
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
① 8 0 0 0
② 8 12 6 1
③
每个顶点位置的涂三个面:8个
8
每条棱上除去两端的位置涂两面:2×12=24(个)
24
每个面除去周边的位置涂一个面:2 ×6=24(个)
24
正方体除去表面一层的位置都不涂色:2 =8(个)
8
新知讲解
猜 想 验 证
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
① 8 0 0 0
② 8 12 6 1
③ 8 24 24 8
④
按这样的规律摆下去,你能猜出第④个大正方体的结果吗?
三个面:8个
8
两个面:(5-2)×12=36(个)
36
一个面:(5-2) ×6=54(个)
54
没有涂:(5-2) =27(个)
27
新知讲解
猜 想 验 证
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
① 8 0 0 0
② 8 12 6 1
③ 8 24 24 8
④ 8 36 54 27
⑤
猜出第⑤个大正方体的结果吗?
三面涂色:8个
两面涂色:(6-2)×12=48(个)
一面涂色:(6-2) ×6=54(个)
没有涂色:(6-2) =27(个)
8
48
96
64
新知讲解
说一说:你发现了什么规律?
(每条棱上小正方体的个数为n)。
三面涂色:8个
两面涂色:(n-2)×12
一面涂色:(n-2) ×6
没有涂色:(n-2)
新知讲解
记忆口诀
8个顶点涂三面,
12棱长中间两面涂,
6面中心涂一面,
没有涂色在正中心。
新知讲解
1)你能继续写出第⑥⑦⑧个正方体中四类小正方体的个数吗?
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
① 8 0 0 0
② 8 12 6 1
③ 8 24 24 8
④ 8 36 54 27
⑤ 8 48 96 64
⑥
⑦
⑧
8 60 150 125
8 72 216 216
8 84 294 343
新知讲解
2)如何摆出下面的几何体,你会数吗?
新知讲解
要求:
1、用小正方体图形摆出相应的图形。
2、观察每一层的各数。
3、计算每个图形的正方体的个数。
4、找到数图形个数的规律。
小组合作学习
第一层
第二层
一 共
新课讲解
展 示 汇 报
1+(1+2)=4(个)
1 个
1+2=3(个)
第一层
第二层
第三层
一 共
新知讲解
1+2+3=6(个)
1 个
1+2=3(个)
1+(1+2)+(1+2+3)=10(个)
展 示 汇 报
第一层
第二层
第三层
第四层
一 共
新知讲解
1+2+3=6(个)
1 个
1+2=3(个)
1+(1+2)+(1+2+3)+(1+2+3+4)=20(个)
展 示 汇 报
1+2+3+4=10(个)
新知讲解
按这个规律摆下去,第五个图形的结果是多少?第n个图形呢?
1+(1+2)+(1+2+3)+(1+2+3+4)+(1+2+3+4+5) +(1+2+3+4+5+6)=56(个)
第五个图形有6层:
新知讲解
1+(1+2)+(1+2+3)+(1+2+3+4)+……+
(1+2+3+4+…… +n+1)
第n个图形有(n+1)层:
课堂练习------基础题
1、把表面为绿色的正方体的棱平均分为4份,然后沿等分线把正方体切开,得到( )个角正方体。
1)三面涂色的小正方体有( )个。
2)两面涂色的小正方体有( )个。
3)只有一面涂色的小正方体有( )个。
64
8
24
24
如图都是由3层没有缝隙的小正方体组成的几何体,如果它的外表面(包括底面)全都被涂成绿色,那么把它们在分成一个一个的小正方体时,有( )个小正方体恰好是三个面是绿色的。
课堂练习------基础题
2、一把钥匙开一把锁。
C
A 12 B 14 C 16
把14个棱长为一厘米的小正方体在地面上堆叠成如右图所示的形状,然后将露在外面的部分涂成红色,底面不涂,那么涂红色部分的面积为( )平方厘米。
课堂练习------基础题
C
A 21 B 24 C 33
作业布置------基础题
3、把表面涂色的正方体每条棱平均分成10份儿,从切成的小正方体中任取一个,三面涂色、二面涂色、一面涂色的小正方体各有多少个?
三面涂色:8个
二面涂色:(10-2)×12=96(个)
一面涂色: (10-2) ×6=384(个)
答:三面涂色的8个,二面涂色的96个,一面涂色的384个。
课堂练习------提高题
4、一个正方体,在它的每个面都涂上蓝色,再把它切成棱长是1厘米的角正方体。已知两面涂色的小正方体有48个,大正方体的棱长是几厘米?
每条棱上有小正方体:
48÷12+2=6(个)
1×6=6(厘米)
答:大正方体的棱长是6厘米。
课堂练习------拓展题
5、一个长方体木块如图,长5厘米,宽4厘米,高3厘米,现在把它的6个面上都涂上颜色,然后把它锯成棱长都是1厘米的小正方体。木块中三面涂色的有多少块?两面涂色的有多少块?六面都没有涂色的有多少块?
三面涂色:8块
两面涂色:(3+2+1)×4=24(块)
没有涂色:3×2×1=6(块)
答:三面涂色的8块,两面涂色的24块,没有涂色的6块。
课堂总结
说一说:
通过刚才的学习,你有什么收获?
知道了小正方体涂色情况的位置特征和规律。
学会了计算“塔”型排列的正方体的规律。
板书设计
探索图形
三面涂色:8个
两面涂色:(n-2)×12
一面涂色:(n-2) ×6
没有涂色:(n-2)
作业布置
要认真完成呦!
作业布置------知识技能类
1、你能数出下面的几何体中各有多少个小正方体吗?
( ) ( ) ( )
20个
29个
39个
作业布置------知识技能类
2、下图是由64个小正方体拼成的一个大正方体,把它的表面全部涂色。
(1)3面涂色的一共有( )个。
(2)2面涂色的一共有12×( )=( )个。
(3)1面涂色的一共有6×( )=( )个。
(4)用64个小正方体-( )个涂色的小正方体=( )
个没有涂色的小正方体。
8
2
24
2
24
58
8
作业布置------知识技能类
3、右图是由( )个棱长为1厘米的 正方体搭成的。将这个立体图形的表面涂上蓝色(底面不涂),其中只有三个面涂上蓝色的正方体有( )个,只有四个面涂上蓝色正方体有( )个。
5
1
3
4、一个正方体,在它的每个面上都涂上红色,再把它切成棱长是1厘米的小正方体。已知两面涂色的小正方体有96个,大正方体的体积是多少立方厘米?
作业布置------知识技能类
96÷12+2=10(个)
10×1=10(厘米)
10×10×10=1000(立方厘米)
答:原来大正方体的体积是1000立方厘米。
作业布置------选做题
5、先把下图的几何体表面涂色后,再在下表中填写小正方体涂色面个数的情况。(底面也涂)
涂色面数/个 1 2 3 4 5
正方体个数
1
5
6
3
1
作业布置------综合实践类
6、找一个魔方,计算涂一面、两面、三面的小正方体的个数。
探 索 图 形
人教版五年级下册
教学目标
通过操作、观察,使学生发现小正方体涂色情况的位置特征和规律,加深对正方体特征的认识和理解。
在解决问题的过程中,体会分类、数形结合、归纳、推理、模型的数学思想,培养实事求是的科学态度。
通过操作、观察、演示、想象等活动,获得“化繁为简”的经验,培养学生动手能力和空间想象能力。
练习导入
填 一 填
正方体有( )个面,( )条棱,( )个顶点。
6
12
8
.
面
棱
顶点
新知导入
探 索 图 形
新知讲解
用棱长1cm的小正方体拼成如下的正方体后,把它们的表面分别涂上颜色。①、②、③、中三面、两面、一面涂色以及没有涂色的小正方体各有多少个?按这样的规律拼下去,第④、⑤个正方体的结果会是怎样的呢?
新知讲解
完成下表。看看每类小正方体都在什么位置。你能发现什么规律?
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
①
②
③
④
⑤
新知讲解
要求:
1、用小正方体图形摆出相应的图形。
2、观察每类小正方体都在什么位置。
3、把结果填写在记录表中。
4、观察记录的数据,找到规律。
小组合作学习
新知讲解
展 示 汇 报
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
①
顶点位置的小正方体都能涂3个面。正方体有8个顶点。
8
0 0 0
新知讲解
展 示 汇 报
棱上除去两端的位置的小正方体都能涂两面。正方体有12条棱。
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
① 8 0 0 0
②
8
12
②
新知讲解
展 示 汇 报
正方体每个面除去周边的位置都涂一个面,正方体有6个面。
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
① 8 0 0 0
②
8
12
6
②
新知讲解
展 示 汇 报
正方体除去表面一层的位置都不涂色,图中每面含有一个。
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
① 8 0 0 0
②
8
12
6
1
②
新知讲解
展 示 汇 报
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
① 8 0 0 0
② 8 12 6 1
③
每个顶点位置的涂三个面:8个
8
每条棱上除去两端的位置涂两面:2×12=24(个)
24
每个面除去周边的位置涂一个面:2 ×6=24(个)
24
正方体除去表面一层的位置都不涂色:2 =8(个)
8
新知讲解
猜 想 验 证
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
① 8 0 0 0
② 8 12 6 1
③ 8 24 24 8
④
按这样的规律摆下去,你能猜出第④个大正方体的结果吗?
三个面:8个
8
两个面:(5-2)×12=36(个)
36
一个面:(5-2) ×6=54(个)
54
没有涂:(5-2) =27(个)
27
新知讲解
猜 想 验 证
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
① 8 0 0 0
② 8 12 6 1
③ 8 24 24 8
④ 8 36 54 27
⑤
猜出第⑤个大正方体的结果吗?
三面涂色:8个
两面涂色:(6-2)×12=48(个)
一面涂色:(6-2) ×6=54(个)
没有涂色:(6-2) =27(个)
8
48
96
64
新知讲解
说一说:你发现了什么规律?
(每条棱上小正方体的个数为n)。
三面涂色:8个
两面涂色:(n-2)×12
一面涂色:(n-2) ×6
没有涂色:(n-2)
新知讲解
记忆口诀
8个顶点涂三面,
12棱长中间两面涂,
6面中心涂一面,
没有涂色在正中心。
新知讲解
1)你能继续写出第⑥⑦⑧个正方体中四类小正方体的个数吗?
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
① 8 0 0 0
② 8 12 6 1
③ 8 24 24 8
④ 8 36 54 27
⑤ 8 48 96 64
⑥
⑦
⑧
8 60 150 125
8 72 216 216
8 84 294 343
新知讲解
2)如何摆出下面的几何体,你会数吗?
新知讲解
要求:
1、用小正方体图形摆出相应的图形。
2、观察每一层的各数。
3、计算每个图形的正方体的个数。
4、找到数图形个数的规律。
小组合作学习
第一层
第二层
一 共
新课讲解
展 示 汇 报
1+(1+2)=4(个)
1 个
1+2=3(个)
第一层
第二层
第三层
一 共
新知讲解
1+2+3=6(个)
1 个
1+2=3(个)
1+(1+2)+(1+2+3)=10(个)
展 示 汇 报
第一层
第二层
第三层
第四层
一 共
新知讲解
1+2+3=6(个)
1 个
1+2=3(个)
1+(1+2)+(1+2+3)+(1+2+3+4)=20(个)
展 示 汇 报
1+2+3+4=10(个)
新知讲解
按这个规律摆下去,第五个图形的结果是多少?第n个图形呢?
1+(1+2)+(1+2+3)+(1+2+3+4)+(1+2+3+4+5) +(1+2+3+4+5+6)=56(个)
第五个图形有6层:
新知讲解
1+(1+2)+(1+2+3)+(1+2+3+4)+……+
(1+2+3+4+…… +n+1)
第n个图形有(n+1)层:
课堂练习------基础题
1、把表面为绿色的正方体的棱平均分为4份,然后沿等分线把正方体切开,得到( )个角正方体。
1)三面涂色的小正方体有( )个。
2)两面涂色的小正方体有( )个。
3)只有一面涂色的小正方体有( )个。
64
8
24
24
如图都是由3层没有缝隙的小正方体组成的几何体,如果它的外表面(包括底面)全都被涂成绿色,那么把它们在分成一个一个的小正方体时,有( )个小正方体恰好是三个面是绿色的。
课堂练习------基础题
2、一把钥匙开一把锁。
C
A 12 B 14 C 16
把14个棱长为一厘米的小正方体在地面上堆叠成如右图所示的形状,然后将露在外面的部分涂成红色,底面不涂,那么涂红色部分的面积为( )平方厘米。
课堂练习------基础题
C
A 21 B 24 C 33
作业布置------基础题
3、把表面涂色的正方体每条棱平均分成10份儿,从切成的小正方体中任取一个,三面涂色、二面涂色、一面涂色的小正方体各有多少个?
三面涂色:8个
二面涂色:(10-2)×12=96(个)
一面涂色: (10-2) ×6=384(个)
答:三面涂色的8个,二面涂色的96个,一面涂色的384个。
课堂练习------提高题
4、一个正方体,在它的每个面都涂上蓝色,再把它切成棱长是1厘米的角正方体。已知两面涂色的小正方体有48个,大正方体的棱长是几厘米?
每条棱上有小正方体:
48÷12+2=6(个)
1×6=6(厘米)
答:大正方体的棱长是6厘米。
课堂练习------拓展题
5、一个长方体木块如图,长5厘米,宽4厘米,高3厘米,现在把它的6个面上都涂上颜色,然后把它锯成棱长都是1厘米的小正方体。木块中三面涂色的有多少块?两面涂色的有多少块?六面都没有涂色的有多少块?
三面涂色:8块
两面涂色:(3+2+1)×4=24(块)
没有涂色:3×2×1=6(块)
答:三面涂色的8块,两面涂色的24块,没有涂色的6块。
课堂总结
说一说:
通过刚才的学习,你有什么收获?
知道了小正方体涂色情况的位置特征和规律。
学会了计算“塔”型排列的正方体的规律。
板书设计
探索图形
三面涂色:8个
两面涂色:(n-2)×12
一面涂色:(n-2) ×6
没有涂色:(n-2)
作业布置
要认真完成呦!
作业布置------知识技能类
1、你能数出下面的几何体中各有多少个小正方体吗?
( ) ( ) ( )
20个
29个
39个
作业布置------知识技能类
2、下图是由64个小正方体拼成的一个大正方体,把它的表面全部涂色。
(1)3面涂色的一共有( )个。
(2)2面涂色的一共有12×( )=( )个。
(3)1面涂色的一共有6×( )=( )个。
(4)用64个小正方体-( )个涂色的小正方体=( )
个没有涂色的小正方体。
8
2
24
2
24
58
8
作业布置------知识技能类
3、右图是由( )个棱长为1厘米的 正方体搭成的。将这个立体图形的表面涂上蓝色(底面不涂),其中只有三个面涂上蓝色的正方体有( )个,只有四个面涂上蓝色正方体有( )个。
5
1
3
4、一个正方体,在它的每个面上都涂上红色,再把它切成棱长是1厘米的小正方体。已知两面涂色的小正方体有96个,大正方体的体积是多少立方厘米?
作业布置------知识技能类
96÷12+2=10(个)
10×1=10(厘米)
10×10×10=1000(立方厘米)
答:原来大正方体的体积是1000立方厘米。
作业布置------选做题
5、先把下图的几何体表面涂色后,再在下表中填写小正方体涂色面个数的情况。(底面也涂)
涂色面数/个 1 2 3 4 5
正方体个数
1
5
6
3
1
作业布置------综合实践类
6、找一个魔方,计算涂一面、两面、三面的小正方体的个数。
