第四单元:分数的意义和性质单元复习课件(共45张PPT)人教版五年级数学下册
文档属性
| 名称 | 第四单元:分数的意义和性质单元复习课件(共45张PPT)人教版五年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-22 11:02:07 | ||
图片预览









文档简介
(共45张PPT)
分数的意义和性质复习专题
人教版五年级数学下册
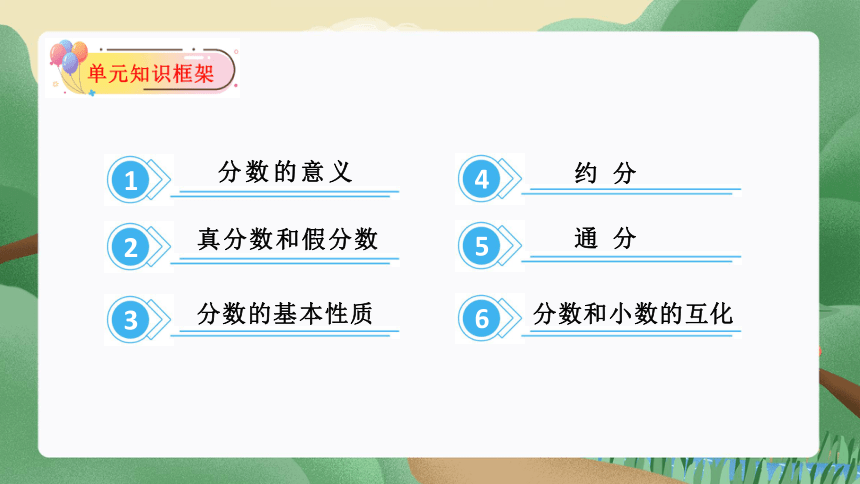
1
分数的意义
2
真分数和假分数
3
分数的基本性质
4
约分
5
通分
6
分数和小数的互化
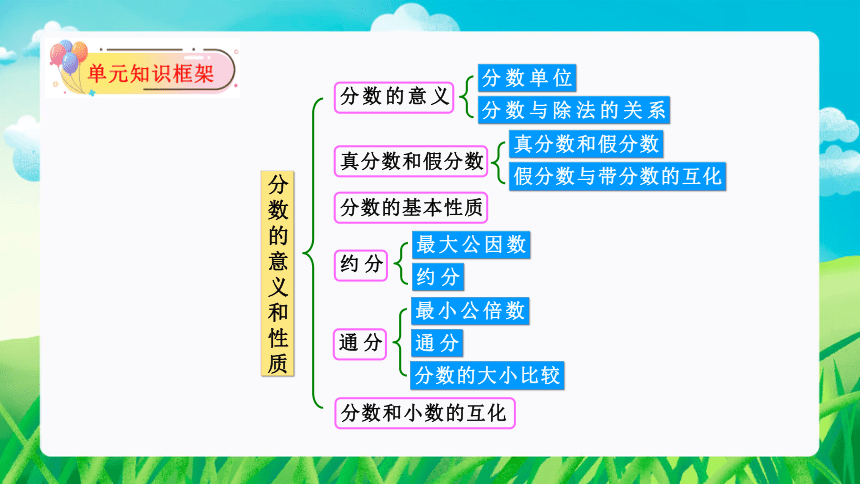
分数的意义和性质
分数的意义
分数单位
分数与除法的关系
真分数和假分数
真分数和假分数
假分数与带分数的互化
分数的基本性质
约分
最大公因数
约分
通分
最小公倍数
通分
分数的大小比较
分数和小数的互化
1
分数的意义
1、分数的意义:把单位“1”平均分成若干份,表示这样的一份或几份的数,叫做分数。
2、分数单位:把单位“1”平均分成若干份,表示这样的一份的数叫做分数单位。
3、分数与除法的关系:除法中的被除数相当于分数的分子,除数相等于分母,分数线相当于除号。
被除数÷除数= ,用字母表示:a÷b= (b≠0)。
【例1】乐乐看一本书,已经看了,是把( )看作单位“1”,平均分成( )份,已看的占( )份。
把谁平均分,就把谁看作单位“1”。
这本书的总页数
分成若干份是指分成除0以外的任意整数份,分时一定是平均分,只有平均分才可用分数来表示。
5
3
【例2】读作( ),它的分数单位是( ),它有( )个这样的分数单位,再加上( )个这样的分数单位就得到1。
把单位“1”平均分成9份,所以分数单位是。
有7个这样的分数单位;
和1相差2个,所以再加上2个这样的分数单位就得到1。
九分之七
7
2
2
真分数和假分数
分数的分类:
1、真分数:分子比分母小的分数叫做真分数。
2、假分数:分子比分母大或者分子和分母相等的分数,叫做假分数。
真分数小于1。
假分数大于或等于1。
任何整数(0除外)都可以化成分母是1的假分数。
3、带分数:由整数(0除外)和真分数合成的数叫做带分数。
(1)带分数的读法:
先读带分数的整数部分,再读分数部分,分数部分和整数部分中间加一个“又”字。
(2)带分数的写法:
“又”前面是整数部分,后面是分数部分,先写整数部分,再写分数部分。
带分数大于1。
【例3】若分数(m是自然数)是真分数,m最大可以是( );若是假分数,m最小可以是( );当m=( )时, 等于0。
当是真分数时,m<12,因为m是自然数,所以m最大是11;
当是假分数时,m≥12,因为m是自然数,所以最小是12;
当m等于0时, =0;
11
12
0
【例4】分子是5的假分数有( )个。
A、6 B、5 C、4 D、3
分子比分母大或者分子和分母相等的分数,叫做假分数。分子是5的假分数有 , , , , 共5个。
B
任何整数(0除外)都可以化成分母是1的假分数。
(1)把假分数化成整数或带分数的方法:
用分子除以分母,能整除的,所得商就是整数;不能整除的,商就是带分数的整数部分,余数就是分数部分的分子,分母不变。
(2)把带分数化成假分数的方法:
用整数部分乘以分母再加上分子作为这个分数的分子,分母不变。
假分数与带分数的互化
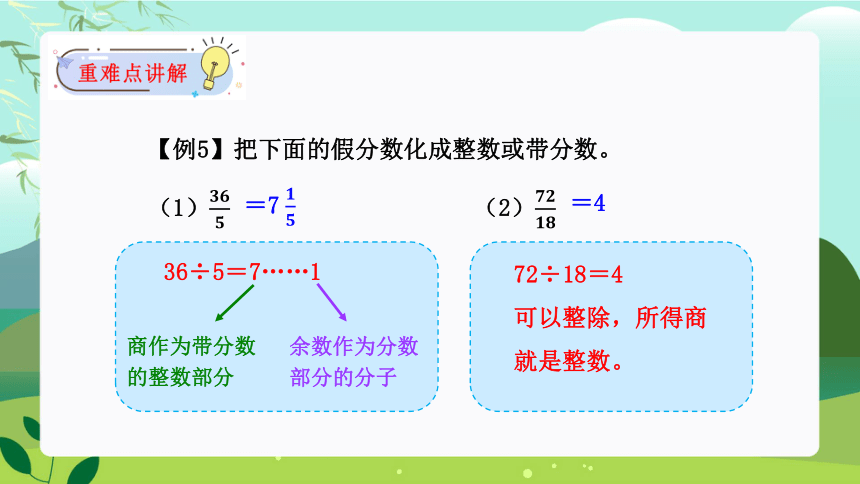
【例5】把下面的假分数化成整数或带分数。
(1) (2)
36÷5=7……1
商作为带分数的整数部分
余数作为分数部分的分子
=7
72÷18=4
可以整除,所得商就是整数。
=4
【例5】把下面的假分数化成整数或带分数。
(3)
(4)
(5)
(6)
=8
=3
=5
=11
(3)53÷6=8……5
(4)39÷13=3
(5)27÷5=5……2
(6)80÷7=11……3
【例6】有一个带分数,它的分数部分的分子是6,把它化成假分数后分子是13,则这个带分数是( )。
1
将带分数化成假分数,用整数部分乘上带分数的分母再加上分子作为假分数的分子,假分数的分母不变。13-6=7,即带分数的整数部分与分母的积为7。因为7=1×7,因此,这个带分数的整数部分为1,分母为7。
【例7】如图,把一个六边形看作单位“1”,则图中阴影部分用分数表示是( ),它的分数单位是( ),将这个分数化成带分数是( )
如图把一个六边形看作单位“1”,每个六边形平均分成6份,阴影部分占了11份,所以阴影部分用表示。
的分数单位是;
化成带分数是1。
1
3
分数的基本性质
1、分数的基本性质
分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变,这叫做分数的基本性质。
分母不同而大小不变的分数,也可以把一个分数化成指定分母的分数。
分数的基本性质与除法中商不变的规律类似,要注意不为0的条件。
【例8】填空:= = ( )÷( )。
21
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
= = ;
= = ;
=7÷8;
40
7
8
【例9】如果将的分子扩大到原来的5倍,要使分数大小不变,分母应该加上( )。
30
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。将 的分子扩大到原来的5倍,要使分数的大小不变,分母也应该扩大到原来的5倍,则分母应该加上:6×5-6=30。故要使分数的大小不变,分母应该加上30;
【例10】如果将的分子加上12,要使分数大小不变,分母应该加上( )。
A、12 B、27 C、36
B
将 的分子加上12,则分子为4+12=16,即分子扩大到原来的4倍。要使分数的大小不变,分母也应该扩大到原来的4倍,则分母应该加上:9×4-9=27。故要使分数的大小不变,分母应该加上27,选B。
4
约分
1、最大公因数
几个数公有的因数,叫作这几个数的公因数。
其中最大的那个叫作这几个数的最大公因数。
2、互质数:公因数只有1的两个数叫做互质数。
3、求两个数最大公因数的方法
(1)列举法:先分别找出两个数的因数,从中找出公因数,再找出公因数中最大的那个;
(2)筛选法:先找出两个数中较小数的因数,从中圈出另一个数的因数,再看哪一个最大;
(3)分解质因数法:先把每个数都写成几个质因数相乘的形式,再从这些质因数中找出这两个数公有的质因数,这些公有的质因数的乘积就是这两个数的最大公因数;
(4)短除法:先把这两个数公有的质因数按从小到大的顺序依次作除数,连续去除这两个数,直到得出的两个商只有公因数1为止,再把所有的除数相乘,所得的积就是这两个数的最大公因数。
【例11】找出下面每组数的最大公因数。
(1)12和18 (2)14和21
12 18
2
6
9
12和18的最大公因数是2×3=6
3
2
3
14 21
7
2
3
14和21的最大公因数是7
最大公因数
【例12】体育老师把15个呼啦圈和20根跳绳平均分给几个小组,正好可以分完。最多可以分给多少个小组?
【分析】根据题意,最多能分的小组数是15和20的最大公因数,用分解质因数法求出这两个数的最大公因数即可。
15=5×3
20=5×2×2
所以,15和20的最大公因数是5。
答:最多可分给5个小组。
【例13】一间会议室长5米,宽3米,用边长为( )分米整块的正方形地砖刚好可以铺满。
A、4 B、5 C、6 D、7
由题意可知,正方形地砖的边长是会议室的长和宽的公因数。
5米=50分米,3米=30分米。
50 30
2
25
15
5
5
3
5是50和30的公因数,故选B。
B
1、约分
把一个分数化成和它相等,但分子和分母都比较小的分数,叫做约分。
约分依据的是分数的基本性质。
2、分子和分母只有公因数1的分数是最简分数。
约分时,通常要约成最简分数。
约分
【例14】将下列分数进行约分。
(1)
(2)
(3)
(4)
==
==
==
==
根据分数的基本性质,可以将分数约分成最简分数。将分子和分母同时除以它们的最大公因数即可得到最简分数。最简分数的分子和分母互质。
【例15】有一个最简真分数,分子和分母的和是11,这样的分数有( )个。
最简真分数是指分子小于分母,且分子和分母没有公共因数的分数。11=1+10=2+9=3+8=4+7=5+6,所以可以组成最简分数为:,,,,共5个。
5
【例16】一堆煤共100千克,第一次用去了26千克,第二次用去了34千克,两次一共用去了煤的总量几分之几?
第一次用的质量加上第二次用的质量,再除以煤的总量
(26+34)÷100
=60÷100
=
=
答:两次一共用去了煤的总量五分之三。
1、最小公倍数
几个数共有的倍数叫做它们的公倍数,其中最小的一个叫最小公倍数。
2、求两个数最小公倍数的方法
(1)列举法:先分别找出两个数的倍数,从中找出公倍数,再找出最小的那个;
(2)筛选法:先找出两个数中较大数的倍数,从中圈出另一个数的倍数,再看哪一个最小;
5
通分
(3)分解质因数法:把每个数都写成几个质因数相乘的形式,其中相同的质因数与各自独有质因数的乘积就是这两个数的最小公倍数;
(4)短除法:先把这两个数公有的质因数按从小到大的顺序依次作除数,连续去除这两个数,直到得出的两个商只有公因数1为止,再把所有的除数和最后所得的商连乘,所得的积就是它们的最小公倍数。
【例17】找出下面每组数的最小公倍数。
(1)30和45 (2)28和49
30 45
5
6
9
30和45的最小公倍数是
5×3×2×3=90
3
2
3
28 49
7
4
7
28和49的最小公倍数是
7×4×7=196
最小公倍数
【例18】饲养员给小熊猫分竹笋,无论是分给12只小熊猫,还是分给16只小熊猫,都能正好分完。饲养员至少有多少根竹笋?
【分析】根据题意,竹笋的根数是12和16的最小公倍数,用分解质因数法求出这两个数的最小公倍数即可。
12=3×2×2
15=5×3
所以,12和15的最小公倍数为:3×2×5×2=60
答:饲养员至少有60根竹笋。
1、通分的意义
把异分母分数分别化成和原来分数相等的同分母分数,叫做通分。
2、通分的方法
通分时用原分母的公倍数作公分母,为了计算简便,通常选用它们的最小公倍数作公分母,然后把各分数化成用这个最小公倍数作分母的分数。
通分
【例19】将下列分数进行通分。
(1)和 (2)和 (3)和
(1)同分母的两个分数,分子大的分数就大,分子小的分数就小;
(2)同分子的两个分数,分母大的分数反而小,分母小的分数反而大。
(3)异分母的两个分数,先化成同分母分数(分数单位相同),再进行比较。
分数的大小比较
【例20】墩墩和岗岗比赛做计算题,墩墩2分钟做了15道,岗岗3分钟做了20道,墩墩和岗岗谁做题的速度更快?
题数÷时间=做题速度
墩墩:15÷2= (道)
岗岗:20÷3= (道)
= , = ,
>
答:墩墩做题的速度更快。
【例21】商店购进了同样多的苹果、梨和橙子,卖出一部分后,苹果还剩,梨还剩橙子还剩,哪种水果卖得最好?
因为三种水果原来一样多,所以直接比较三个分数的大小,分数最小的表示剩下的最少也就是卖出的最多。
苹果:= = ,
梨:= = ,
橙子:= = ,
>>
答:苹果卖得最好。
6
分数和小数的互化
分数化成小数的方法:
1、分母是10,100,1000……的分数化成小数,可以直接去掉分母,看分母中有几个0,有几个0就在分子中从右边起向左数出几位,点上小数点;
2、分母不是10,100,1000……的分数化成小数,用分子除以分母,除不尽时,要根据需要按“四舍五入”法保留几位小数。
3、把带分数化成小数,方法与上面相同,带分数的整数部分作为小数的整数部分,分数部分化成小数,作为小数的小数部分。
【例22】下面的分数化成小数,(除不尽的保留两位小数)。
(1)
(2)
(3)1
(4)
=3.5
=0.8
=1.375
≈0.42
(1)7÷2=3.5
(2)4÷5=0.8
(3)3÷8=0.375,0.375+1=1.375
(4)5÷12≈0.42
分数化成小数
小数化成分数的方法:
1、一位小数化分数,用10作分母,一位小数去掉小数点作分子;
2、两位小数化分数,用100作分母,两位小数去掉小数点作分子……,其余多位小数的,以此类推。
3、把小数化成分数,能约分的都应约成最简分数。
小数化成分数
【例23】下面的小数化成分数。
(1)0.28
(2)1.3
(3)2.5
(4)0.125
=
=
=
=
(1)0.28= =
(2)1.3=
(3)2.5= =
(4)0.125= =
1、把一瓶3升的牛奶倒满5个同样大小的杯子后,正好倒完。每杯刚好占这瓶牛奶的,是升,相当于1升的。
2、16和20的最小公倍数是( )。
5
1
5
3
5
3
80
3、辩一辩,对的打√,错的打×。
(1)米既可以表示1米的,也可以表示3米的。( )
(2) > 。( )
(3)1里面有5个, 有12个。( )
√
×
×
4、把一根8米长的木料,平均分成5段,每段占全长的几分之几?每段长多少米?
1÷5=
8÷5= (米)
答:每段占全长的,每段长米。
每一份努力,都将在学习中得到最好的回报。加油!
分数的意义和性质复习专题
人教版五年级数学下册
1
分数的意义
2
真分数和假分数
3
分数的基本性质
4
约分
5
通分
6
分数和小数的互化
分数的意义和性质
分数的意义
分数单位
分数与除法的关系
真分数和假分数
真分数和假分数
假分数与带分数的互化
分数的基本性质
约分
最大公因数
约分
通分
最小公倍数
通分
分数的大小比较
分数和小数的互化
1
分数的意义
1、分数的意义:把单位“1”平均分成若干份,表示这样的一份或几份的数,叫做分数。
2、分数单位:把单位“1”平均分成若干份,表示这样的一份的数叫做分数单位。
3、分数与除法的关系:除法中的被除数相当于分数的分子,除数相等于分母,分数线相当于除号。
被除数÷除数= ,用字母表示:a÷b= (b≠0)。
【例1】乐乐看一本书,已经看了,是把( )看作单位“1”,平均分成( )份,已看的占( )份。
把谁平均分,就把谁看作单位“1”。
这本书的总页数
分成若干份是指分成除0以外的任意整数份,分时一定是平均分,只有平均分才可用分数来表示。
5
3
【例2】读作( ),它的分数单位是( ),它有( )个这样的分数单位,再加上( )个这样的分数单位就得到1。
把单位“1”平均分成9份,所以分数单位是。
有7个这样的分数单位;
和1相差2个,所以再加上2个这样的分数单位就得到1。
九分之七
7
2
2
真分数和假分数
分数的分类:
1、真分数:分子比分母小的分数叫做真分数。
2、假分数:分子比分母大或者分子和分母相等的分数,叫做假分数。
真分数小于1。
假分数大于或等于1。
任何整数(0除外)都可以化成分母是1的假分数。
3、带分数:由整数(0除外)和真分数合成的数叫做带分数。
(1)带分数的读法:
先读带分数的整数部分,再读分数部分,分数部分和整数部分中间加一个“又”字。
(2)带分数的写法:
“又”前面是整数部分,后面是分数部分,先写整数部分,再写分数部分。
带分数大于1。
【例3】若分数(m是自然数)是真分数,m最大可以是( );若是假分数,m最小可以是( );当m=( )时, 等于0。
当是真分数时,m<12,因为m是自然数,所以m最大是11;
当是假分数时,m≥12,因为m是自然数,所以最小是12;
当m等于0时, =0;
11
12
0
【例4】分子是5的假分数有( )个。
A、6 B、5 C、4 D、3
分子比分母大或者分子和分母相等的分数,叫做假分数。分子是5的假分数有 , , , , 共5个。
B
任何整数(0除外)都可以化成分母是1的假分数。
(1)把假分数化成整数或带分数的方法:
用分子除以分母,能整除的,所得商就是整数;不能整除的,商就是带分数的整数部分,余数就是分数部分的分子,分母不变。
(2)把带分数化成假分数的方法:
用整数部分乘以分母再加上分子作为这个分数的分子,分母不变。
假分数与带分数的互化
【例5】把下面的假分数化成整数或带分数。
(1) (2)
36÷5=7……1
商作为带分数的整数部分
余数作为分数部分的分子
=7
72÷18=4
可以整除,所得商就是整数。
=4
【例5】把下面的假分数化成整数或带分数。
(3)
(4)
(5)
(6)
=8
=3
=5
=11
(3)53÷6=8……5
(4)39÷13=3
(5)27÷5=5……2
(6)80÷7=11……3
【例6】有一个带分数,它的分数部分的分子是6,把它化成假分数后分子是13,则这个带分数是( )。
1
将带分数化成假分数,用整数部分乘上带分数的分母再加上分子作为假分数的分子,假分数的分母不变。13-6=7,即带分数的整数部分与分母的积为7。因为7=1×7,因此,这个带分数的整数部分为1,分母为7。
【例7】如图,把一个六边形看作单位“1”,则图中阴影部分用分数表示是( ),它的分数单位是( ),将这个分数化成带分数是( )
如图把一个六边形看作单位“1”,每个六边形平均分成6份,阴影部分占了11份,所以阴影部分用表示。
的分数单位是;
化成带分数是1。
1
3
分数的基本性质
1、分数的基本性质
分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变,这叫做分数的基本性质。
分母不同而大小不变的分数,也可以把一个分数化成指定分母的分数。
分数的基本性质与除法中商不变的规律类似,要注意不为0的条件。
【例8】填空:= = ( )÷( )。
21
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
= = ;
= = ;
=7÷8;
40
7
8
【例9】如果将的分子扩大到原来的5倍,要使分数大小不变,分母应该加上( )。
30
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。将 的分子扩大到原来的5倍,要使分数的大小不变,分母也应该扩大到原来的5倍,则分母应该加上:6×5-6=30。故要使分数的大小不变,分母应该加上30;
【例10】如果将的分子加上12,要使分数大小不变,分母应该加上( )。
A、12 B、27 C、36
B
将 的分子加上12,则分子为4+12=16,即分子扩大到原来的4倍。要使分数的大小不变,分母也应该扩大到原来的4倍,则分母应该加上:9×4-9=27。故要使分数的大小不变,分母应该加上27,选B。
4
约分
1、最大公因数
几个数公有的因数,叫作这几个数的公因数。
其中最大的那个叫作这几个数的最大公因数。
2、互质数:公因数只有1的两个数叫做互质数。
3、求两个数最大公因数的方法
(1)列举法:先分别找出两个数的因数,从中找出公因数,再找出公因数中最大的那个;
(2)筛选法:先找出两个数中较小数的因数,从中圈出另一个数的因数,再看哪一个最大;
(3)分解质因数法:先把每个数都写成几个质因数相乘的形式,再从这些质因数中找出这两个数公有的质因数,这些公有的质因数的乘积就是这两个数的最大公因数;
(4)短除法:先把这两个数公有的质因数按从小到大的顺序依次作除数,连续去除这两个数,直到得出的两个商只有公因数1为止,再把所有的除数相乘,所得的积就是这两个数的最大公因数。
【例11】找出下面每组数的最大公因数。
(1)12和18 (2)14和21
12 18
2
6
9
12和18的最大公因数是2×3=6
3
2
3
14 21
7
2
3
14和21的最大公因数是7
最大公因数
【例12】体育老师把15个呼啦圈和20根跳绳平均分给几个小组,正好可以分完。最多可以分给多少个小组?
【分析】根据题意,最多能分的小组数是15和20的最大公因数,用分解质因数法求出这两个数的最大公因数即可。
15=5×3
20=5×2×2
所以,15和20的最大公因数是5。
答:最多可分给5个小组。
【例13】一间会议室长5米,宽3米,用边长为( )分米整块的正方形地砖刚好可以铺满。
A、4 B、5 C、6 D、7
由题意可知,正方形地砖的边长是会议室的长和宽的公因数。
5米=50分米,3米=30分米。
50 30
2
25
15
5
5
3
5是50和30的公因数,故选B。
B
1、约分
把一个分数化成和它相等,但分子和分母都比较小的分数,叫做约分。
约分依据的是分数的基本性质。
2、分子和分母只有公因数1的分数是最简分数。
约分时,通常要约成最简分数。
约分
【例14】将下列分数进行约分。
(1)
(2)
(3)
(4)
==
==
==
==
根据分数的基本性质,可以将分数约分成最简分数。将分子和分母同时除以它们的最大公因数即可得到最简分数。最简分数的分子和分母互质。
【例15】有一个最简真分数,分子和分母的和是11,这样的分数有( )个。
最简真分数是指分子小于分母,且分子和分母没有公共因数的分数。11=1+10=2+9=3+8=4+7=5+6,所以可以组成最简分数为:,,,,共5个。
5
【例16】一堆煤共100千克,第一次用去了26千克,第二次用去了34千克,两次一共用去了煤的总量几分之几?
第一次用的质量加上第二次用的质量,再除以煤的总量
(26+34)÷100
=60÷100
=
=
答:两次一共用去了煤的总量五分之三。
1、最小公倍数
几个数共有的倍数叫做它们的公倍数,其中最小的一个叫最小公倍数。
2、求两个数最小公倍数的方法
(1)列举法:先分别找出两个数的倍数,从中找出公倍数,再找出最小的那个;
(2)筛选法:先找出两个数中较大数的倍数,从中圈出另一个数的倍数,再看哪一个最小;
5
通分
(3)分解质因数法:把每个数都写成几个质因数相乘的形式,其中相同的质因数与各自独有质因数的乘积就是这两个数的最小公倍数;
(4)短除法:先把这两个数公有的质因数按从小到大的顺序依次作除数,连续去除这两个数,直到得出的两个商只有公因数1为止,再把所有的除数和最后所得的商连乘,所得的积就是它们的最小公倍数。
【例17】找出下面每组数的最小公倍数。
(1)30和45 (2)28和49
30 45
5
6
9
30和45的最小公倍数是
5×3×2×3=90
3
2
3
28 49
7
4
7
28和49的最小公倍数是
7×4×7=196
最小公倍数
【例18】饲养员给小熊猫分竹笋,无论是分给12只小熊猫,还是分给16只小熊猫,都能正好分完。饲养员至少有多少根竹笋?
【分析】根据题意,竹笋的根数是12和16的最小公倍数,用分解质因数法求出这两个数的最小公倍数即可。
12=3×2×2
15=5×3
所以,12和15的最小公倍数为:3×2×5×2=60
答:饲养员至少有60根竹笋。
1、通分的意义
把异分母分数分别化成和原来分数相等的同分母分数,叫做通分。
2、通分的方法
通分时用原分母的公倍数作公分母,为了计算简便,通常选用它们的最小公倍数作公分母,然后把各分数化成用这个最小公倍数作分母的分数。
通分
【例19】将下列分数进行通分。
(1)和 (2)和 (3)和
(1)同分母的两个分数,分子大的分数就大,分子小的分数就小;
(2)同分子的两个分数,分母大的分数反而小,分母小的分数反而大。
(3)异分母的两个分数,先化成同分母分数(分数单位相同),再进行比较。
分数的大小比较
【例20】墩墩和岗岗比赛做计算题,墩墩2分钟做了15道,岗岗3分钟做了20道,墩墩和岗岗谁做题的速度更快?
题数÷时间=做题速度
墩墩:15÷2= (道)
岗岗:20÷3= (道)
= , = ,
>
答:墩墩做题的速度更快。
【例21】商店购进了同样多的苹果、梨和橙子,卖出一部分后,苹果还剩,梨还剩橙子还剩,哪种水果卖得最好?
因为三种水果原来一样多,所以直接比较三个分数的大小,分数最小的表示剩下的最少也就是卖出的最多。
苹果:= = ,
梨:= = ,
橙子:= = ,
>>
答:苹果卖得最好。
6
分数和小数的互化
分数化成小数的方法:
1、分母是10,100,1000……的分数化成小数,可以直接去掉分母,看分母中有几个0,有几个0就在分子中从右边起向左数出几位,点上小数点;
2、分母不是10,100,1000……的分数化成小数,用分子除以分母,除不尽时,要根据需要按“四舍五入”法保留几位小数。
3、把带分数化成小数,方法与上面相同,带分数的整数部分作为小数的整数部分,分数部分化成小数,作为小数的小数部分。
【例22】下面的分数化成小数,(除不尽的保留两位小数)。
(1)
(2)
(3)1
(4)
=3.5
=0.8
=1.375
≈0.42
(1)7÷2=3.5
(2)4÷5=0.8
(3)3÷8=0.375,0.375+1=1.375
(4)5÷12≈0.42
分数化成小数
小数化成分数的方法:
1、一位小数化分数,用10作分母,一位小数去掉小数点作分子;
2、两位小数化分数,用100作分母,两位小数去掉小数点作分子……,其余多位小数的,以此类推。
3、把小数化成分数,能约分的都应约成最简分数。
小数化成分数
【例23】下面的小数化成分数。
(1)0.28
(2)1.3
(3)2.5
(4)0.125
=
=
=
=
(1)0.28= =
(2)1.3=
(3)2.5= =
(4)0.125= =
1、把一瓶3升的牛奶倒满5个同样大小的杯子后,正好倒完。每杯刚好占这瓶牛奶的,是升,相当于1升的。
2、16和20的最小公倍数是( )。
5
1
5
3
5
3
80
3、辩一辩,对的打√,错的打×。
(1)米既可以表示1米的,也可以表示3米的。( )
(2) > 。( )
(3)1里面有5个, 有12个。( )
√
×
×
4、把一根8米长的木料,平均分成5段,每段占全长的几分之几?每段长多少米?
1÷5=
8÷5= (米)
答:每段占全长的,每段长米。
每一份努力,都将在学习中得到最好的回报。加油!
