5.3 平行线的性质 课件(共19张PPT)-人教版数学七年级下册
文档属性
| 名称 | 5.3 平行线的性质 课件(共19张PPT)-人教版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-25 07:08:25 | ||
图片预览





文档简介
(共19张PPT)
人教版七年级下册
5.3平行线的性质
文字叙述 符号语言 图形
相等 两直线平行 ∴a∥b
相等 两直线平行 ∴a∥b 互补 两直线平行 ∴a∥b 同位角
内错角
同旁内角
∵∠1=∠2
∵∠2+∠4=180°
a
b
c
1
2
3
4
1.平行线的判定
温故知新
∵∠2=∠3
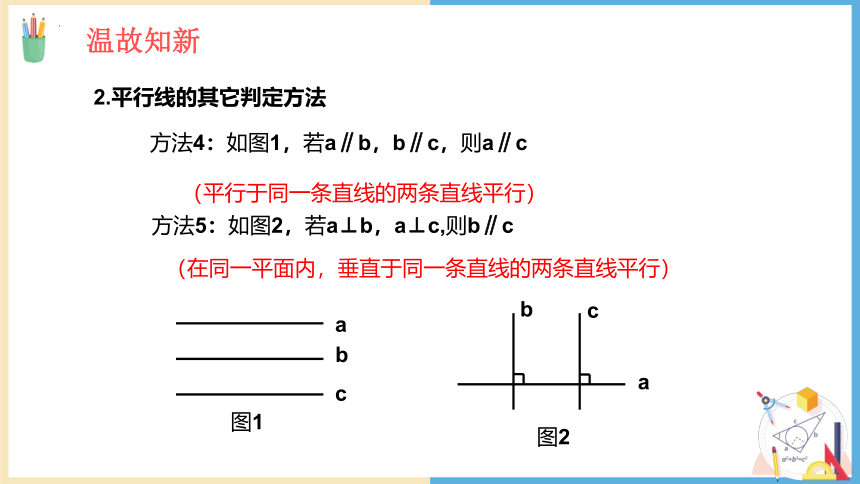
2.平行线的其它判定方法
a
b
c
图1
a
b
c
图2
温故知新
方法4:如图1,若a∥b,b∥c,则a∥c
(平行于同一条直线的两条直线平行)
方法5:如图2,若a⊥b,a⊥c,则b∥c
(在同一平面内,垂直于同一条直线的两条直线平行)
动手量一量
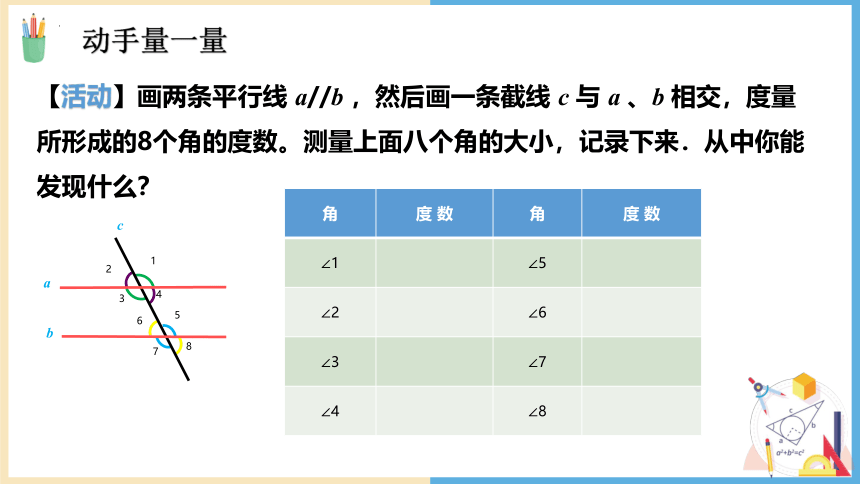
【活动】画两条平行线 a//b ,然后画一条截线 c 与 a 、b 相交,度量所形成的8个角的度数。测量上面八个角的大小,记录下来.从中你能发现什么?
a
b
c
1
2
3
4
5
6
7
8
角 度 数 角 度 数
∠1 ∠5
∠2 ∠6
∠3 ∠7
∠4 ∠8
探究新知
我们可以猜想:
如果两条平行线被第三条直线所截,
同位角 。
相等
探究新知
【性质1】两条平行线被第三条直线所截,同位角相等。
两直线平行,同位角相等。
a
b
c
1
2
∵ a // b(已知)
∠1=∠2 ( 两直线平行,同位角相等 )
几何语言
几何画板演示
平行线会影响内错角和同旁内角吗?图中的∠1和∠2是什么关系呢?
思考1
解:
内错角
∵ a // b(已知)
∠1=∠3 ( 两直线平行,同位角相等 )
∵ ∠2=∠3 ( 对顶角相等 )
∠1=∠2 ( 两直线平行,内错角相等 )
探究新知
【性质2】两条平行线被第三条直线所截,内错角相等。
两直线平行,内错角相等。
∵ a // b(已知)
∠1=∠2 ( 两直线平行,内错角相等 )
几何语言
a
b
c
1
2
几何画板演示
已知 a // b ,∠1=80°,∠2 =?
夹在平行线间的同旁内角
A. 80° B.100° C.无法判定
思考2
解:
∵ a // b(已知)
∠1=∠3 ( 两直线平行,内错角相等 )
又∵ ∠1=80° ,∠3=80°
∠2=180°-∠3=100°( 两直线平行,同旁内角互补)
√
探究新知
【性质3】两条平行线被第三条直线所截,同旁内角互补。
两直线平行,同旁内角互补。
a
b
c
1
2
∵ a // b(已知)
∠1+∠2=180°
( 两直线平行,同旁内角互补 )
几何语言
几何画板演示
试一试
【典例2】如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?
A
B
C
D
解:
因为梯形上、下底互相平行,
所以A与∠D互补, ∠B与∠C互补.
∴ ∠C=180° - ∠B = 180° - 115°=65° .
∴ ∠D=180° - ∠A = 180° - 100°=80° .
练一练
1. 如图,直线a // b, ∠1=54°,∠2 , ∠3, ∠4 各是多少
解: ∵a // b(已知)
∠1=∠2=54°(对顶角相等)
又∵∠1=54°
∠2+∠3=180°(两直线平行,同旁内角互补)
∠3=126°
∠4=∠2=54°(两直线平行,内错角相等)
练一练
2.如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B = 60°,∠AED=40°.
(1) DE和BC平行吗?为什么?(2)∠C是多少度?为什么?
解:
(1)互相平行,理由如下:
∵ ∠ADE= ∠B = 60°
∴ DE∥ BC ( 同位角相等,两直线平行 )
A
B
C
E
D
(2)∠C =40°
∵DE∥ BC
∴ ∠C=∠AED ( 两直线平行,同位角相等 )
又∵ ∠AED=40°
∴ ∠C =∠AED =40°. ( 两直线平行,内错角相等 )
比一比
平行线的判定与性质有什么区别?
两直线平行
同位角相等
内错角相等
同旁内角互补
线的关系
角的关系
平行线的性质
平行线的判定
平行线的性质:
a
b
c
1
2
a
b
c
1
2
a
b
c
1
2
课堂小结
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
课后作业:
1.必做题:课本的对应习题
作业:
2.选做题:历届中考题
人教版七年级下册
5.3平行线的性质
文字叙述 符号语言 图形
相等 两直线平行 ∴a∥b
相等 两直线平行 ∴a∥b 互补 两直线平行 ∴a∥b 同位角
内错角
同旁内角
∵∠1=∠2
∵∠2+∠4=180°
a
b
c
1
2
3
4
1.平行线的判定
温故知新
∵∠2=∠3
2.平行线的其它判定方法
a
b
c
图1
a
b
c
图2
温故知新
方法4:如图1,若a∥b,b∥c,则a∥c
(平行于同一条直线的两条直线平行)
方法5:如图2,若a⊥b,a⊥c,则b∥c
(在同一平面内,垂直于同一条直线的两条直线平行)
动手量一量
【活动】画两条平行线 a//b ,然后画一条截线 c 与 a 、b 相交,度量所形成的8个角的度数。测量上面八个角的大小,记录下来.从中你能发现什么?
a
b
c
1
2
3
4
5
6
7
8
角 度 数 角 度 数
∠1 ∠5
∠2 ∠6
∠3 ∠7
∠4 ∠8
探究新知
我们可以猜想:
如果两条平行线被第三条直线所截,
同位角 。
相等
探究新知
【性质1】两条平行线被第三条直线所截,同位角相等。
两直线平行,同位角相等。
a
b
c
1
2
∵ a // b(已知)
∠1=∠2 ( 两直线平行,同位角相等 )
几何语言
几何画板演示
平行线会影响内错角和同旁内角吗?图中的∠1和∠2是什么关系呢?
思考1
解:
内错角
∵ a // b(已知)
∠1=∠3 ( 两直线平行,同位角相等 )
∵ ∠2=∠3 ( 对顶角相等 )
∠1=∠2 ( 两直线平行,内错角相等 )
探究新知
【性质2】两条平行线被第三条直线所截,内错角相等。
两直线平行,内错角相等。
∵ a // b(已知)
∠1=∠2 ( 两直线平行,内错角相等 )
几何语言
a
b
c
1
2
几何画板演示
已知 a // b ,∠1=80°,∠2 =?
夹在平行线间的同旁内角
A. 80° B.100° C.无法判定
思考2
解:
∵ a // b(已知)
∠1=∠3 ( 两直线平行,内错角相等 )
又∵ ∠1=80° ,∠3=80°
∠2=180°-∠3=100°( 两直线平行,同旁内角互补)
√
探究新知
【性质3】两条平行线被第三条直线所截,同旁内角互补。
两直线平行,同旁内角互补。
a
b
c
1
2
∵ a // b(已知)
∠1+∠2=180°
( 两直线平行,同旁内角互补 )
几何语言
几何画板演示
试一试
【典例2】如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?
A
B
C
D
解:
因为梯形上、下底互相平行,
所以A与∠D互补, ∠B与∠C互补.
∴ ∠C=180° - ∠B = 180° - 115°=65° .
∴ ∠D=180° - ∠A = 180° - 100°=80° .
练一练
1. 如图,直线a // b, ∠1=54°,∠2 , ∠3, ∠4 各是多少
解: ∵a // b(已知)
∠1=∠2=54°(对顶角相等)
又∵∠1=54°
∠2+∠3=180°(两直线平行,同旁内角互补)
∠3=126°
∠4=∠2=54°(两直线平行,内错角相等)
练一练
2.如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B = 60°,∠AED=40°.
(1) DE和BC平行吗?为什么?(2)∠C是多少度?为什么?
解:
(1)互相平行,理由如下:
∵ ∠ADE= ∠B = 60°
∴ DE∥ BC ( 同位角相等,两直线平行 )
A
B
C
E
D
(2)∠C =40°
∵DE∥ BC
∴ ∠C=∠AED ( 两直线平行,同位角相等 )
又∵ ∠AED=40°
∴ ∠C =∠AED =40°. ( 两直线平行,内错角相等 )
比一比
平行线的判定与性质有什么区别?
两直线平行
同位角相等
内错角相等
同旁内角互补
线的关系
角的关系
平行线的性质
平行线的判定
平行线的性质:
a
b
c
1
2
a
b
c
1
2
a
b
c
1
2
课堂小结
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
课后作业:
1.必做题:课本的对应习题
作业:
2.选做题:历届中考题
