8.2.2 消元加减法解二元一次方程组 课件-人教版七年级下册
文档属性
| 名称 | 8.2.2 消元加减法解二元一次方程组 课件-人教版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 426.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-25 11:01:25 | ||
图片预览








文档简介
(共20张PPT)
第八章二元一次方程组
人教版 七年级下册
8.2.2加减消元法解二元一次方程组
二、教学重点:
会用加减消元法解二元一次方程组。
三、教学难点:
掌握解二元一次方程组的“消元”思想。
学习目标
1、会用加减消元法解简单的二元一次方程组
2、理解解二元一次方程组的思路是“消元”,体会化归思想
重点:会用加减消元法解二元一次方程组。
难点:掌握解二元一次方程组的“消元”思想。
主要步骤:
基本思路:
写解
求解
代入
把变形后的方程代入到另一个方程中,消去一个元
分别求出两个未知数的值
写出方程组的解
变形
用含有一个未知数的代数式表示另一个未知数, 写成y=ax+b或x=ay+b
消元: 二元
1、解二元一次方程组的基本思路是什么?
2、用代入法解方程的步骤是什么?
一元
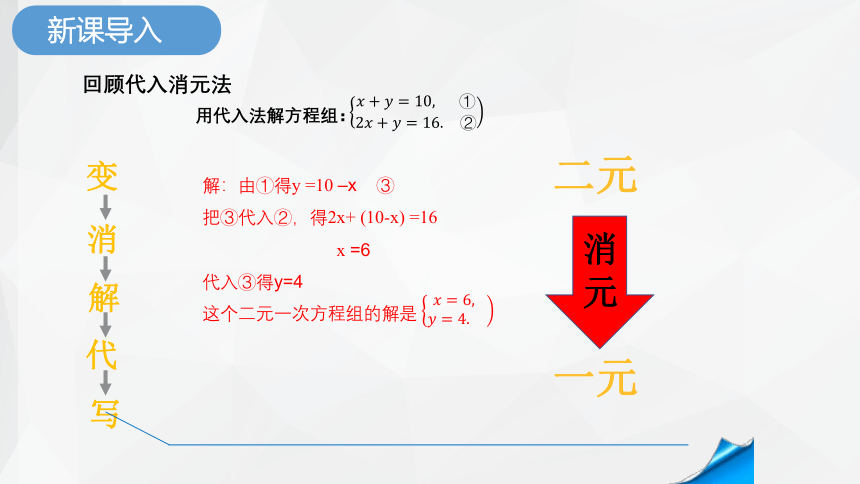
回顾代入消元法
新课导入
用代入法解方程组:
解:由①得y =10 –x ③
把③代入②,得2x+ (10-x) =16
x =6
代入③得y=4
这个二元一次方程组的解是
回顾代入消元法
新课导入
消
变
解
写
代
二元
一元
消元
观察方程组,这个方程组的两个方程中,y的系数有什么关系?
相等
利用这种关系能发现新的消元方法吗?
解: ②-①得2x-x=16-10
x=6
把x=6代入①得y=10-6=46
所以这个方程组得解是
用②-①可消去未知数y,化为一元一次方程.即(2x+y)-(x+y)=16-10
新课学习
用①-②也能消去未知数y,得(x+y)-(2x+y)=10-16
解:①-②得x-2x=10-16
-x=-6
x=6
把x=6代入①得y=4
所以这个方程组的解是
解二元一次方程组
新课学习
用加减法解方程组:
例1
导引:
两个方程中x的系数相同,y的系数互为相反数,
这样可以把两个方程相加消去y,或者把两个方
程相减消去x.
解:
此题中未知数的系数有什么新的关系?你能想到什么办法消元?
新课学习
方法一:①+②,得6x=12,解得x=2.把x=2
代入②,得3×2+7y=13,解得y=1.
所以原方程组的解为
方法二:①-②,得-14y=-14,解得y=1.
把y=1代入①,得3x-7×1=-1,解得x=2.
所以原方程组的解为
新课学习
加减法定义:当二元一次方程组的两个方程中同
一未知数的系数相反或相等时,把这两个方程的两边
分别相加或相减,就能消去这个未知数,得到一个一
元一次方程,这种方法叫做加减消元法,简称加减法.
新课学习
二元一次方程组
系数相同,相减消元
消元
加减
一元一次方程
转化
同一未知数
系数相反,相加消元
前提
新课学习
用加减法解方程组:
例2
在方程两边乘适当的数,变形成同一未知数在两个方程中的系数相反或相等.
直接加减是否可行?
不可行
怎样实现方程组中存在系数相同或相反的未知数,进而使用加减消元法呢?
新课学习
解:
①×3,得 9x+12y=48. ③
②×2,得 10x-12y=66. ④
③+④,得19x=114,
即 x=6.
把x=6代入① ,得 3×6+4y=16,
4y= -2,
y=
所以这个方程组的解是
新课学习
思考:对于一些系数不同或不互为相反数的二元一次方程组,还能用加减法来解吗
先变形,再加减消元
化归思想:将复杂问题通过变换转化为简单问题;将难解的问题通过变换转化为容易求解的问题;将未解决的问题通过变换转化为已解决的问题.这就是解决数学问题常用的化归思想.
新课学习
例3 解方程组:
导引:方程组中,两个方程中y的系数的绝对值成倍数
关系,方程②乘以3就可与方程①相加消去y.
解: 由②×3,得 51x-9y=222,③
由①+③,得 59x=295,解得 x=5.
把x=5代入①,得8×5+9y=73,解得
所以原方程组的解为
新课学习
1
2
3
思想:
消元
转化
解决
前提:
二元一次方程组的两个方程中同一未知数的系数相反或相等
步骤:
变形
加减
求解
回代
写解
二元
一元
用加减法消元法解二元一次方程组:
新课学习
课后练习
1、 用加减法解方程组:
①+②,得4x=8,
解这个方程,得x=2.
把x=2代入①,得y= .
因此,这个方程组的解是
解:
①×2,得10x+4y=50.③
③-②,得7x=35,解这个方程,得x=5.
把x=5代入①,得5×5+2y=25,y=0.
因此,这个方程组的解是
解:
用加减法解方程组 时,要使两个方程中同一未知数的系数相等或相反,有以下四种变形的结果:
其中变形正确的是( )
A.①② B.③④ C.①③ D.②④
B
2、
THANKS
第八章二元一次方程组
人教版 七年级下册
8.2.2加减消元法解二元一次方程组
二、教学重点:
会用加减消元法解二元一次方程组。
三、教学难点:
掌握解二元一次方程组的“消元”思想。
学习目标
1、会用加减消元法解简单的二元一次方程组
2、理解解二元一次方程组的思路是“消元”,体会化归思想
重点:会用加减消元法解二元一次方程组。
难点:掌握解二元一次方程组的“消元”思想。
主要步骤:
基本思路:
写解
求解
代入
把变形后的方程代入到另一个方程中,消去一个元
分别求出两个未知数的值
写出方程组的解
变形
用含有一个未知数的代数式表示另一个未知数, 写成y=ax+b或x=ay+b
消元: 二元
1、解二元一次方程组的基本思路是什么?
2、用代入法解方程的步骤是什么?
一元
回顾代入消元法
新课导入
用代入法解方程组:
解:由①得y =10 –x ③
把③代入②,得2x+ (10-x) =16
x =6
代入③得y=4
这个二元一次方程组的解是
回顾代入消元法
新课导入
消
变
解
写
代
二元
一元
消元
观察方程组,这个方程组的两个方程中,y的系数有什么关系?
相等
利用这种关系能发现新的消元方法吗?
解: ②-①得2x-x=16-10
x=6
把x=6代入①得y=10-6=46
所以这个方程组得解是
用②-①可消去未知数y,化为一元一次方程.即(2x+y)-(x+y)=16-10
新课学习
用①-②也能消去未知数y,得(x+y)-(2x+y)=10-16
解:①-②得x-2x=10-16
-x=-6
x=6
把x=6代入①得y=4
所以这个方程组的解是
解二元一次方程组
新课学习
用加减法解方程组:
例1
导引:
两个方程中x的系数相同,y的系数互为相反数,
这样可以把两个方程相加消去y,或者把两个方
程相减消去x.
解:
此题中未知数的系数有什么新的关系?你能想到什么办法消元?
新课学习
方法一:①+②,得6x=12,解得x=2.把x=2
代入②,得3×2+7y=13,解得y=1.
所以原方程组的解为
方法二:①-②,得-14y=-14,解得y=1.
把y=1代入①,得3x-7×1=-1,解得x=2.
所以原方程组的解为
新课学习
加减法定义:当二元一次方程组的两个方程中同
一未知数的系数相反或相等时,把这两个方程的两边
分别相加或相减,就能消去这个未知数,得到一个一
元一次方程,这种方法叫做加减消元法,简称加减法.
新课学习
二元一次方程组
系数相同,相减消元
消元
加减
一元一次方程
转化
同一未知数
系数相反,相加消元
前提
新课学习
用加减法解方程组:
例2
在方程两边乘适当的数,变形成同一未知数在两个方程中的系数相反或相等.
直接加减是否可行?
不可行
怎样实现方程组中存在系数相同或相反的未知数,进而使用加减消元法呢?
新课学习
解:
①×3,得 9x+12y=48. ③
②×2,得 10x-12y=66. ④
③+④,得19x=114,
即 x=6.
把x=6代入① ,得 3×6+4y=16,
4y= -2,
y=
所以这个方程组的解是
新课学习
思考:对于一些系数不同或不互为相反数的二元一次方程组,还能用加减法来解吗
先变形,再加减消元
化归思想:将复杂问题通过变换转化为简单问题;将难解的问题通过变换转化为容易求解的问题;将未解决的问题通过变换转化为已解决的问题.这就是解决数学问题常用的化归思想.
新课学习
例3 解方程组:
导引:方程组中,两个方程中y的系数的绝对值成倍数
关系,方程②乘以3就可与方程①相加消去y.
解: 由②×3,得 51x-9y=222,③
由①+③,得 59x=295,解得 x=5.
把x=5代入①,得8×5+9y=73,解得
所以原方程组的解为
新课学习
1
2
3
思想:
消元
转化
解决
前提:
二元一次方程组的两个方程中同一未知数的系数相反或相等
步骤:
变形
加减
求解
回代
写解
二元
一元
用加减法消元法解二元一次方程组:
新课学习
课后练习
1、 用加减法解方程组:
①+②,得4x=8,
解这个方程,得x=2.
把x=2代入①,得y= .
因此,这个方程组的解是
解:
①×2,得10x+4y=50.③
③-②,得7x=35,解这个方程,得x=5.
把x=5代入①,得5×5+2y=25,y=0.
因此,这个方程组的解是
解:
用加减法解方程组 时,要使两个方程中同一未知数的系数相等或相反,有以下四种变形的结果:
其中变形正确的是( )
A.①② B.③④ C.①③ D.②④
B
2、
THANKS
