18.1.2.2 平行四边形的判定(第2课时)(同步课件)-八年级数学下册同步精品课堂(人教版)
文档属性
| 名称 | 18.1.2.2 平行四边形的判定(第2课时)(同步课件)-八年级数学下册同步精品课堂(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 34.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-25 11:24:10 | ||
图片预览







文档简介
(共24张PPT)
第18章
平行四边形
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
18.1.2.2
平行四边形的
判定(2)
情景引入
高铁被外媒誉为我国新四大发明之一,我们知道铁路的两条直铺的铁轨互相平行,那么铁路工人是怎样的确保它们平行的呢?
情景引入
B
A
如图,将线段AB向右平移BC长度后得到线段CD,连接AD,BC,由此你能猜想四边形ABCD的形状吗?
D
C
四边形ABCD是平行四边形
一组对边平行且相等的四边形是平行四边形.
思考:
猜想:
新知探究
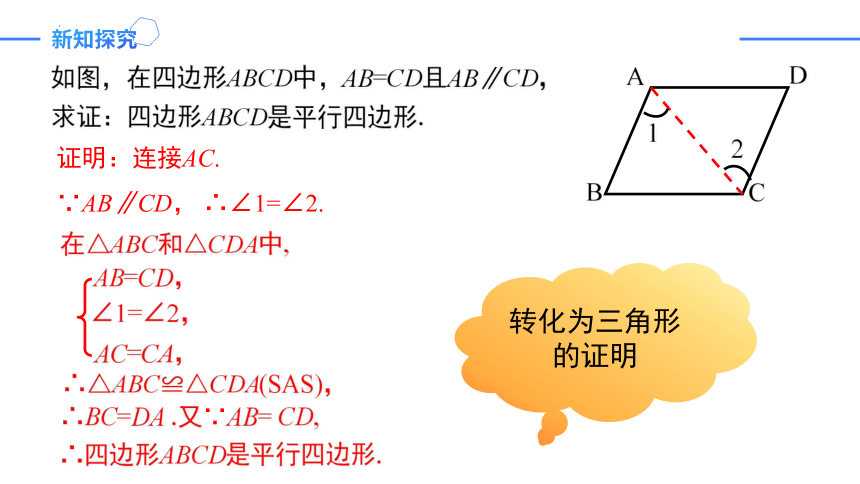
如图,在四边形ABCD中,AB=CD且AB∥CD,
求证:四边形ABCD是平行四边形.
A
B
C
D
2
1
证明:连接AC.
∵AB∥CD, ∴∠1=∠2.
在△ABC和△CDA中,
AB=CD,
AC=CA,
∠1=∠2,
∴△ABC≌△CDA(SAS),
∴BC=DA .又∵AB= CD,
∴四边形ABCD是平行四边形.
转化为三角形的证明
平行四边形的判定5
新知探究
一组对边平行且相等的四边形是平行四边形.
几何语言:
在四边形ABCD中,∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形.
B
D
A
C
典例精析
例1
A
B
C
D
E
F
证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD∥ EF,AD=EF,
EF∥ BC, EF=BC.
∴AD∥ BC,AD=BC.
∴四边形ABCD是平行四边形.
四边形AEFD和EBCF都是平行四边形,求证:四边形ABCD 是平行四边形.
典例精析
例2
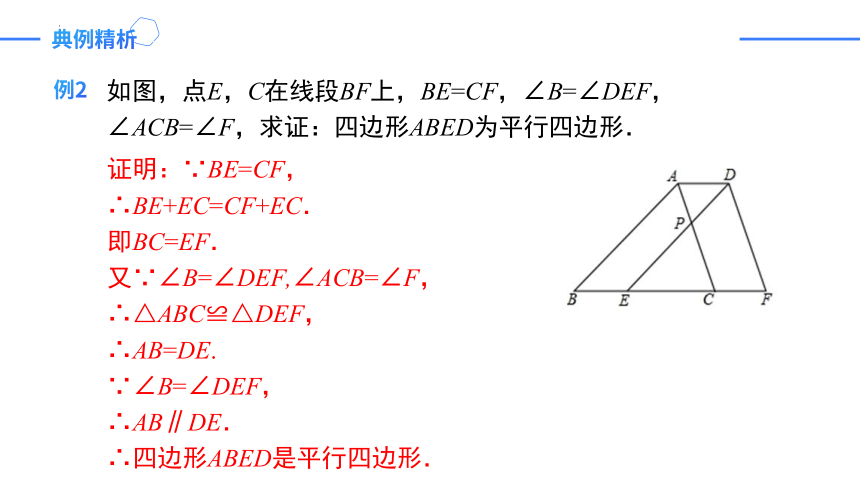
如图,点E,C在线段BF上,BE=CF,∠B=∠DEF,∠ACB=∠F,求证:四边形ABED为平行四边形.
证明:∵BE=CF,
∴BE+EC=CF+EC.
即BC=EF.
又∵∠B=∠DEF,∠ACB=∠F,
∴△ABC≌△DEF,
∴AB=DE.
∵∠B=∠DEF,
∴AB∥DE.
∴四边形ABED是平行四边形.
典例精析
例3
在四边形 ABCD 中 , 已知 AD ∥ BC, 若再添加一个条件 , 能使四边形 ABCD 成为平行四边形 , 则这个条件可以 是_________________
( 写出一个条件即可 , 不再添加辅助线 ) .
分析 平行添加条件 AD = BC, 可得出该四边形是平行四边形 .
∵ AD ∥ BC, AD = BC, ∴ 四边形 ABCD 是平行四边形 ( 一组对边平行且相等的四边形是平行四边形 ) .
AD = BC ( 答案不唯一 )
典例精析
例4
已知:如图 , 在四边形 ABCD 中 , AD ∥ BC,E 是 CD 的中点 . BE 的延长线与 AD 的延长线相交于点 F, 连接 BD, CF. 判断四边形 BCFD 的形状 , 并证明你的结论 .
典例精析
例4
解 四边形 BCFD 是平行四边形 .
证明:因为 E 是 CD 的中点 , 所以 DE = CE.
又因为 AD ∥ BC, 点 F 在 AD 的延长线上 ,
所以 ∠ DFE =∠ CBE, ∠ FDE =∠ BCE.
在 △ FDE 与 △ BCE 中 ,
∵ ∠ DFE =∠ CBE, ∠ FDE =∠ BCE, DE = CE,
所以 △ FDE ≌ △ BCE ( AAS ) , 所以 DF = BC.
又因为 DF ∥ BC, 所以四边形 BCFD 是平行四边形 .
典例精析
例5
如图 , 点 B, E, C, F 在一条直线上 , AB =DF, AC = DE, BE = FC.
(1) 求证: △ ABC ≌ △ DFE ;
(2) 连接 AF, BD, 求证:四边形 ABDF 是平行四边形.
典例精析
例5
解 (1) 证明: ∵ BE = FC, ∴ BC = FE.
在 △ ABC 和 △ DFE 中 ,
∵ AB = DF, AC = DE, BC = FE,
∴△ ABC ≌ △ DFE (SSS) .
(2) 由 (1) 知 △ ABC ≌ △ DFE,
∴∠ ABC =∠ DFE, ∴ AB ∥ DF.
又 ∵ AB = DF, ∴ 四边形 ABDF 是平行四边形 .
选择判定定理的技巧
归纳总结
典例精析
例6
如 图 , 四边形 ABCD 的对角线AC ⊥ BD 于点 E, AB = BC, F为
四边形 ABCD 外的一点 , 且 ∠ FCA = 90 ° , ∠ CBF =∠ DCB .
(1)求证:四边形 DBFC 是平行四边形;
(2)如果 BC 平分 ∠ DBF, ∠ F = 45 ° , BD = 2 , 求 AC的长 .
解 (1) 证明: ∵ AC ⊥ BD, ∠ FCA = 90 ° ,
∴ BD ∥ CF.
∵∠ CBF =∠ DCB, ∴ CD ∥ BF,
∴ 四边形 DBFC 是平行四边形 .
典例精析
例6
(2) ∵ 四边形 DBFC 是平行四边形 , ∴ CF = BD = 2 .
∵ AB = BC, AC ⊥ BD, ∴ AE = CE.
如图 , 过点 C 作 CM ⊥ BF 于点 M.
∵ BC 平分 ∠ DBF, ∴ CE = CM.
∵∠ F = 45 ° ,
∴△ CFM 是等腰直角三角形 ,
从而 CM2 + MF2= 2 CM2=CF2, ∴ CM = CF = ,
∴ AE = CE = , ∴ AC = 2 .
典例精析
例7
如 图 , 已知 ABCD 的周长是 36 cm , 从钝角顶点 D 分别向AB, BC
引两条高 DE, DF, 且DE = 4 3 cm , DF = 5 3 cm , 求这个平行四边形的面积 .
解 设 AB = x cm ,BC = y cm .
∵ 四边形 ABCD 为平行四边形 , ∴ AB = CD, AD = BC.
又 ∵ 四边形 ABCD 的周长为 36 cm , ∴ 2 x + 2 y = 36 .
∵ DE ⊥ AB, DF ⊥ BC, ∴ S ABCD = AB · DE = BC · DF,
∴
∴ 解得
∴ S ABCD = AB · DE =10× = 40 ( cm2) .
2x +2y=36 ,
典例精析
例8
如 图 , 在四边形 ABCD 中 , AD ∥ BC, 且 AD > BC, BC = 6 cm ,
点 P, Q 分别从点 A, C同时出发 , 点 P 以 1 cm/s 的速度由点 A 向
点 D 运动 , 点 Q 以 2 cm/s 的速度由点 C 向点 B运动 . 当其中一点
到达终点时 , 另一点随之停止运动 . 几秒后四边形 BQP 是平行四边形?
解 ∵ AD ∥ BC, ∴ AP ∥ BQ.
只有当 AP = BQ 时 , 四边形 ABQP 是平行四边形 .
设 t 秒后四边形 ABQP 是平行四边形 ,
此时 , AP = t, BQ = 6 - 2 t,
∴ t = 6 - 2 t, 解得 t = 2 .
即 2 s 后四边形 ABQP 是平行四边形 .
归纳总结
平行四边形的判定(2)
平行四边形的性质与判定的综合运用
一组对边平行且相等的四边形是平行四边形.
当堂检测
1.已知四边形ABCD中有四个条件:AB∥CD,AB=CD,BC∥AD,BC=AD,从中任选两个,不能使四边形ABCD成为平行四边形的选法是 ( )
A.AB∥CD,AB=CD
B.AB∥CD,BC∥AD
C.AB∥CD,BC=AD
D.AB=CD,BC=AD
C
当堂检测
2.四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD.从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
B
O
D
A
C
B
当堂检测
3.在 ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是 ( )
A.AF=CE B.AE=CF
C.∠BAE=∠FCD D.∠BEA=∠FCE
B
4. 已知四边形ABCD中,AB∥CD,AB=CD,周长为20cm,两邻边的比是3:2,则较大边的长度是( )
A.4cm B.5cm
C.6cm D.7cm
C
当堂检测
5.如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC.求证:四边形BFCE是平行四边形.
证明:∵AB=CD,
∴AB+BC=CD+BC,即AC=BD,
在△ACE和△DBF中,
AC=BD ,∠A=∠D, AE=DF ,
∴△ACE≌△DBF(SAS),
∴CE=BF,∠ACE=∠DBF,
∴CE∥BF,
∴四边形BFCE是平行四边形.
当堂检测
证明:
∵四边形ABCD是平行四边形,
∴AB =CD,EB //FD.
又∵EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形.
6.如图 ,在平行四边形ABCD中,E,F分别是AB,CD的中点.求证:四边形EBFD是平行四边形.
第18章
平行四边形
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
18.1.2.2
平行四边形的
判定(2)
情景引入
高铁被外媒誉为我国新四大发明之一,我们知道铁路的两条直铺的铁轨互相平行,那么铁路工人是怎样的确保它们平行的呢?
情景引入
B
A
如图,将线段AB向右平移BC长度后得到线段CD,连接AD,BC,由此你能猜想四边形ABCD的形状吗?
D
C
四边形ABCD是平行四边形
一组对边平行且相等的四边形是平行四边形.
思考:
猜想:
新知探究
如图,在四边形ABCD中,AB=CD且AB∥CD,
求证:四边形ABCD是平行四边形.
A
B
C
D
2
1
证明:连接AC.
∵AB∥CD, ∴∠1=∠2.
在△ABC和△CDA中,
AB=CD,
AC=CA,
∠1=∠2,
∴△ABC≌△CDA(SAS),
∴BC=DA .又∵AB= CD,
∴四边形ABCD是平行四边形.
转化为三角形的证明
平行四边形的判定5
新知探究
一组对边平行且相等的四边形是平行四边形.
几何语言:
在四边形ABCD中,∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形.
B
D
A
C
典例精析
例1
A
B
C
D
E
F
证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD∥ EF,AD=EF,
EF∥ BC, EF=BC.
∴AD∥ BC,AD=BC.
∴四边形ABCD是平行四边形.
四边形AEFD和EBCF都是平行四边形,求证:四边形ABCD 是平行四边形.
典例精析
例2
如图,点E,C在线段BF上,BE=CF,∠B=∠DEF,∠ACB=∠F,求证:四边形ABED为平行四边形.
证明:∵BE=CF,
∴BE+EC=CF+EC.
即BC=EF.
又∵∠B=∠DEF,∠ACB=∠F,
∴△ABC≌△DEF,
∴AB=DE.
∵∠B=∠DEF,
∴AB∥DE.
∴四边形ABED是平行四边形.
典例精析
例3
在四边形 ABCD 中 , 已知 AD ∥ BC, 若再添加一个条件 , 能使四边形 ABCD 成为平行四边形 , 则这个条件可以 是_________________
( 写出一个条件即可 , 不再添加辅助线 ) .
分析 平行添加条件 AD = BC, 可得出该四边形是平行四边形 .
∵ AD ∥ BC, AD = BC, ∴ 四边形 ABCD 是平行四边形 ( 一组对边平行且相等的四边形是平行四边形 ) .
AD = BC ( 答案不唯一 )
典例精析
例4
已知:如图 , 在四边形 ABCD 中 , AD ∥ BC,E 是 CD 的中点 . BE 的延长线与 AD 的延长线相交于点 F, 连接 BD, CF. 判断四边形 BCFD 的形状 , 并证明你的结论 .
典例精析
例4
解 四边形 BCFD 是平行四边形 .
证明:因为 E 是 CD 的中点 , 所以 DE = CE.
又因为 AD ∥ BC, 点 F 在 AD 的延长线上 ,
所以 ∠ DFE =∠ CBE, ∠ FDE =∠ BCE.
在 △ FDE 与 △ BCE 中 ,
∵ ∠ DFE =∠ CBE, ∠ FDE =∠ BCE, DE = CE,
所以 △ FDE ≌ △ BCE ( AAS ) , 所以 DF = BC.
又因为 DF ∥ BC, 所以四边形 BCFD 是平行四边形 .
典例精析
例5
如图 , 点 B, E, C, F 在一条直线上 , AB =DF, AC = DE, BE = FC.
(1) 求证: △ ABC ≌ △ DFE ;
(2) 连接 AF, BD, 求证:四边形 ABDF 是平行四边形.
典例精析
例5
解 (1) 证明: ∵ BE = FC, ∴ BC = FE.
在 △ ABC 和 △ DFE 中 ,
∵ AB = DF, AC = DE, BC = FE,
∴△ ABC ≌ △ DFE (SSS) .
(2) 由 (1) 知 △ ABC ≌ △ DFE,
∴∠ ABC =∠ DFE, ∴ AB ∥ DF.
又 ∵ AB = DF, ∴ 四边形 ABDF 是平行四边形 .
选择判定定理的技巧
归纳总结
典例精析
例6
如 图 , 四边形 ABCD 的对角线AC ⊥ BD 于点 E, AB = BC, F为
四边形 ABCD 外的一点 , 且 ∠ FCA = 90 ° , ∠ CBF =∠ DCB .
(1)求证:四边形 DBFC 是平行四边形;
(2)如果 BC 平分 ∠ DBF, ∠ F = 45 ° , BD = 2 , 求 AC的长 .
解 (1) 证明: ∵ AC ⊥ BD, ∠ FCA = 90 ° ,
∴ BD ∥ CF.
∵∠ CBF =∠ DCB, ∴ CD ∥ BF,
∴ 四边形 DBFC 是平行四边形 .
典例精析
例6
(2) ∵ 四边形 DBFC 是平行四边形 , ∴ CF = BD = 2 .
∵ AB = BC, AC ⊥ BD, ∴ AE = CE.
如图 , 过点 C 作 CM ⊥ BF 于点 M.
∵ BC 平分 ∠ DBF, ∴ CE = CM.
∵∠ F = 45 ° ,
∴△ CFM 是等腰直角三角形 ,
从而 CM2 + MF2= 2 CM2=CF2, ∴ CM = CF = ,
∴ AE = CE = , ∴ AC = 2 .
典例精析
例7
如 图 , 已知 ABCD 的周长是 36 cm , 从钝角顶点 D 分别向AB, BC
引两条高 DE, DF, 且DE = 4 3 cm , DF = 5 3 cm , 求这个平行四边形的面积 .
解 设 AB = x cm ,BC = y cm .
∵ 四边形 ABCD 为平行四边形 , ∴ AB = CD, AD = BC.
又 ∵ 四边形 ABCD 的周长为 36 cm , ∴ 2 x + 2 y = 36 .
∵ DE ⊥ AB, DF ⊥ BC, ∴ S ABCD = AB · DE = BC · DF,
∴
∴ 解得
∴ S ABCD = AB · DE =10× = 40 ( cm2) .
2x +2y=36 ,
典例精析
例8
如 图 , 在四边形 ABCD 中 , AD ∥ BC, 且 AD > BC, BC = 6 cm ,
点 P, Q 分别从点 A, C同时出发 , 点 P 以 1 cm/s 的速度由点 A 向
点 D 运动 , 点 Q 以 2 cm/s 的速度由点 C 向点 B运动 . 当其中一点
到达终点时 , 另一点随之停止运动 . 几秒后四边形 BQP 是平行四边形?
解 ∵ AD ∥ BC, ∴ AP ∥ BQ.
只有当 AP = BQ 时 , 四边形 ABQP 是平行四边形 .
设 t 秒后四边形 ABQP 是平行四边形 ,
此时 , AP = t, BQ = 6 - 2 t,
∴ t = 6 - 2 t, 解得 t = 2 .
即 2 s 后四边形 ABQP 是平行四边形 .
归纳总结
平行四边形的判定(2)
平行四边形的性质与判定的综合运用
一组对边平行且相等的四边形是平行四边形.
当堂检测
1.已知四边形ABCD中有四个条件:AB∥CD,AB=CD,BC∥AD,BC=AD,从中任选两个,不能使四边形ABCD成为平行四边形的选法是 ( )
A.AB∥CD,AB=CD
B.AB∥CD,BC∥AD
C.AB∥CD,BC=AD
D.AB=CD,BC=AD
C
当堂检测
2.四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD.从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
B
O
D
A
C
B
当堂检测
3.在 ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是 ( )
A.AF=CE B.AE=CF
C.∠BAE=∠FCD D.∠BEA=∠FCE
B
4. 已知四边形ABCD中,AB∥CD,AB=CD,周长为20cm,两邻边的比是3:2,则较大边的长度是( )
A.4cm B.5cm
C.6cm D.7cm
C
当堂检测
5.如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC.求证:四边形BFCE是平行四边形.
证明:∵AB=CD,
∴AB+BC=CD+BC,即AC=BD,
在△ACE和△DBF中,
AC=BD ,∠A=∠D, AE=DF ,
∴△ACE≌△DBF(SAS),
∴CE=BF,∠ACE=∠DBF,
∴CE∥BF,
∴四边形BFCE是平行四边形.
当堂检测
证明:
∵四边形ABCD是平行四边形,
∴AB =CD,EB //FD.
又∵EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形.
6.如图 ,在平行四边形ABCD中,E,F分别是AB,CD的中点.求证:四边形EBFD是平行四边形.
