第9章 整式乘法与因式分解 章末复习 课件(共28张PPT)-七年级数学下册同步精品课堂(苏科版)
文档属性
| 名称 | 第9章 整式乘法与因式分解 章末复习 课件(共28张PPT)-七年级数学下册同步精品课堂(苏科版) |  | |
| 格式 | pptx | ||
| 文件大小 | 34.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-25 12:21:45 | ||
图片预览








文档简介
(共28张PPT)
第9章 整式乘法与因式分解
章末复习
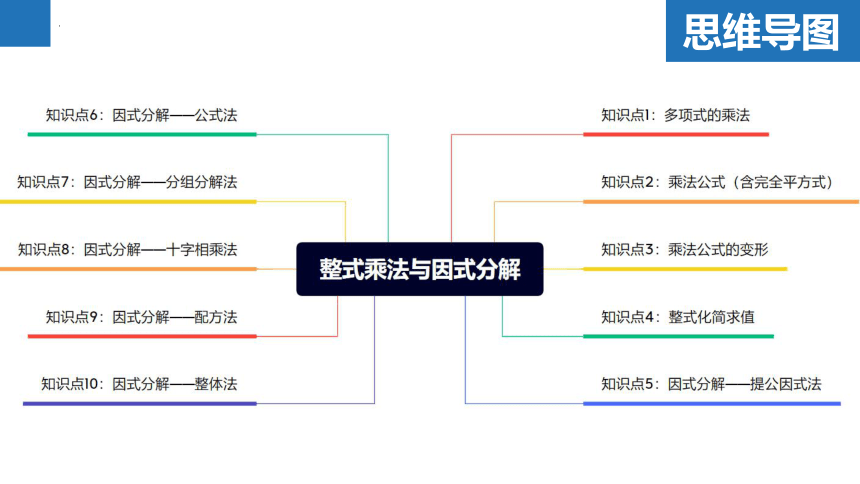
思维导图
知识点1:多项式的乘法
多项式与多项式相乘 运算性质
注意点
先用一个多项式的每一项乘另一个多项式的每一项
再把所得的积相加
能合并同类项的最后要合并同类项
相乘时,按一定的顺序进行,必须做到不重不漏
相乘所得的积的项数,在合并同类项之前,应等于原多项式的项数之积
最后的结果要合并同类项
例1、若(x2+ax+2)(2x-4)的结果中不含x2项,则a的值为( )
A.0 B.2 C. D.-2
【分析】(x2+ax+2)(2x-4)
=2x3+2ax2+4x-4x2-4ax-8
=2x3+(2a-4)x2+(4-4a)x-8,
典例精析
B
∵(x2+ax+2)(2x-4)的结果中不含x2项,
∴2a-4=0,解得:a=2。
知识点2:乘法公式(含完全平方式)
乘法公式(含完全平方式) 完全平方公式 口诀
平方差公式
完全平方式 (a±b)2=a2±2ab+b2
(a+b)(a-b)=a2-b2
首平方,尾平方,积的两倍在中央(符号随中央)
一同一反,平方相减
若A2±2AB+B2=(A±B)2,则A2±2AB+B2为完全平方式
例2-1、计算:(a-2b)(-2b-a)-(a-2b)2。
【分析】原式=4b2-a2-(a2-4ab+4b2)
=-2a2+4ab。
典例精析
例2-2、已知9y2-my+4是完全平方式,则m的值为( )
A.6 B.±6 C.12 D.±12
【分析】(3y±2)2=9y2±12y+4=9y2-my+4,解得:m=±12。
典例精析
D
知识点3:乘法公式的变形
(a±b)2=a2±2ab+b2的变形(知二求一) 已知a±b、a2+b2,求ab
已知a±b、ab,求a2+b2
已知a2+b2、ab,求a±b
ab=,ab=
a2+b2=(a+b)2-2ab,a2+b2=(a-b)2+2ab
a+b=±,a-b=±
知识点3:乘法公式的变形
(a+b)2-(a-b)2=4ab的变形(知二求一) 已知a+b、a-b,求ab
已知a+b、ab,求a-b
已知a-b、ab,求a+b
ab=
a-b=±
a+b=±
知识点3:乘法公式的变形
(a+b)2+(a-b)2=2(a2+b2)的变形(知二求一) 已知a+b、a-b,求a2+b2
已知a+b、a2+b2,求a-b
已知a-b、a2+b2,求a+b
a2+b2=
a-b=±
a+b=±
例3-1、已知a-b=1,a2+b2=25,则ab的值为( )
A.6 B.12 C.13 D.24
【分析】
(a-b)2=a2+b2-2ab=25-2ab=12=1,解得:ab=12。
典例精析
B
例3-2、若a+b=5,ab=1,则(a-b)2的值( )
A.1 B.9 C.16 D.21
【分析】
(a-b)2=(a+b)2-4ab=52-4×1=21。
典例精析
D
例3-3、已知(x+y)2=49,x2+y2=30,则(x-y)2的值为________。
【分析】
(x-y)2=2(x2+y2)-(x+y)2=2×30-49=11。
典例精析
11
知识点4:整式化简求值
步骤 所用知识点
整式化简
先化简
后求值
多项式的乘法
乘法公式
例4、先化简,再求值:[2(x-y)]2-(16x2y4-12x3y3)÷(2xy)2,其中x=-,y=-3。
【分析】[2(x-y)]2-(16x2y4-12x3y3)÷(2xy)2
=4(x-y)2-(16x2y4-12x3y3)÷4x2y2
=4x2-8xy+4y2-(4y2-3xy)
=4x2-5xy,
典例精析
当x=-,y=-3时,原式=4×(-)2-5×(-)×(-3)=1-=-。
知识点5:因式分解——提公因式法
提公因式法 概念
注意点
AB+AC+AD=A(B+C+D)(A为公因式)
因式分解的第一步应为提公因式
若多项式第一项是负的,一般要提出“-”号,使括号内的第一项的系数成为正数;提出“-”号时,多项式的各项要变号
A有可能是单项式,也有可能是多项式,要有整体思想
提A要彻底!
例5、分解因式:-8a3b2-12a3bc+4a2b。
【分析】原式=-4a2b(2ab+3ac-1)。
典例精析
知识点6:因式分解——公式法
公式法 概念
注意点
a2±2ab+b2=(a±b)2
a2-b2=(a+b)(a-b)
若为三项式,优先考虑逆用完全平方公式;
若为二项式,优先考虑逆用平方差公式
a、b有可能是单项式,也有可能是多项式,要有整体思想
例6-1、分解因式:
(1)2x4-4x2y2+2y4;
(2)(y+2x)2-(x+2y)2。
【分析】
(1)原式=2(x4-2x2y2+y4)=2(x2-y2)2=[(x+y)(x-y)]2=(x+y)2(x-y)2;
典例精析
(2)原式=(y+2x+x+2y)(y+2x-x-2y)=(3x+3y)(x-y)=3(x+y)(x-y)。
例6-2、若2112-422×111+1112=k+992-1,则k的值是( )
A.100 B.198 C.200 D.205
【分析】由题意可得:
2112-2×211×111+1112=k+992-1,(211-111)2=k+992-1,1002=k+992-1,
∴k=1002-992+1=(100+99)×(100-99)+1=199+1=200。
典例精析
C
知识点7:因式分解——分组分解法
分组分解法 常见的分组类型
举例 ax+bx+ay+by a2-b2+ac-bc a2±2ab+b2+c
注意点 一般地,因式分解一个四项式时,若其中三项可以构成完全平方式,则为三一分组,否则为二二分组
二二分组 三一分组
ax+bx+ay+by a2-b2+ac-bc
=x(a+b)+y(a+b) =(a+b)(x+y) =(a+b)(a-b)+c(a-=(a-b)(a+b+c)
a2±2ab+b2+c
=(a±b)2+c
例7、分解因式:
(1)x3+2x2y-4x-8y;
(2)m2-2m+1-4n2。
典例精析
【分析】
(1)原式=x2(x+2y)-4(x+2y)=(x+2y)(x2-4)=(x+2y)(x+2)(x-2);
(2)原式=(m-1)2-4n2=(m+2n-1)(m-2n-1)。
知识点8:因式分解——十字相乘法
十字相乘法 二次项系数为1
二次项系数不为1 注意点 x2+(p+q)x+pq=(x+p)(x+q) x2+(p+q)xy+pqy2=(x+py)(x+qy)
ax2+bx+c=(a1x+c1)(a2x+c2)
(a≠0,a=a1a2,c=c1c2,b=a1c2+a2c1)
十字相乘法主要适用于二次三项式
例8、分解因式:
(1)x4+5x2-36;
(2)(x2+2x)2-2(x2+2x)-3。
典例精析
【分析】
(1)原式=(x2+9)(x2-4)=(x2+9)(x+2)(x-2);
(2)原式=(x2+2x+1)(x2+2x-3)=(x+1)2(x+3)(x+1)。
知识点9:因式分解——配方法
配方法 举例 x2+2x-8
=x2+2x+1-9
=(x+1)2-9
=(x+1+3)(x+1-3)
=(x+4)(x-2)
例9、分解因式(配方法):4a2+4a-15。
【分析】
原式=4a2+4a+1-1-15
=(2a+1)2-16
=(2a+1+4)(2a+1-4)
=(2a+5)(2a-3)。
典例精析
知识点10:因式分解——整体法
整体法 举例 (a2-2a-3)(a2-2a+5)+16
令t=a2-2a,
原式=(t-3)(t+5)+16=t2+2t+1=(t+1)2,
将t=a2-2a还原,
原式=(a2-2a+1)2=(a-1)4
例10、分解因式:(x2+x+1)(x2+x+2)-12。
【分析】令t=x2+x,
原式=(t+1)(t+2)-12=t2+3t-10=(t+5)(t-2),
将t=x2+x还原,
原式=(x2+x+5)(x2+x-2)=(x2+x+5)(x+2)(x-1)。
典例精析
第9章 整式乘法与因式分解
章末复习
思维导图
知识点1:多项式的乘法
多项式与多项式相乘 运算性质
注意点
先用一个多项式的每一项乘另一个多项式的每一项
再把所得的积相加
能合并同类项的最后要合并同类项
相乘时,按一定的顺序进行,必须做到不重不漏
相乘所得的积的项数,在合并同类项之前,应等于原多项式的项数之积
最后的结果要合并同类项
例1、若(x2+ax+2)(2x-4)的结果中不含x2项,则a的值为( )
A.0 B.2 C. D.-2
【分析】(x2+ax+2)(2x-4)
=2x3+2ax2+4x-4x2-4ax-8
=2x3+(2a-4)x2+(4-4a)x-8,
典例精析
B
∵(x2+ax+2)(2x-4)的结果中不含x2项,
∴2a-4=0,解得:a=2。
知识点2:乘法公式(含完全平方式)
乘法公式(含完全平方式) 完全平方公式 口诀
平方差公式
完全平方式 (a±b)2=a2±2ab+b2
(a+b)(a-b)=a2-b2
首平方,尾平方,积的两倍在中央(符号随中央)
一同一反,平方相减
若A2±2AB+B2=(A±B)2,则A2±2AB+B2为完全平方式
例2-1、计算:(a-2b)(-2b-a)-(a-2b)2。
【分析】原式=4b2-a2-(a2-4ab+4b2)
=-2a2+4ab。
典例精析
例2-2、已知9y2-my+4是完全平方式,则m的值为( )
A.6 B.±6 C.12 D.±12
【分析】(3y±2)2=9y2±12y+4=9y2-my+4,解得:m=±12。
典例精析
D
知识点3:乘法公式的变形
(a±b)2=a2±2ab+b2的变形(知二求一) 已知a±b、a2+b2,求ab
已知a±b、ab,求a2+b2
已知a2+b2、ab,求a±b
ab=,ab=
a2+b2=(a+b)2-2ab,a2+b2=(a-b)2+2ab
a+b=±,a-b=±
知识点3:乘法公式的变形
(a+b)2-(a-b)2=4ab的变形(知二求一) 已知a+b、a-b,求ab
已知a+b、ab,求a-b
已知a-b、ab,求a+b
ab=
a-b=±
a+b=±
知识点3:乘法公式的变形
(a+b)2+(a-b)2=2(a2+b2)的变形(知二求一) 已知a+b、a-b,求a2+b2
已知a+b、a2+b2,求a-b
已知a-b、a2+b2,求a+b
a2+b2=
a-b=±
a+b=±
例3-1、已知a-b=1,a2+b2=25,则ab的值为( )
A.6 B.12 C.13 D.24
【分析】
(a-b)2=a2+b2-2ab=25-2ab=12=1,解得:ab=12。
典例精析
B
例3-2、若a+b=5,ab=1,则(a-b)2的值( )
A.1 B.9 C.16 D.21
【分析】
(a-b)2=(a+b)2-4ab=52-4×1=21。
典例精析
D
例3-3、已知(x+y)2=49,x2+y2=30,则(x-y)2的值为________。
【分析】
(x-y)2=2(x2+y2)-(x+y)2=2×30-49=11。
典例精析
11
知识点4:整式化简求值
步骤 所用知识点
整式化简
先化简
后求值
多项式的乘法
乘法公式
例4、先化简,再求值:[2(x-y)]2-(16x2y4-12x3y3)÷(2xy)2,其中x=-,y=-3。
【分析】[2(x-y)]2-(16x2y4-12x3y3)÷(2xy)2
=4(x-y)2-(16x2y4-12x3y3)÷4x2y2
=4x2-8xy+4y2-(4y2-3xy)
=4x2-5xy,
典例精析
当x=-,y=-3时,原式=4×(-)2-5×(-)×(-3)=1-=-。
知识点5:因式分解——提公因式法
提公因式法 概念
注意点
AB+AC+AD=A(B+C+D)(A为公因式)
因式分解的第一步应为提公因式
若多项式第一项是负的,一般要提出“-”号,使括号内的第一项的系数成为正数;提出“-”号时,多项式的各项要变号
A有可能是单项式,也有可能是多项式,要有整体思想
提A要彻底!
例5、分解因式:-8a3b2-12a3bc+4a2b。
【分析】原式=-4a2b(2ab+3ac-1)。
典例精析
知识点6:因式分解——公式法
公式法 概念
注意点
a2±2ab+b2=(a±b)2
a2-b2=(a+b)(a-b)
若为三项式,优先考虑逆用完全平方公式;
若为二项式,优先考虑逆用平方差公式
a、b有可能是单项式,也有可能是多项式,要有整体思想
例6-1、分解因式:
(1)2x4-4x2y2+2y4;
(2)(y+2x)2-(x+2y)2。
【分析】
(1)原式=2(x4-2x2y2+y4)=2(x2-y2)2=[(x+y)(x-y)]2=(x+y)2(x-y)2;
典例精析
(2)原式=(y+2x+x+2y)(y+2x-x-2y)=(3x+3y)(x-y)=3(x+y)(x-y)。
例6-2、若2112-422×111+1112=k+992-1,则k的值是( )
A.100 B.198 C.200 D.205
【分析】由题意可得:
2112-2×211×111+1112=k+992-1,(211-111)2=k+992-1,1002=k+992-1,
∴k=1002-992+1=(100+99)×(100-99)+1=199+1=200。
典例精析
C
知识点7:因式分解——分组分解法
分组分解法 常见的分组类型
举例 ax+bx+ay+by a2-b2+ac-bc a2±2ab+b2+c
注意点 一般地,因式分解一个四项式时,若其中三项可以构成完全平方式,则为三一分组,否则为二二分组
二二分组 三一分组
ax+bx+ay+by a2-b2+ac-bc
=x(a+b)+y(a+b) =(a+b)(x+y) =(a+b)(a-b)+c(a-=(a-b)(a+b+c)
a2±2ab+b2+c
=(a±b)2+c
例7、分解因式:
(1)x3+2x2y-4x-8y;
(2)m2-2m+1-4n2。
典例精析
【分析】
(1)原式=x2(x+2y)-4(x+2y)=(x+2y)(x2-4)=(x+2y)(x+2)(x-2);
(2)原式=(m-1)2-4n2=(m+2n-1)(m-2n-1)。
知识点8:因式分解——十字相乘法
十字相乘法 二次项系数为1
二次项系数不为1 注意点 x2+(p+q)x+pq=(x+p)(x+q) x2+(p+q)xy+pqy2=(x+py)(x+qy)
ax2+bx+c=(a1x+c1)(a2x+c2)
(a≠0,a=a1a2,c=c1c2,b=a1c2+a2c1)
十字相乘法主要适用于二次三项式
例8、分解因式:
(1)x4+5x2-36;
(2)(x2+2x)2-2(x2+2x)-3。
典例精析
【分析】
(1)原式=(x2+9)(x2-4)=(x2+9)(x+2)(x-2);
(2)原式=(x2+2x+1)(x2+2x-3)=(x+1)2(x+3)(x+1)。
知识点9:因式分解——配方法
配方法 举例 x2+2x-8
=x2+2x+1-9
=(x+1)2-9
=(x+1+3)(x+1-3)
=(x+4)(x-2)
例9、分解因式(配方法):4a2+4a-15。
【分析】
原式=4a2+4a+1-1-15
=(2a+1)2-16
=(2a+1+4)(2a+1-4)
=(2a+5)(2a-3)。
典例精析
知识点10:因式分解——整体法
整体法 举例 (a2-2a-3)(a2-2a+5)+16
令t=a2-2a,
原式=(t-3)(t+5)+16=t2+2t+1=(t+1)2,
将t=a2-2a还原,
原式=(a2-2a+1)2=(a-1)4
例10、分解因式:(x2+x+1)(x2+x+2)-12。
【分析】令t=x2+x,
原式=(t+1)(t+2)-12=t2+3t-10=(t+5)(t-2),
将t=x2+x还原,
原式=(x2+x+5)(x2+x-2)=(x2+x+5)(x+2)(x-1)。
典例精析
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
