北师大版2024年七年级下册 第2章 相交线与平行线 单元测试卷(含解析)
文档属性
| 名称 | 北师大版2024年七年级下册 第2章 相交线与平行线 单元测试卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 419.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 00:00:00 | ||
图片预览



文档简介
北师大版2024年七年级下册 第2章 相交线与平行线 单元测试卷
满分100分
一.选择题(共10小题,满分30分,每小题3分)
1.下列图形中,线段AD的长度表示点A到直线BC距离的是( )
A.B.C.D.
2.平面内有五条直线两两相交,设最多交点个数为a,最少交点个数为b,则a+b的值是( )
A.9 B.10 C.11 D.14
3.如图,直线AB,CD相交于点O,若射线OP平分∠AOD,射线OD平分∠BOP,则∠BOC的度数为( )
A.115° B.120° C.125° D.130°
4.两条直线被第三条直线所截,形成了常说的“三线八角”.为了便于记忆,同学们可用双手表示“三线八角”(两大拇指代表被截直线,两只食指在同一直线上代表截线),如图,它们构成的一对角可以看成( )
A.同位角 B.同旁内角 C.内错角 D.对顶角
5.如图,下列条件中,能判定AB∥CD的是( )
A.∠1=∠4 B.∠1=∠3 C.∠5=∠ADC D.∠2=∠4
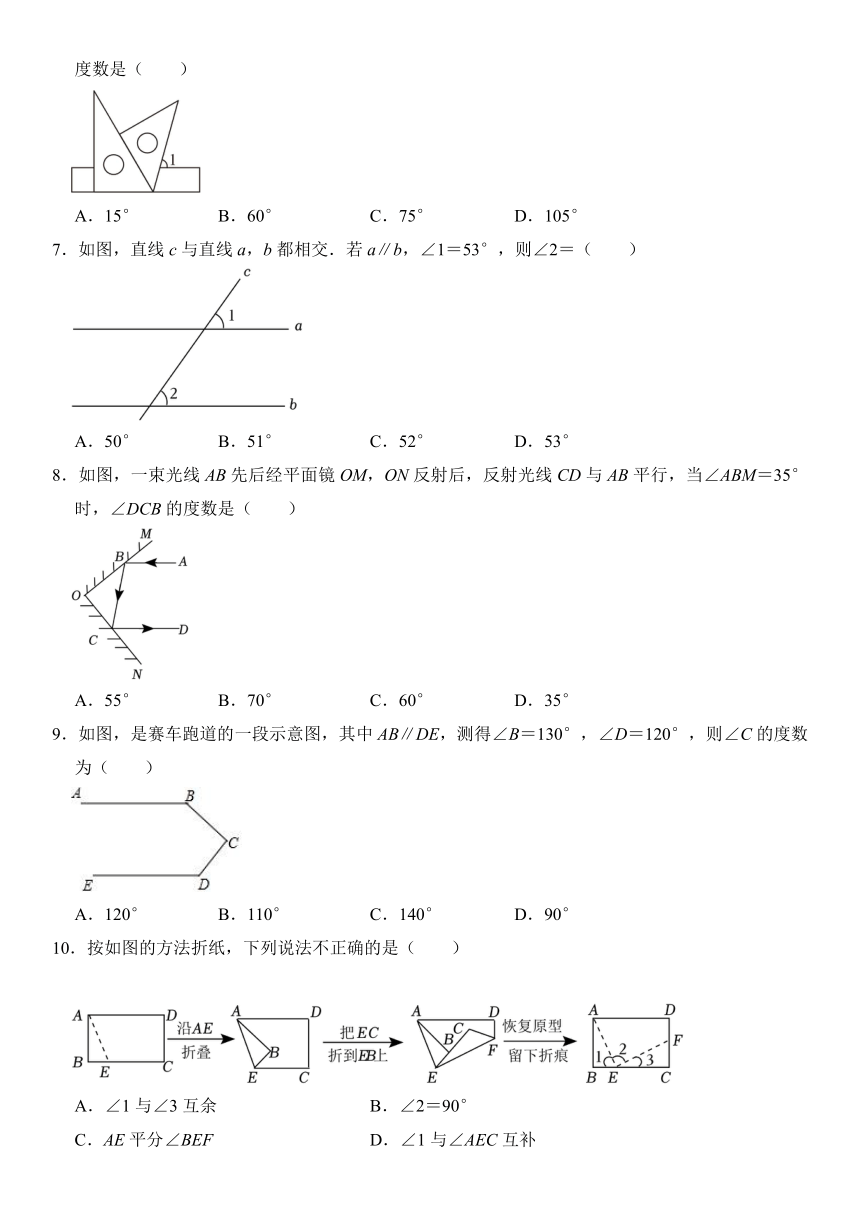
6.将一副三角板(含30°,45°,60°,90°角)按如图所示的位置摆放在直尺上,则∠1的余角度数是( )
A.15° B.60° C.75° D.105°
7.如图,直线c与直线a,b都相交.若a∥b,∠1=53°,则∠2=( )
A.50° B.51° C.52° D.53°
8.如图,一束光线AB先后经平面镜OM,ON反射后,反射光线CD与AB平行,当∠ABM=35°时,∠DCB的度数是( )
A.55° B.70° C.60° D.35°
9.如图,是赛车跑道的一段示意图,其中AB∥DE,测得∠B=130°,∠D=120°,则∠C的度数为( )
A.120° B.110° C.140° D.90°
10.按如图的方法折纸,下列说法不正确的是( )
A.∠1与∠3互余 B.∠2=90°
C.AE平分∠BEF D.∠1与∠AEC互补
二.填空题(共6小题,满分18分,每小题3分)
11.如图,直线AB,CD被AE所截,则∠A的同旁内角是 .
12.如图,直线l表示一段河道,点P表示村庄,现要从河l向村庄P引水,图中有四种方案,其中沿线段PC路线开挖的水渠长最短,理由是 .
13.如图是一种对顶角量角器,它所测量的角的度数是 ,用它测量角的原理是 .
14.已知∠1与∠2互余,且∠1=35°,则∠2的补角的度数为 度.
15.如图,直线l1∥l2,将直角三角板按如图方式放置,直角顶点在l2上,若∠1=40°,则∠2= .
16.如图,直线EF上有两点A、C,分别引两条射线AB、CD,∠DCF=60°,∠EAB=70°,射线AB、CD分别绕A点,C点以1度/秒和3度/秒的速度同时顺时针转动,在射线CD转动一周的时间内,使得CD与AB平行所有满足条件的时间= .
三.解答题(共7小题,满分52分)
17.(5分)如图,直线AB、CD相交于点O,OE平分∠BOD,∠BOE=36°.求∠AOC的度数.
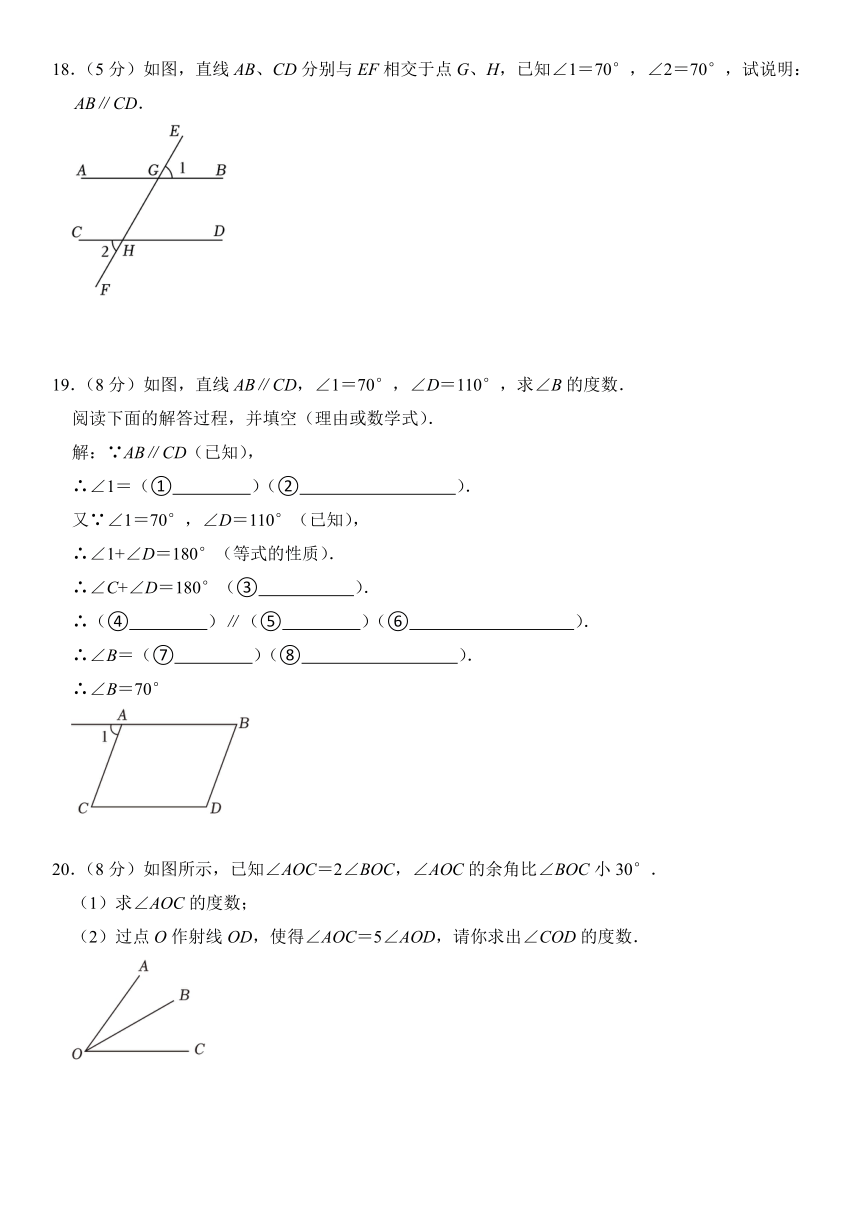
18.(5分)如图,直线AB、CD分别与EF相交于点G、H,已知∠1=70°,∠2=70°,试说明:AB∥CD.
19.(8分)如图,直线AB∥CD,∠1=70°,∠D=110°,求∠B的度数.
阅读下面的解答过程,并填空(理由或数学式).
解:∵AB∥CD(已知),
∴∠1=(① )(② ).
又∵∠1=70°,∠D=110°(已知),
∴∠1+∠D=180°(等式的性质).
∴∠C+∠D=180°(③ ).
∴(④ )∥(⑤ )(⑥ ).
∴∠B=(⑦ )(⑧ ).
∴∠B=70°
20.(8分)如图所示,已知∠AOC=2∠BOC,∠AOC的余角比∠BOC小30°.
(1)求∠AOC的度数;
(2)过点O作射线OD,使得∠AOC=5∠AOD,请你求出∠COD的度数.
21.(8分)如图,∠1=∠C,BE⊥DF于点P.
(1)若∠2=55°,请求出∠B的度数;
(2)若∠2+∠D=90°,求证:AB∥CD.
22.(9分)定义:如果有三个角α,β,γ,满足α+β﹣γ=90°,则称γ是α和β的“减余角”.
(1)已知∠1=37°,∠2=66°,若∠3是∠1和∠2的“减余角”,则∠3= .
(2)现有一张正方形纸片ABCD,如图1所示,点E为线段BC上一点(不与B、C重合).连结AE,将纸片沿着AE对折,使点B落在正方形纸片的内部且对应点为B′.
①若∠B′EC是∠AEB和∠AEB′的“减余角”,求∠AEB的度数.
②再将此正方形纸片沿着B′E所在直线对折,使点C落在正方形纸片的内部且对应点为C′,如图2所示.是否存在∠AEB,∠AEC′,∠B′EC中的一个角是其它两个角的“减余角”?若存在,请求出∠AEB的度数;若不存在,请说明理由.
23.(9分)综合与探究
问题情境
在综合实践课上,老师组织七年级(2)班的同学开展了探究两角之间数量关系的数学活动,如图,已知射线AM∥BN,连接AB,点P是射线AM上的一个动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
探索发现
“快乐小组”经过探索后发现:
(1)当∠A=60°时,∠CBD=∠A.请说明理由.
(2)不断改变∠A的度数,∠CBD与∠A却始终存在某种数量关系,用含∠A的式子表示∠CBD为 .
操作探究
(3)“智慧小组”利用量角器量出∠APB和∠ADB的度数后,探究二者之间的数量关系.他们惊奇地发现,当点P在射线AM上运动时,无论点P在AM上的什么位置,∠APB与∠ADB之间的数量关系都保持不变,请写出它们的关系,并说明理由.
(4)点P继续在射线AM上运动,当运动到使∠ACB=∠ABD时,请直接写出2∠ABC+∠A的结果.
参考答案
一.选择题
1.解:A.AD与BC不垂直,故线段AD的长不能表示点A到直线BC距离,不合题意.
B.AD与BC不垂直,故线段AD的长不能表示点A到直线BC距离,不合题意;
C.AD与BC不垂直,故线段AD的长不能表示点A到直线BC距离,不合题意;
D.AD⊥BC于D,则线段AD的长表示点A到直线BC的距离,符合题意;
故选:D.
2.解:平面内有五条直线两两相交,最多交点个数为a==10,最少交点个数为b=1,
∴a+b=10+1=11.
故选:C.
3.解:∵射线OP平分∠AOD,射线OD平分∠BOP,
∴∠AOP=∠POD=∠BOD,
∵∠AOP+∠POD+∠BOD=180°,
∴∠BOD=60°.
∴∠AOC=∠BOD=60°.
∵∠BOC+∠AOC=180°,
∴∠BOC=120°.
故选:B.
4.解:用双手表示“三线八角”(两大拇指代表被截直线,两只食指在同一直线上代表截线),如图,它们构成的一对角可以看成同位角.
故选:A.
5.解:A.∠1=∠4,不能判定AB∥CD,故该选项不正确,不符合题意;
B.∵∠1=∠3,∴AB∥CD,故该选项正确,符合题意;
C.∵∠5=∠ADC,∴AD∥BC,故该选项不正确,不符合题意;
D.∠2=∠4,∴AD∥BC,故该选项不正确,不符合题意;
故选:B.
6.解:如下图所示:
依题意得:∠2=45°,∠3=60°,
∴∠2+∠3=105°,
∵∠4+∠2+∠3=180°,
∴∠4=75°,
根据直尺的对边平行得∠1=∠4=75°,
∴∠1的余角为:90°﹣∠1=90°﹣75°=15°.
故选:A.
7.解:∵a∥b,
∴∠1=∠2,
∵∠1=53°,
∴∠2=53°.
故选:D.
8.解:由反射定律得到:∠OBC=∠ABM=35°,
∴∠ABC=180°﹣35°﹣35°=110°,
∵AB∥CD,
∴∠BCD+∠ABC=180°,
∴∠BCD=70°.
故选:B.
9.解:如图所示:过点C作CF∥AB.
∵AB∥DE,
∴DE∥CF;
∴∠BCF=180°﹣∠B=50°,∠DCF=180°﹣∠D=60°;
∴∠C=∠BCF+∠DCF=110°.
故选:B.
10.解:根据折叠的性质可知,∠1=∠AEB,∠3=∠FEC,
∵∠1+∠AEB+∠3+∠FEC=180°,
∴2(∠1+∠3)=180°,即∠1+∠3=90°,故A不符合题意;
∴∠2=90°,故B不符合题意,C符合题意;
∵∠1+∠AEC=180°,故D不符合题意.
故选:C.
二.填空题
11.解:∵直线AB,CD被AE所截,
∴∠A的同旁内角是∠AOC.
故答案为:∠AOC.
12.解:沿线段PC路线开挖的水渠长最短,理由是垂线段最短.
故答案为:垂线段最短.
13.解:由量角器的读数可知,所测量角的度数为30°,
原理:对顶角相等,
故答案为:30°,对顶角相等.
14.解:∠1与∠2互余,且∠1=35°,
则∠2=90°﹣35°=55°,
∠2的补角的度数为180°﹣55°=125°.
故填125.
15.解:∵∠1=40°,
∴∠3=90°﹣40°=50°,
∵直线l1∥l2,
∴∠2=∠3=50°.
故答案为:50°.
16.解:∵∠EAB=70°,∠DCF=60°,
∴∠BAC=110°,∠ACD=120°,
分三种情况:
如图①,AB与CD在EF的两侧时,
∠ACD=120°﹣(3t)°,∠BAC=110°﹣t°,
要使AB∥CD,则∠ACD=∠BAC,
即120°﹣(3t)°=110°﹣t°,
解得t=5;
②CD旋转到与AB都在EF的右侧时,
∠DCF=360°﹣(3t)°﹣60°=300°﹣(3t)°,∠BAC=110°﹣t°,
要使AB∥CD,则∠DCF=∠BAC,
即300°﹣(3t)°=110°﹣t°,
解得t=95;
③CD旋转到与AB都在EF的左侧时,
∠DCF=(3t)°﹣(180°﹣60°+180°)=(3t)°﹣300°,∠BAC=t°﹣110°,
要使AB∥CD,则∠DCF=∠BAC,
即(3t)°﹣300°=t°﹣110°,
解得t=95,
∴此情况不存在.
综上所述,当时间t的值为5秒或95秒时,CD与AB平行.
故答案为:5秒或95秒.
三.解答题
17.解:∵OE平分∠BOD,
∴∠BOD=2∠BOE=2×36°=72°,
∴∠AOC=∠BOD=72°.
18.解:∵∠1=∠AGH,∠1=∠2=70°,
∴∠2=∠AGH,
∴AB∥CD.
19.解:∵AB∥CD(已知),
∴∠1=∠C(两直线平行,内错角相等).
又∵∠1=70°,∠D=110°(已知),
∴∠1+∠D=180°(等式的性质).
∴∠C+∠D=180° (等量代换),
∴AC∥BD(同旁内角互补,两直线平行),
∴∠B=∠1(两直线平行,同位角相等),
∴∠B=70°,
故答案为:∠C;两直线平行,内错角相等;等量代换;AC;BD;同旁内角互补,两直线平行;∠1;两直线平行,同位角相等.
20.解:(1)设∠BOC=x,则∠AOC=2x,
依题意列方程90°﹣2x=x﹣30°,
解得:x=40°,
即∠AOC=40°×2=80°.
(2)由(1)得,∠AOC=80°,
①当射线OD在∠AOC内部时,∠AOD=16°,
则∠COD=∠AOC﹣∠AOD=80°﹣16°=64°;
②当射线OD在∠AOC外部时,∠AOD=16°,
则∠COD=∠AOC+∠AOD=80°+16°=96°.
21.(1)解:∵∠1=∠C(已知),
∴BE∥CF(同位角相等,两直线平行),
∴∠B=∠2=55°(两直线平行,同位角相等);
(2)证明:∵BE⊥DF(已知),
∴∠DPE=90°(垂直定义),
∵BE∥CF(已证),
∴∠CFD=∠DPE=90°(两直线平行,同位角相等),
∴∠2+∠BFD=180﹣∠CFD=90°(平角定义),
∵∠2+∠D=90°(已知),
∴∠BFD=∠D(同角的余角相等),
∴AB∥CD(内错角相等,两直线平行).
22.解:(1)∵∠3是∠1和∠2的“减余角”,
∴∠1+∠2﹣∠3=90°,
∴∠3=13°,
故答案为:13°.
(2)∵∠B′EC是∠AEB和∠AEB′的“减余角”,
∴∠AEB+∠AEB′﹣∠B′EC=90°,
∵∠AEB+∠AEB′+∠B′EC=180°,
∴(∠AEB+∠AEB′﹣∠B′EC)+(∠AEB+∠AEB′+∠B′EC)=90°+180°,
∴∠AEB+∠AEB′=135°,
由对折得∠AEB=∠AEB′,
∴∠AEB=67.5°.
(3)存在∠AEB,∠AEC′,∠B′EC中的一个角是其它两个角的“减余角”.
理由如下:
由对折设∠B'EC'=∠B'EC=α,
∠AEB'=β,
∴∠AEB=α+β.
当∠AEB+∠AEC′﹣∠B′EC=90°时,
α+β+β﹣α=90°,
∴β=45°,
由平角∠AEB+∠AEC'+∠B'EC'+∠B'EC=180°,
∴α+β+β+2α=180°,
∴α=30°,
∴∠AEB=α+β=75°.
当∠AEB+∠B′EC﹣∠AEC′=90°时,
α+β+α﹣β=90°,
∴α=45°,
由平角∠AEB+∠AEC'+∠B'EC'+∠B'EC=180°,
∴β=22.5°,
∴∠AEB=67.5°.
综上所述,∠AEB=75°或67.5°.
23.解:(1)∵AM∥BN,
∴∠A+∠ABN=180°,
又∵∠A=60°,
∴∠ABN=180°﹣∠A=120°.
∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBP=∠ABP,∠DBP=∠PBN,
∴∠CBD=∠CBP+∠DBP=∠ABP+∠PBN=∠ABN=60°,
∴∠CBD=∠A.
(2)∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBP=∠ABP,∠DBP=∠PBN,
∴∠CBD=∠CBP+∠DBP=∠ABP+∠PBN=∠ABN,
∵AM∥BN,
∴∠A+∠ABN=180°,
∴∠ABN=180°﹣∠A,
∴∠CBD=.
(3)∠APB=2∠ADB 理由如下:
∵BD分别平分∠PBN,
∴∠PBN=2∠NBD,
∵AM∥BN,
∴∠PBN=∠APB,∠NBD=∠ADB,
∴∠APB=2∠ADB.
(4)∵AM∥BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN,
∵BC,BD分别平分∠ABP和∠PBN,
∴2∠ABC=∠ABN,
∵AM∥BN,
∴∠A+∠ABN=180°,
∴2∠ABC+∠A=(∠A+∠ABN)=×180°=90°.
满分100分
一.选择题(共10小题,满分30分,每小题3分)
1.下列图形中,线段AD的长度表示点A到直线BC距离的是( )
A.B.C.D.
2.平面内有五条直线两两相交,设最多交点个数为a,最少交点个数为b,则a+b的值是( )
A.9 B.10 C.11 D.14
3.如图,直线AB,CD相交于点O,若射线OP平分∠AOD,射线OD平分∠BOP,则∠BOC的度数为( )
A.115° B.120° C.125° D.130°
4.两条直线被第三条直线所截,形成了常说的“三线八角”.为了便于记忆,同学们可用双手表示“三线八角”(两大拇指代表被截直线,两只食指在同一直线上代表截线),如图,它们构成的一对角可以看成( )
A.同位角 B.同旁内角 C.内错角 D.对顶角
5.如图,下列条件中,能判定AB∥CD的是( )
A.∠1=∠4 B.∠1=∠3 C.∠5=∠ADC D.∠2=∠4
6.将一副三角板(含30°,45°,60°,90°角)按如图所示的位置摆放在直尺上,则∠1的余角度数是( )
A.15° B.60° C.75° D.105°
7.如图,直线c与直线a,b都相交.若a∥b,∠1=53°,则∠2=( )
A.50° B.51° C.52° D.53°
8.如图,一束光线AB先后经平面镜OM,ON反射后,反射光线CD与AB平行,当∠ABM=35°时,∠DCB的度数是( )
A.55° B.70° C.60° D.35°
9.如图,是赛车跑道的一段示意图,其中AB∥DE,测得∠B=130°,∠D=120°,则∠C的度数为( )
A.120° B.110° C.140° D.90°
10.按如图的方法折纸,下列说法不正确的是( )
A.∠1与∠3互余 B.∠2=90°
C.AE平分∠BEF D.∠1与∠AEC互补
二.填空题(共6小题,满分18分,每小题3分)
11.如图,直线AB,CD被AE所截,则∠A的同旁内角是 .
12.如图,直线l表示一段河道,点P表示村庄,现要从河l向村庄P引水,图中有四种方案,其中沿线段PC路线开挖的水渠长最短,理由是 .
13.如图是一种对顶角量角器,它所测量的角的度数是 ,用它测量角的原理是 .
14.已知∠1与∠2互余,且∠1=35°,则∠2的补角的度数为 度.
15.如图,直线l1∥l2,将直角三角板按如图方式放置,直角顶点在l2上,若∠1=40°,则∠2= .
16.如图,直线EF上有两点A、C,分别引两条射线AB、CD,∠DCF=60°,∠EAB=70°,射线AB、CD分别绕A点,C点以1度/秒和3度/秒的速度同时顺时针转动,在射线CD转动一周的时间内,使得CD与AB平行所有满足条件的时间= .
三.解答题(共7小题,满分52分)
17.(5分)如图,直线AB、CD相交于点O,OE平分∠BOD,∠BOE=36°.求∠AOC的度数.
18.(5分)如图,直线AB、CD分别与EF相交于点G、H,已知∠1=70°,∠2=70°,试说明:AB∥CD.
19.(8分)如图,直线AB∥CD,∠1=70°,∠D=110°,求∠B的度数.
阅读下面的解答过程,并填空(理由或数学式).
解:∵AB∥CD(已知),
∴∠1=(① )(② ).
又∵∠1=70°,∠D=110°(已知),
∴∠1+∠D=180°(等式的性质).
∴∠C+∠D=180°(③ ).
∴(④ )∥(⑤ )(⑥ ).
∴∠B=(⑦ )(⑧ ).
∴∠B=70°
20.(8分)如图所示,已知∠AOC=2∠BOC,∠AOC的余角比∠BOC小30°.
(1)求∠AOC的度数;
(2)过点O作射线OD,使得∠AOC=5∠AOD,请你求出∠COD的度数.
21.(8分)如图,∠1=∠C,BE⊥DF于点P.
(1)若∠2=55°,请求出∠B的度数;
(2)若∠2+∠D=90°,求证:AB∥CD.
22.(9分)定义:如果有三个角α,β,γ,满足α+β﹣γ=90°,则称γ是α和β的“减余角”.
(1)已知∠1=37°,∠2=66°,若∠3是∠1和∠2的“减余角”,则∠3= .
(2)现有一张正方形纸片ABCD,如图1所示,点E为线段BC上一点(不与B、C重合).连结AE,将纸片沿着AE对折,使点B落在正方形纸片的内部且对应点为B′.
①若∠B′EC是∠AEB和∠AEB′的“减余角”,求∠AEB的度数.
②再将此正方形纸片沿着B′E所在直线对折,使点C落在正方形纸片的内部且对应点为C′,如图2所示.是否存在∠AEB,∠AEC′,∠B′EC中的一个角是其它两个角的“减余角”?若存在,请求出∠AEB的度数;若不存在,请说明理由.
23.(9分)综合与探究
问题情境
在综合实践课上,老师组织七年级(2)班的同学开展了探究两角之间数量关系的数学活动,如图,已知射线AM∥BN,连接AB,点P是射线AM上的一个动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
探索发现
“快乐小组”经过探索后发现:
(1)当∠A=60°时,∠CBD=∠A.请说明理由.
(2)不断改变∠A的度数,∠CBD与∠A却始终存在某种数量关系,用含∠A的式子表示∠CBD为 .
操作探究
(3)“智慧小组”利用量角器量出∠APB和∠ADB的度数后,探究二者之间的数量关系.他们惊奇地发现,当点P在射线AM上运动时,无论点P在AM上的什么位置,∠APB与∠ADB之间的数量关系都保持不变,请写出它们的关系,并说明理由.
(4)点P继续在射线AM上运动,当运动到使∠ACB=∠ABD时,请直接写出2∠ABC+∠A的结果.
参考答案
一.选择题
1.解:A.AD与BC不垂直,故线段AD的长不能表示点A到直线BC距离,不合题意.
B.AD与BC不垂直,故线段AD的长不能表示点A到直线BC距离,不合题意;
C.AD与BC不垂直,故线段AD的长不能表示点A到直线BC距离,不合题意;
D.AD⊥BC于D,则线段AD的长表示点A到直线BC的距离,符合题意;
故选:D.
2.解:平面内有五条直线两两相交,最多交点个数为a==10,最少交点个数为b=1,
∴a+b=10+1=11.
故选:C.
3.解:∵射线OP平分∠AOD,射线OD平分∠BOP,
∴∠AOP=∠POD=∠BOD,
∵∠AOP+∠POD+∠BOD=180°,
∴∠BOD=60°.
∴∠AOC=∠BOD=60°.
∵∠BOC+∠AOC=180°,
∴∠BOC=120°.
故选:B.
4.解:用双手表示“三线八角”(两大拇指代表被截直线,两只食指在同一直线上代表截线),如图,它们构成的一对角可以看成同位角.
故选:A.
5.解:A.∠1=∠4,不能判定AB∥CD,故该选项不正确,不符合题意;
B.∵∠1=∠3,∴AB∥CD,故该选项正确,符合题意;
C.∵∠5=∠ADC,∴AD∥BC,故该选项不正确,不符合题意;
D.∠2=∠4,∴AD∥BC,故该选项不正确,不符合题意;
故选:B.
6.解:如下图所示:
依题意得:∠2=45°,∠3=60°,
∴∠2+∠3=105°,
∵∠4+∠2+∠3=180°,
∴∠4=75°,
根据直尺的对边平行得∠1=∠4=75°,
∴∠1的余角为:90°﹣∠1=90°﹣75°=15°.
故选:A.
7.解:∵a∥b,
∴∠1=∠2,
∵∠1=53°,
∴∠2=53°.
故选:D.
8.解:由反射定律得到:∠OBC=∠ABM=35°,
∴∠ABC=180°﹣35°﹣35°=110°,
∵AB∥CD,
∴∠BCD+∠ABC=180°,
∴∠BCD=70°.
故选:B.
9.解:如图所示:过点C作CF∥AB.
∵AB∥DE,
∴DE∥CF;
∴∠BCF=180°﹣∠B=50°,∠DCF=180°﹣∠D=60°;
∴∠C=∠BCF+∠DCF=110°.
故选:B.
10.解:根据折叠的性质可知,∠1=∠AEB,∠3=∠FEC,
∵∠1+∠AEB+∠3+∠FEC=180°,
∴2(∠1+∠3)=180°,即∠1+∠3=90°,故A不符合题意;
∴∠2=90°,故B不符合题意,C符合题意;
∵∠1+∠AEC=180°,故D不符合题意.
故选:C.
二.填空题
11.解:∵直线AB,CD被AE所截,
∴∠A的同旁内角是∠AOC.
故答案为:∠AOC.
12.解:沿线段PC路线开挖的水渠长最短,理由是垂线段最短.
故答案为:垂线段最短.
13.解:由量角器的读数可知,所测量角的度数为30°,
原理:对顶角相等,
故答案为:30°,对顶角相等.
14.解:∠1与∠2互余,且∠1=35°,
则∠2=90°﹣35°=55°,
∠2的补角的度数为180°﹣55°=125°.
故填125.
15.解:∵∠1=40°,
∴∠3=90°﹣40°=50°,
∵直线l1∥l2,
∴∠2=∠3=50°.
故答案为:50°.
16.解:∵∠EAB=70°,∠DCF=60°,
∴∠BAC=110°,∠ACD=120°,
分三种情况:
如图①,AB与CD在EF的两侧时,
∠ACD=120°﹣(3t)°,∠BAC=110°﹣t°,
要使AB∥CD,则∠ACD=∠BAC,
即120°﹣(3t)°=110°﹣t°,
解得t=5;
②CD旋转到与AB都在EF的右侧时,
∠DCF=360°﹣(3t)°﹣60°=300°﹣(3t)°,∠BAC=110°﹣t°,
要使AB∥CD,则∠DCF=∠BAC,
即300°﹣(3t)°=110°﹣t°,
解得t=95;
③CD旋转到与AB都在EF的左侧时,
∠DCF=(3t)°﹣(180°﹣60°+180°)=(3t)°﹣300°,∠BAC=t°﹣110°,
要使AB∥CD,则∠DCF=∠BAC,
即(3t)°﹣300°=t°﹣110°,
解得t=95,
∴此情况不存在.
综上所述,当时间t的值为5秒或95秒时,CD与AB平行.
故答案为:5秒或95秒.
三.解答题
17.解:∵OE平分∠BOD,
∴∠BOD=2∠BOE=2×36°=72°,
∴∠AOC=∠BOD=72°.
18.解:∵∠1=∠AGH,∠1=∠2=70°,
∴∠2=∠AGH,
∴AB∥CD.
19.解:∵AB∥CD(已知),
∴∠1=∠C(两直线平行,内错角相等).
又∵∠1=70°,∠D=110°(已知),
∴∠1+∠D=180°(等式的性质).
∴∠C+∠D=180° (等量代换),
∴AC∥BD(同旁内角互补,两直线平行),
∴∠B=∠1(两直线平行,同位角相等),
∴∠B=70°,
故答案为:∠C;两直线平行,内错角相等;等量代换;AC;BD;同旁内角互补,两直线平行;∠1;两直线平行,同位角相等.
20.解:(1)设∠BOC=x,则∠AOC=2x,
依题意列方程90°﹣2x=x﹣30°,
解得:x=40°,
即∠AOC=40°×2=80°.
(2)由(1)得,∠AOC=80°,
①当射线OD在∠AOC内部时,∠AOD=16°,
则∠COD=∠AOC﹣∠AOD=80°﹣16°=64°;
②当射线OD在∠AOC外部时,∠AOD=16°,
则∠COD=∠AOC+∠AOD=80°+16°=96°.
21.(1)解:∵∠1=∠C(已知),
∴BE∥CF(同位角相等,两直线平行),
∴∠B=∠2=55°(两直线平行,同位角相等);
(2)证明:∵BE⊥DF(已知),
∴∠DPE=90°(垂直定义),
∵BE∥CF(已证),
∴∠CFD=∠DPE=90°(两直线平行,同位角相等),
∴∠2+∠BFD=180﹣∠CFD=90°(平角定义),
∵∠2+∠D=90°(已知),
∴∠BFD=∠D(同角的余角相等),
∴AB∥CD(内错角相等,两直线平行).
22.解:(1)∵∠3是∠1和∠2的“减余角”,
∴∠1+∠2﹣∠3=90°,
∴∠3=13°,
故答案为:13°.
(2)∵∠B′EC是∠AEB和∠AEB′的“减余角”,
∴∠AEB+∠AEB′﹣∠B′EC=90°,
∵∠AEB+∠AEB′+∠B′EC=180°,
∴(∠AEB+∠AEB′﹣∠B′EC)+(∠AEB+∠AEB′+∠B′EC)=90°+180°,
∴∠AEB+∠AEB′=135°,
由对折得∠AEB=∠AEB′,
∴∠AEB=67.5°.
(3)存在∠AEB,∠AEC′,∠B′EC中的一个角是其它两个角的“减余角”.
理由如下:
由对折设∠B'EC'=∠B'EC=α,
∠AEB'=β,
∴∠AEB=α+β.
当∠AEB+∠AEC′﹣∠B′EC=90°时,
α+β+β﹣α=90°,
∴β=45°,
由平角∠AEB+∠AEC'+∠B'EC'+∠B'EC=180°,
∴α+β+β+2α=180°,
∴α=30°,
∴∠AEB=α+β=75°.
当∠AEB+∠B′EC﹣∠AEC′=90°时,
α+β+α﹣β=90°,
∴α=45°,
由平角∠AEB+∠AEC'+∠B'EC'+∠B'EC=180°,
∴β=22.5°,
∴∠AEB=67.5°.
综上所述,∠AEB=75°或67.5°.
23.解:(1)∵AM∥BN,
∴∠A+∠ABN=180°,
又∵∠A=60°,
∴∠ABN=180°﹣∠A=120°.
∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBP=∠ABP,∠DBP=∠PBN,
∴∠CBD=∠CBP+∠DBP=∠ABP+∠PBN=∠ABN=60°,
∴∠CBD=∠A.
(2)∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBP=∠ABP,∠DBP=∠PBN,
∴∠CBD=∠CBP+∠DBP=∠ABP+∠PBN=∠ABN,
∵AM∥BN,
∴∠A+∠ABN=180°,
∴∠ABN=180°﹣∠A,
∴∠CBD=.
(3)∠APB=2∠ADB 理由如下:
∵BD分别平分∠PBN,
∴∠PBN=2∠NBD,
∵AM∥BN,
∴∠PBN=∠APB,∠NBD=∠ADB,
∴∠APB=2∠ADB.
(4)∵AM∥BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN,
∵BC,BD分别平分∠ABP和∠PBN,
∴2∠ABC=∠ABN,
∵AM∥BN,
∴∠A+∠ABN=180°,
∴2∠ABC+∠A=(∠A+∠ABN)=×180°=90°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
