苏科版八年级上册数学第2章《轴对称图形》单元测试卷(基础卷)(含解析)
文档属性
| 名称 | 苏科版八年级上册数学第2章《轴对称图形》单元测试卷(基础卷)(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 10:05:03 | ||
图片预览


文档简介
第2章 轴对称图形(基础卷)
一、选择题(每小题3分,共18分)
1.2022年冬奥会在北京举行,以下历届冬奥会会徽是轴对称图形的是( )
A. B. C. D.
2.如图,将一张长方形纸片ABCD沿EF折叠,点A、B分别落在点、处,若,则的度数是( )
A.65° B.60° C.50° D.57.5°
3.如图,在网格图中选择一个格子涂阴影,使得整个图形是以虚线为对称轴的轴对称图形.则这个格子内标有的数字是( )
A.1 B.2 C.3 D.4
4.如图,在△ABC中,cm,线段AB的垂直平分线交AC于点N,△BCN的周长是13cm,则BC的长为( )
A.6cm B.7cm C.8cm D.13cm
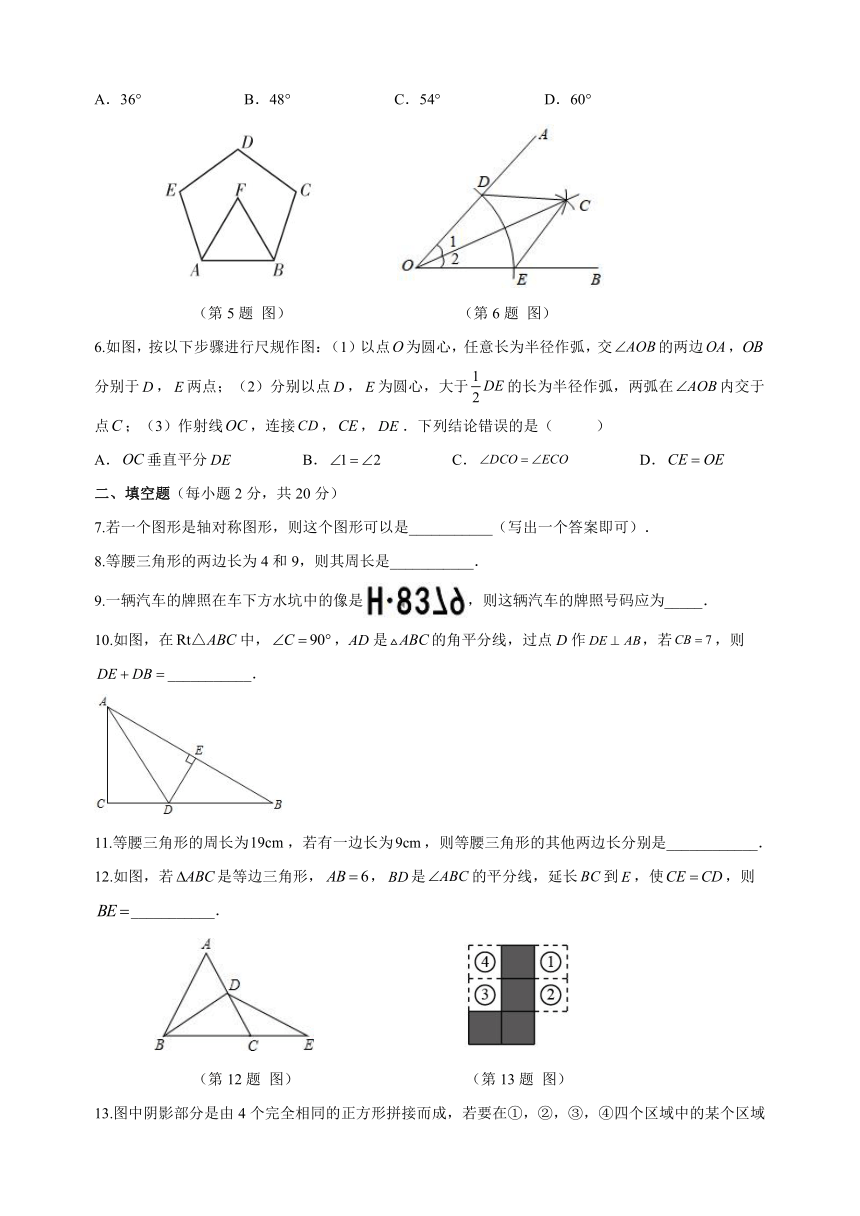
5.如图,点在正五边形的内部,为等边三角形,则等于( )
A.36° B.48° C.54° D.60°
(第5题 图) (第6题 图)
6.如图,按以下步骤进行尺规作图:(1)以点为圆心,任意长为半径作弧,交的两边,分别于,两点;(2)分别以点,为圆心,大于的长为半径作弧,两弧在内交于点;(3)作射线,连接,,.下列结论错误的是( )
A.垂直平分 B. C. D.
二、填空题(每小题2分,共20分)
7.若一个图形是轴对称图形,则这个图形可以是___________(写出一个答案即可).
8.等腰三角形的两边长为4和9,则其周长是___________.
9.一辆汽车的牌照在车下方水坑中的像是,则这辆汽车的牌照号码应为_____.
10.如图,在中,,AD是的角平分线,过点D作,若,则___________.
11.等腰三角形的周长为,若有一边长为,则等腰三角形的其他两边长分别是____________.
12.如图,若是等边三角形,,是的平分线,延长到,使,则___________.
(第12题 图) (第13题 图)
13.图中阴影部分是由4个完全相同的正方形拼接而成,若要在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是轴对称图形,则这个正方形应该添加在区域___________.(填序号)
14.如图,在中,,点在延长线上,于点,交于点,若,,则的长度为___________.
(第14题 图) (第15题 图)
15.如图,在中,,是的角平分线,若,,则的面积是__________.
16.已知在中,,,,点E为边上的动点,点F为边上的动点,则线段的最小值是_______________.
三、解答题(共62分)
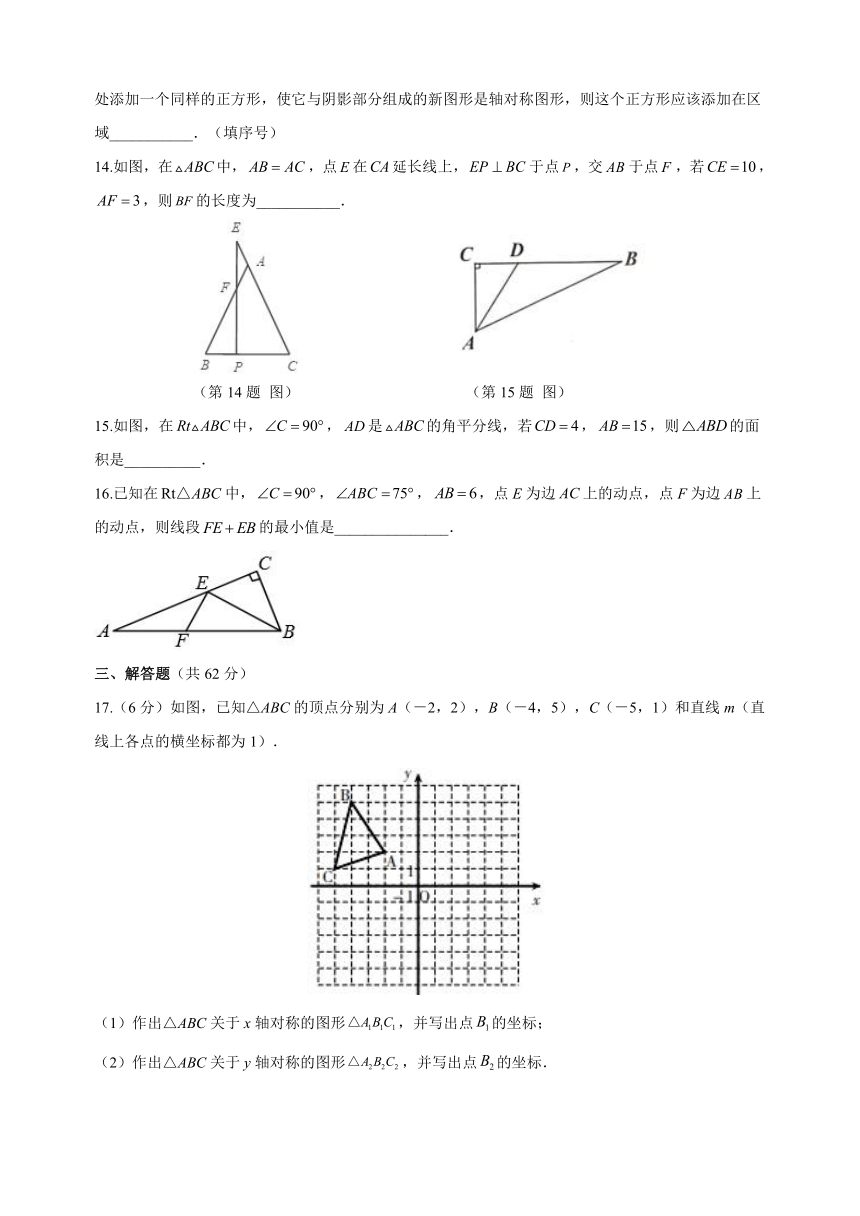
17.(6分)如图,已知△ABC的顶点分别为A(-2,2),B(-4,5),C(-5,1)和直线m(直线上各点的横坐标都为1).
(1)作出△ABC关于x轴对称的图形,并写出点的坐标;
(2)作出△ABC关于y轴对称的图形,并写出点的坐标.
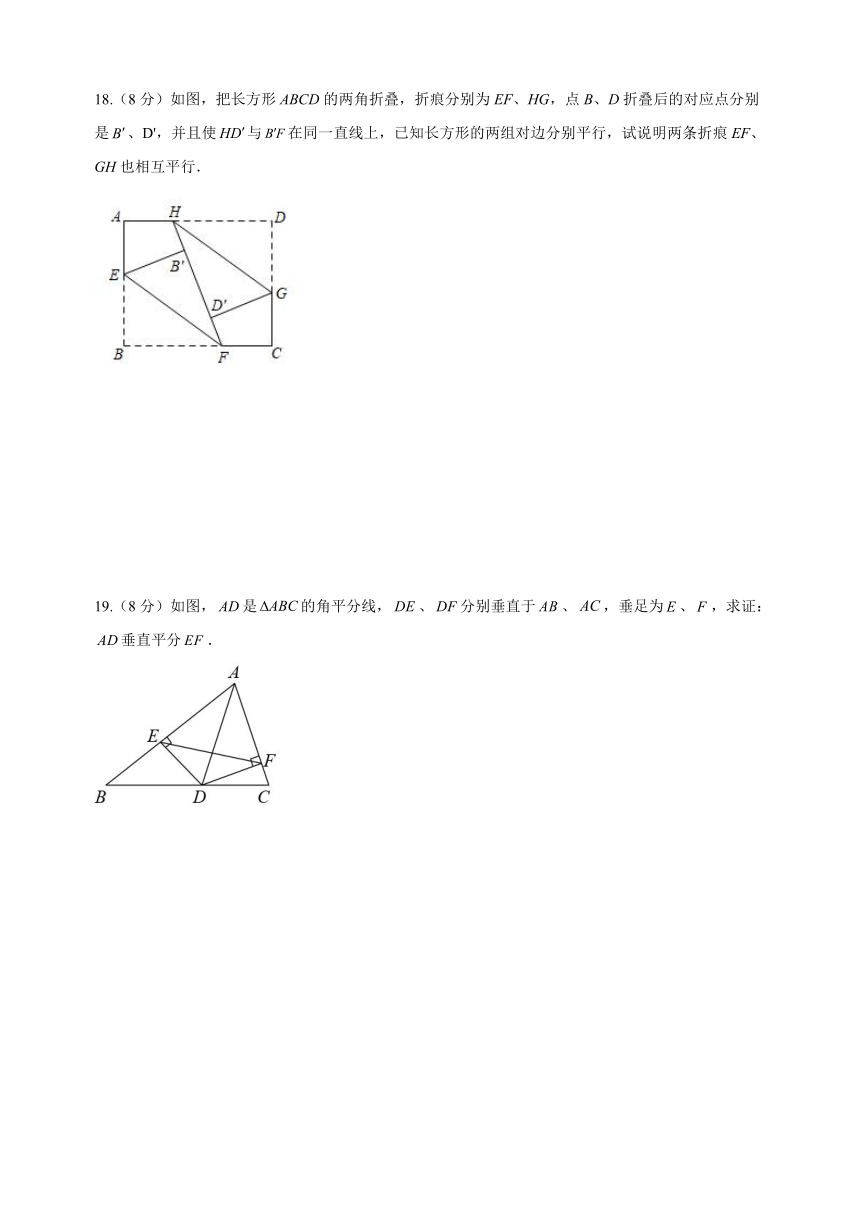
18.(8分)如图,把长方形ABCD的两角折叠,折痕分别为EF、HG,点B、D折叠后的对应点分别是、D',并且使与在同一直线上,已知长方形的两组对边分别平行,试说明两条折痕EF、GH也相互平行.
19.(8分)如图,是的角平分线,、分别垂直于、,垂足为、,求证:垂直平分.
20.(10分)如图,在中,的平分线与的外角的平分线交于点,于点,,交的延长线于点.
(1)若点到直线的距离为5cm,求点到直线的距离;
(2)求证:点在的平分线上.
21.(10分)如图,BD是△ABC中AC边上的中线,过点C作,交BD的延长线于点E,F为△ABC外一点,连接CF、DF,且DE=DF、∠ADF=∠CDE.求证:
(1)△ABD≌△CED;
(2)CA平分∠BCF.
22.(10分)如图所示,点E,F在BC上且.
(1)求证:;
(2)若PO平分,则PO与线段BC有什么关系 为什么
23.(10分)如图(1),在中,的平分线交边于点D.
(1)求证:为等腰三角形;
(2)若的平分线交边于点E,如图(2),求证:;
(3)若外角的平分线交的延长线于点E,请你探究(2)中的结论是否仍然成立,若不成立,请写出正确的结论,并说明理由.
参考答案
一、选择题(每小题3分,共18分)
1、B
【解析】解:选项A、C、D不能找到这样一条直线使图形沿着一条直线折叠,直线旁的两个部分能够互相重合,所以不是轴对称图形;
选项B能能找到这样一条直线使图形沿着一条直线折叠,直线旁的两个部分能够互相重合,所以是轴对称图形.
故选B.
2、C
【解析】解:由折叠可得,∠1=∠A'EF=65°,
∴∠AEA'=130°,
∴∠A'ED=180°-130°=50°,
故选:C.
3、C
【解析】解:由轴对称图形的定义可知,这个格子内标有的数字是3,
故选:C.
4、B
【解析】解:线段的垂直平分线交于点,
,
,
又的周长是,
,
故选:B.
5、B
【解析】∵五边形ABCDE是正五边形,
∴ ,
∵△ABF为等边三角形,
∴,
∴,
故选:B.
6、D
【解析】解:由作图可知,在△OCD和△OCE中,
,
∴△OCD≌△OCE(SSS),∴∠DCO=∠ECO,∠1=∠2,
∵OD=OE,CD=CE,∴OC垂直平分线段DE,
故A,B,C正确,
没有条件能证明CE=OE,
故选:D.
二、填空题(每小题2分,共20分)
7、圆(答案不唯一)
【解析】解:若一个图形是轴对称图形,则这个图形可以是圆.
故答案为:圆(答案不唯一).
8、22
【解析】解:①当4为腰时,边长为4、4、9, 4+4<9,不能构成三角形,舍去;
②当9为腰时,边长为4、9、9, 能构成三角形,此时三角形的周长为.
故答案为22.
9、H 8379
【解析】解:如图所示:
该车牌照号码为:H 8379.
故答案为:H 8379.
10、7
【解析】解:∵AD平分∠BAC交BC于点D,,DE⊥AB,∴CD=ED.
∵,∴BD+CD=7,∴,
故答案为:7.
11、9cm、1cm或5cm、5cm.
【解析】解:①当9cm为腰长时,则腰长为9cm,底边=19-9-9=1cm,因为9+1>9,
所以能构成三角形;
②当9cm为底边时,则腰长=(19-9)÷2=5cm,因为5+5>9,所以能构成三角形.
则等腰三角形其他两边长分别为9cm、1cm或5cm、5cm.
故答案为:9cm、1cm或5cm、5cm.
12、9
【解析】证明:是等边三角形,
,BD是的平分线,
,,
,,
.
故答案为:9.
13、④
【解析】解:如图所示,在④处添加一个同样的正方形,使它与阴影部分组成的新图形是轴对称图形,
故答案为:④.
14、4
【解析】证明:在△ABC中,
∵AB=AC,∴∠B=∠C,
∵EP⊥BC,∴∠C+∠E=90°,∠B+∠BFP=90°,∴∠E=∠BFP,
又∵∠BFP=∠AFE,∴∠E=∠AFE,∴AF=AE=3,∴△AEF是等腰三角形.
又∵CE=10,∴CA=AB=7,∴BF=AB-AF=7-3=4,
故答案为:4.
15、30
【解析】解:如图,作于H.
平分,,,,
,
故答案为30.
16、3
【解析】解:如图,作点关于的对称点,连接,
,,
由两点之间线段最短可知,当点共线时,最小,最小值为,
由垂线段最短可知,当时,的值最小,
,,
又,(等腰三角形的三线合一),
,
则在中,,
即的最小值为3,
故答案为:3.
三、解答题(共62分)
17.
(1)图见解析,点的坐标为(-4,-5);(2)图见解析,点的坐标为(4,5)
【解析】解:(1)如图所示,即为所求作的三角形,点的坐标为(-4,-5).
(2)如图所示,即为所求作的三角形,点的坐标为(4,5).
18.
【答案】见解析
【解析】证明:根据折叠可知,,,
∵长方形的两组对边分别平行,即
∴,
∵,,
∴,
∴.
19.
【答案】见解析
【解析】证明:是的角平分线,,,,
在和中,
,
,,
又,
垂直平分到线段两端点的距离相等的点一定在线段的垂直平分线上
20.
(1)5cm;(2)见解析.
【解析】(1)解:过点作于,
点在的平分线,,,
cm,
即点到直线的距离为;
(2)证明:点在的平分线,,,,
同理:,,
,,
点在的平分线上.
21.
(1)证明见解析;(2)证明见解析
【解析】(1)证明:∵,
∴∠ABD=∠CED,∠BAD=∠DCE,
∵BD是△ABC中AC边上的中线,∴AD=CD,
在△ABD和△CED中,
∵,
∴△ABD≌△CED(AAS).
(2)证明:∵△ABD≌△CED,∴BD=DE,∠ADB=∠CDE,
又∵DE=DF,∴BD=DF,
∵∠ADF=∠CDE,∠CDE=∠ADB,∴∠ADB=∠ADF,
∴,∴∠BDC=∠FDC,
在△BDC和△FDC中,
∵,
∴△BDC≌△FDC(SAS),∴∠BCD=∠FCD,∴CA平分∠BCF.
22.
(1)见详解;(2)PO垂直平分BC;理由见详解
【解析】(1)证明:∵BE=CF,BC=CB,∴BF=CE,
在Rt△ABF与Rt△DCE中,
∵∴Rt△ABF≌Rt△DCE(HL),∴;
(2)解:PO垂直平分BC,
∵Rt△ABF≌Rt△DCE,∴∠E=∠F,∴△PEF为等腰三角形,
又∵PO平分∠EPF,
∴PO⊥BC(三线合一),EO=FO(三线合一),
又∵EB=FC,∴BO=CO,∴PO垂直平分BC.
23.
(1)见解析;(2)见解析;(3)不成立,正确结论:,理由见解析
【解析】(1)【证明】在中,,,
∴.
∵平分,∴,∴,∴,
∴为等腰三角形.
(2)【证明】如图(1),在AC上截取,连接.
由(1)得为等腰三角形,∴,∴.
∵平分,∴,∴,
∴,∴,
∴,∴,∴,∴.
(3)【解】不成立,正确结论:.
理由:如图(2),在上截取,连接.
∵由(1)得,∴.
∵,∴.
∵平分,∴,
∴,,∴,则.
∵,∴,
∴,
∴.
一、选择题(每小题3分,共18分)
1.2022年冬奥会在北京举行,以下历届冬奥会会徽是轴对称图形的是( )
A. B. C. D.
2.如图,将一张长方形纸片ABCD沿EF折叠,点A、B分别落在点、处,若,则的度数是( )
A.65° B.60° C.50° D.57.5°
3.如图,在网格图中选择一个格子涂阴影,使得整个图形是以虚线为对称轴的轴对称图形.则这个格子内标有的数字是( )
A.1 B.2 C.3 D.4
4.如图,在△ABC中,cm,线段AB的垂直平分线交AC于点N,△BCN的周长是13cm,则BC的长为( )
A.6cm B.7cm C.8cm D.13cm
5.如图,点在正五边形的内部,为等边三角形,则等于( )
A.36° B.48° C.54° D.60°
(第5题 图) (第6题 图)
6.如图,按以下步骤进行尺规作图:(1)以点为圆心,任意长为半径作弧,交的两边,分别于,两点;(2)分别以点,为圆心,大于的长为半径作弧,两弧在内交于点;(3)作射线,连接,,.下列结论错误的是( )
A.垂直平分 B. C. D.
二、填空题(每小题2分,共20分)
7.若一个图形是轴对称图形,则这个图形可以是___________(写出一个答案即可).
8.等腰三角形的两边长为4和9,则其周长是___________.
9.一辆汽车的牌照在车下方水坑中的像是,则这辆汽车的牌照号码应为_____.
10.如图,在中,,AD是的角平分线,过点D作,若,则___________.
11.等腰三角形的周长为,若有一边长为,则等腰三角形的其他两边长分别是____________.
12.如图,若是等边三角形,,是的平分线,延长到,使,则___________.
(第12题 图) (第13题 图)
13.图中阴影部分是由4个完全相同的正方形拼接而成,若要在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是轴对称图形,则这个正方形应该添加在区域___________.(填序号)
14.如图,在中,,点在延长线上,于点,交于点,若,,则的长度为___________.
(第14题 图) (第15题 图)
15.如图,在中,,是的角平分线,若,,则的面积是__________.
16.已知在中,,,,点E为边上的动点,点F为边上的动点,则线段的最小值是_______________.
三、解答题(共62分)
17.(6分)如图,已知△ABC的顶点分别为A(-2,2),B(-4,5),C(-5,1)和直线m(直线上各点的横坐标都为1).
(1)作出△ABC关于x轴对称的图形,并写出点的坐标;
(2)作出△ABC关于y轴对称的图形,并写出点的坐标.
18.(8分)如图,把长方形ABCD的两角折叠,折痕分别为EF、HG,点B、D折叠后的对应点分别是、D',并且使与在同一直线上,已知长方形的两组对边分别平行,试说明两条折痕EF、GH也相互平行.
19.(8分)如图,是的角平分线,、分别垂直于、,垂足为、,求证:垂直平分.
20.(10分)如图,在中,的平分线与的外角的平分线交于点,于点,,交的延长线于点.
(1)若点到直线的距离为5cm,求点到直线的距离;
(2)求证:点在的平分线上.
21.(10分)如图,BD是△ABC中AC边上的中线,过点C作,交BD的延长线于点E,F为△ABC外一点,连接CF、DF,且DE=DF、∠ADF=∠CDE.求证:
(1)△ABD≌△CED;
(2)CA平分∠BCF.
22.(10分)如图所示,点E,F在BC上且.
(1)求证:;
(2)若PO平分,则PO与线段BC有什么关系 为什么
23.(10分)如图(1),在中,的平分线交边于点D.
(1)求证:为等腰三角形;
(2)若的平分线交边于点E,如图(2),求证:;
(3)若外角的平分线交的延长线于点E,请你探究(2)中的结论是否仍然成立,若不成立,请写出正确的结论,并说明理由.
参考答案
一、选择题(每小题3分,共18分)
1、B
【解析】解:选项A、C、D不能找到这样一条直线使图形沿着一条直线折叠,直线旁的两个部分能够互相重合,所以不是轴对称图形;
选项B能能找到这样一条直线使图形沿着一条直线折叠,直线旁的两个部分能够互相重合,所以是轴对称图形.
故选B.
2、C
【解析】解:由折叠可得,∠1=∠A'EF=65°,
∴∠AEA'=130°,
∴∠A'ED=180°-130°=50°,
故选:C.
3、C
【解析】解:由轴对称图形的定义可知,这个格子内标有的数字是3,
故选:C.
4、B
【解析】解:线段的垂直平分线交于点,
,
,
又的周长是,
,
故选:B.
5、B
【解析】∵五边形ABCDE是正五边形,
∴ ,
∵△ABF为等边三角形,
∴,
∴,
故选:B.
6、D
【解析】解:由作图可知,在△OCD和△OCE中,
,
∴△OCD≌△OCE(SSS),∴∠DCO=∠ECO,∠1=∠2,
∵OD=OE,CD=CE,∴OC垂直平分线段DE,
故A,B,C正确,
没有条件能证明CE=OE,
故选:D.
二、填空题(每小题2分,共20分)
7、圆(答案不唯一)
【解析】解:若一个图形是轴对称图形,则这个图形可以是圆.
故答案为:圆(答案不唯一).
8、22
【解析】解:①当4为腰时,边长为4、4、9, 4+4<9,不能构成三角形,舍去;
②当9为腰时,边长为4、9、9, 能构成三角形,此时三角形的周长为.
故答案为22.
9、H 8379
【解析】解:如图所示:
该车牌照号码为:H 8379.
故答案为:H 8379.
10、7
【解析】解:∵AD平分∠BAC交BC于点D,,DE⊥AB,∴CD=ED.
∵,∴BD+CD=7,∴,
故答案为:7.
11、9cm、1cm或5cm、5cm.
【解析】解:①当9cm为腰长时,则腰长为9cm,底边=19-9-9=1cm,因为9+1>9,
所以能构成三角形;
②当9cm为底边时,则腰长=(19-9)÷2=5cm,因为5+5>9,所以能构成三角形.
则等腰三角形其他两边长分别为9cm、1cm或5cm、5cm.
故答案为:9cm、1cm或5cm、5cm.
12、9
【解析】证明:是等边三角形,
,BD是的平分线,
,,
,,
.
故答案为:9.
13、④
【解析】解:如图所示,在④处添加一个同样的正方形,使它与阴影部分组成的新图形是轴对称图形,
故答案为:④.
14、4
【解析】证明:在△ABC中,
∵AB=AC,∴∠B=∠C,
∵EP⊥BC,∴∠C+∠E=90°,∠B+∠BFP=90°,∴∠E=∠BFP,
又∵∠BFP=∠AFE,∴∠E=∠AFE,∴AF=AE=3,∴△AEF是等腰三角形.
又∵CE=10,∴CA=AB=7,∴BF=AB-AF=7-3=4,
故答案为:4.
15、30
【解析】解:如图,作于H.
平分,,,,
,
故答案为30.
16、3
【解析】解:如图,作点关于的对称点,连接,
,,
由两点之间线段最短可知,当点共线时,最小,最小值为,
由垂线段最短可知,当时,的值最小,
,,
又,(等腰三角形的三线合一),
,
则在中,,
即的最小值为3,
故答案为:3.
三、解答题(共62分)
17.
(1)图见解析,点的坐标为(-4,-5);(2)图见解析,点的坐标为(4,5)
【解析】解:(1)如图所示,即为所求作的三角形,点的坐标为(-4,-5).
(2)如图所示,即为所求作的三角形,点的坐标为(4,5).
18.
【答案】见解析
【解析】证明:根据折叠可知,,,
∵长方形的两组对边分别平行,即
∴,
∵,,
∴,
∴.
19.
【答案】见解析
【解析】证明:是的角平分线,,,,
在和中,
,
,,
又,
垂直平分到线段两端点的距离相等的点一定在线段的垂直平分线上
20.
(1)5cm;(2)见解析.
【解析】(1)解:过点作于,
点在的平分线,,,
cm,
即点到直线的距离为;
(2)证明:点在的平分线,,,,
同理:,,
,,
点在的平分线上.
21.
(1)证明见解析;(2)证明见解析
【解析】(1)证明:∵,
∴∠ABD=∠CED,∠BAD=∠DCE,
∵BD是△ABC中AC边上的中线,∴AD=CD,
在△ABD和△CED中,
∵,
∴△ABD≌△CED(AAS).
(2)证明:∵△ABD≌△CED,∴BD=DE,∠ADB=∠CDE,
又∵DE=DF,∴BD=DF,
∵∠ADF=∠CDE,∠CDE=∠ADB,∴∠ADB=∠ADF,
∴,∴∠BDC=∠FDC,
在△BDC和△FDC中,
∵,
∴△BDC≌△FDC(SAS),∴∠BCD=∠FCD,∴CA平分∠BCF.
22.
(1)见详解;(2)PO垂直平分BC;理由见详解
【解析】(1)证明:∵BE=CF,BC=CB,∴BF=CE,
在Rt△ABF与Rt△DCE中,
∵∴Rt△ABF≌Rt△DCE(HL),∴;
(2)解:PO垂直平分BC,
∵Rt△ABF≌Rt△DCE,∴∠E=∠F,∴△PEF为等腰三角形,
又∵PO平分∠EPF,
∴PO⊥BC(三线合一),EO=FO(三线合一),
又∵EB=FC,∴BO=CO,∴PO垂直平分BC.
23.
(1)见解析;(2)见解析;(3)不成立,正确结论:,理由见解析
【解析】(1)【证明】在中,,,
∴.
∵平分,∴,∴,∴,
∴为等腰三角形.
(2)【证明】如图(1),在AC上截取,连接.
由(1)得为等腰三角形,∴,∴.
∵平分,∴,∴,
∴,∴,
∴,∴,∴,∴.
(3)【解】不成立,正确结论:.
理由:如图(2),在上截取,连接.
∵由(1)得,∴.
∵,∴.
∵平分,∴,
∴,,∴,则.
∵,∴,
∴,
∴.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
