五年级下册数学人教版第11课时 不规则物体的体积 (课件)(共12张PPT)
文档属性
| 名称 | 五年级下册数学人教版第11课时 不规则物体的体积 (课件)(共12张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 12:49:16 | ||
图片预览




文档简介
(共12张PPT)
第11课时
不规则物体的体积
RJ 五年级下册
3 长方体和正方体
共12页 第 1 页
1、物体所占空间的大小叫做物体的( )。
体积
长方体的体积=
长×宽×高
V=a b h
正方体的体积=
棱长×棱长×棱长
V=a3
2、下面是一台微波炉。
外形尺寸:480mm×250mm×360mm
内腔尺寸:
420mm×240mm×250mm
这个微波炉的容积是多少升?
4.2×2.4×2.5=25.2(dm3 ) 25.2dm3 =25.2L
答:这个微波炉的容积是25.2升。
420mm=4.2dm 240mm=2.4dm 250mm=2.5dm
共12页 第 2 页
设法求出下面两种物体的体积。
现实生活中还有许多像橡皮泥、土豆、石块等形状不规则的物体,怎样求得它们的体积呢?
阅读与理解
要解决什么问题?这些物体分别有什么特点?
共12页 第 3 页
不能改变形状的土豆 怎么办呢?
提示:
橡皮泥捏压成规则的长方体或正方体形状,形状发生了变化,但是所占的空间大小是不变化的,这就是“等积变形”。
分析与解答
共12页 第 4 页
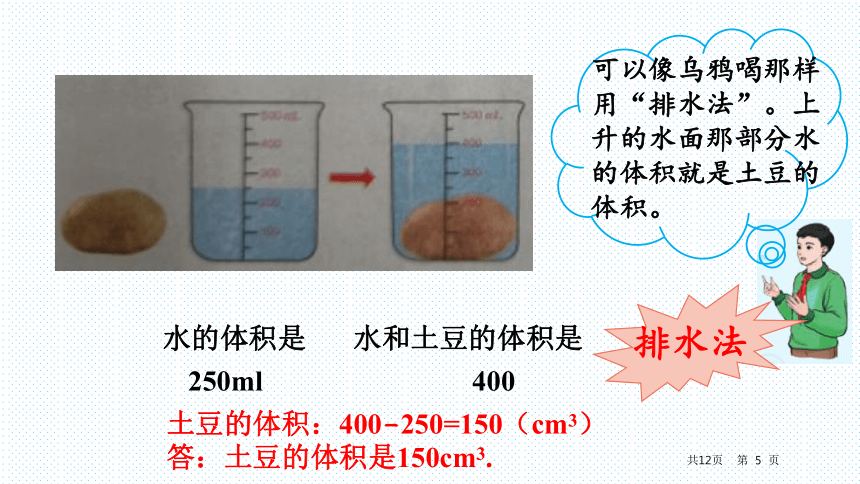
橡皮泥可以改变形状。
可以把橡皮泥捏压成规则的长方体或正方体形状,再……
250ml
400
土豆的体积:400-250=150(cm3)
答:土豆的体积是150cm3.
可以像乌鸦喝那样用“排水法”。上升的水面那部分水的体积就是土豆的体积。
排水法
共12页 第 5 页
水的体积是
水和土豆的体积是
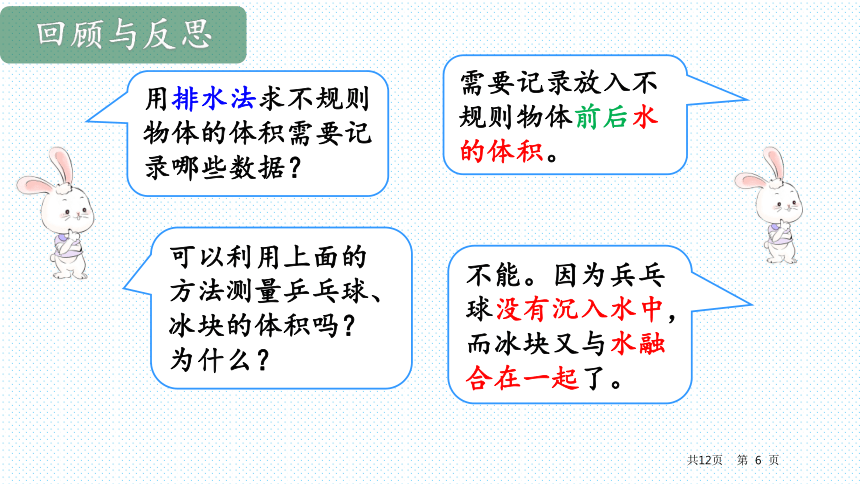
用排水法求不规则物体的体积需要记录哪些数据?
需要记录放入不规则物体前后水的体积。
可以利用上面的方法测量乒乓球、冰块的体积吗?为什么?
不能。因为兵乓球没有沉入水中,而冰块又与水融合在一起了。
回顾与反思
共12页 第 6 页
1.如图所示,你能算出这个西红柿的体积吗?
水面上升的那部分水的体积就是西红柿的体积。
答:这个西红柿的体积是300cm 。
15×10×(12-10)=300(cm )
共12页 第 7 页
2.判断:用长方体容器测算不规则物体的体积,用容器底面积乘
上升后水的高度,就是所测物体的体积。 ( )
不规则物体的体积=容器的底面积×水面上升的高度
×
水的上升高度
3.将一些水倒入一个长6分米、宽3分米、高4分米的长方体玻璃容器中,此时水深2分米,把一个石块放入水中,完全浸没后,水深变为3分米。求这个石块的体积。
6×3×(3-2)=18(立方分米)
答:这个石块的体积是18立方分米。
不规则物体的体积=容器的底面积×水面上升的高度
共12页 第 8 页
4.珊瑚石的体积是多少?
8cm
8cm
6cm
8cm
8cm
7cm
8×8×(7-6)=64(cm3)
答:珊瑚石的体积是64cm3。
5. 在一个长8m、宽5m、高2m的水池中注满水,然后把两条长3m、宽2m、高4m的石柱立着放入池中,水池溢出的水的体积是多少?
3×2×2×2=24(m3)
答:水池溢出的水的体积是24立方米。
共12页 第 9 页
6.爸爸在一个底面积为51dm 的长方体鱼缸里放了一个假山石,水面上升了3cm。这个假山石的体积有多大?
3 cm=0.3 dm
51×0.3=15.3(dm3)
答:这个假山石的体积有15.3立方分米。
7.求下图中大圆球的体积。
24 mL=24 cm3 12 mL=12 cm3
小圆球的体积:(24-12)÷3=4(cm3)
大圆球的体积:12-4=8(cm3)
12mL
24mL
共12页 第 10 页
这节课你们都学会了哪些知识?
测量不规则物体的体积,通常采用排水法,即利用有刻度的量筒或量杯,记录下放入不规则物体前后水位的刻度,上升的那部分水的体积就是不规则物体的体积。
共12页 第 11 页
作 业 请完成教材第41页练习九第6、10、11、12题。
补充作业
1、在一个长7 dm、宽5 dm、高4 dm的长方体玻璃缸中,水深
3.8 dm。把一个实心铁球完全放入水中,水溢出了7.5 dm3。
求这个铁球的体积。
共12页 第 12 页
第11课时
不规则物体的体积
RJ 五年级下册
3 长方体和正方体
共12页 第 1 页
1、物体所占空间的大小叫做物体的( )。
体积
长方体的体积=
长×宽×高
V=a b h
正方体的体积=
棱长×棱长×棱长
V=a3
2、下面是一台微波炉。
外形尺寸:480mm×250mm×360mm
内腔尺寸:
420mm×240mm×250mm
这个微波炉的容积是多少升?
4.2×2.4×2.5=25.2(dm3 ) 25.2dm3 =25.2L
答:这个微波炉的容积是25.2升。
420mm=4.2dm 240mm=2.4dm 250mm=2.5dm
共12页 第 2 页
设法求出下面两种物体的体积。
现实生活中还有许多像橡皮泥、土豆、石块等形状不规则的物体,怎样求得它们的体积呢?
阅读与理解
要解决什么问题?这些物体分别有什么特点?
共12页 第 3 页
不能改变形状的土豆 怎么办呢?
提示:
橡皮泥捏压成规则的长方体或正方体形状,形状发生了变化,但是所占的空间大小是不变化的,这就是“等积变形”。
分析与解答
共12页 第 4 页
橡皮泥可以改变形状。
可以把橡皮泥捏压成规则的长方体或正方体形状,再……
250ml
400
土豆的体积:400-250=150(cm3)
答:土豆的体积是150cm3.
可以像乌鸦喝那样用“排水法”。上升的水面那部分水的体积就是土豆的体积。
排水法
共12页 第 5 页
水的体积是
水和土豆的体积是
用排水法求不规则物体的体积需要记录哪些数据?
需要记录放入不规则物体前后水的体积。
可以利用上面的方法测量乒乓球、冰块的体积吗?为什么?
不能。因为兵乓球没有沉入水中,而冰块又与水融合在一起了。
回顾与反思
共12页 第 6 页
1.如图所示,你能算出这个西红柿的体积吗?
水面上升的那部分水的体积就是西红柿的体积。
答:这个西红柿的体积是300cm 。
15×10×(12-10)=300(cm )
共12页 第 7 页
2.判断:用长方体容器测算不规则物体的体积,用容器底面积乘
上升后水的高度,就是所测物体的体积。 ( )
不规则物体的体积=容器的底面积×水面上升的高度
×
水的上升高度
3.将一些水倒入一个长6分米、宽3分米、高4分米的长方体玻璃容器中,此时水深2分米,把一个石块放入水中,完全浸没后,水深变为3分米。求这个石块的体积。
6×3×(3-2)=18(立方分米)
答:这个石块的体积是18立方分米。
不规则物体的体积=容器的底面积×水面上升的高度
共12页 第 8 页
4.珊瑚石的体积是多少?
8cm
8cm
6cm
8cm
8cm
7cm
8×8×(7-6)=64(cm3)
答:珊瑚石的体积是64cm3。
5. 在一个长8m、宽5m、高2m的水池中注满水,然后把两条长3m、宽2m、高4m的石柱立着放入池中,水池溢出的水的体积是多少?
3×2×2×2=24(m3)
答:水池溢出的水的体积是24立方米。
共12页 第 9 页
6.爸爸在一个底面积为51dm 的长方体鱼缸里放了一个假山石,水面上升了3cm。这个假山石的体积有多大?
3 cm=0.3 dm
51×0.3=15.3(dm3)
答:这个假山石的体积有15.3立方分米。
7.求下图中大圆球的体积。
24 mL=24 cm3 12 mL=12 cm3
小圆球的体积:(24-12)÷3=4(cm3)
大圆球的体积:12-4=8(cm3)
12mL
24mL
共12页 第 10 页
这节课你们都学会了哪些知识?
测量不规则物体的体积,通常采用排水法,即利用有刻度的量筒或量杯,记录下放入不规则物体前后水位的刻度,上升的那部分水的体积就是不规则物体的体积。
共12页 第 11 页
作 业 请完成教材第41页练习九第6、10、11、12题。
补充作业
1、在一个长7 dm、宽5 dm、高4 dm的长方体玻璃缸中,水深
3.8 dm。把一个实心铁球完全放入水中,水溢出了7.5 dm3。
求这个铁球的体积。
共12页 第 12 页
