2024年高中数学教学课件★★3.1函数概念 起始课课件(共34张PPT)
文档属性
| 名称 | 2024年高中数学教学课件★★3.1函数概念 起始课课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 00:00:00 | ||
图片预览







文档简介
(共34张PPT)
人教A版《普通高中课程标准教科书 数学》必修第一册
函数概念起始课
2024年高中数学教学课件★★
环节一 创设情境“话”函数
根据短片,你能从中发现哪些函数关系?
环节一 创设情境“话”函数
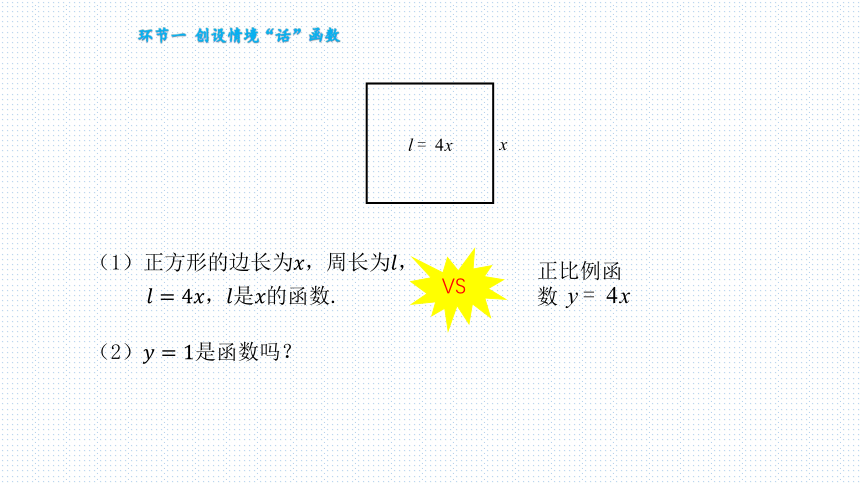
(1)正方形的边长为,周长为
(2)
的函数.
正比例函数
VS
环节一 创设情境“话”函数
问题
情境
某“复兴号”高速列车加速到350km/h后保持匀速运行半小时.
(1)列车行进的路程S与运行时间t的关系是什么?
(2)你能用初中所学函数概念描述S与t的函数关系吗?
(3)有人说:“根据对应关系这趟列车加速到350km/h后, 运行1h就前进了350km.”你认为这个说法正确吗?
(4)如何用更精确的语言来描述S与t的函数关系呢?
(4)如何用更精确的语言来描述S与t的函数关系呢?
新教材在第一章《集合与常用逻辑用语》章引言曾讲到集合的作用:为了简洁、准确地表述数学对象及研究范围,我们需要使用集合的语言和工具.
环节一 创设情境“话”函数
环节一 创设情境“话”函数
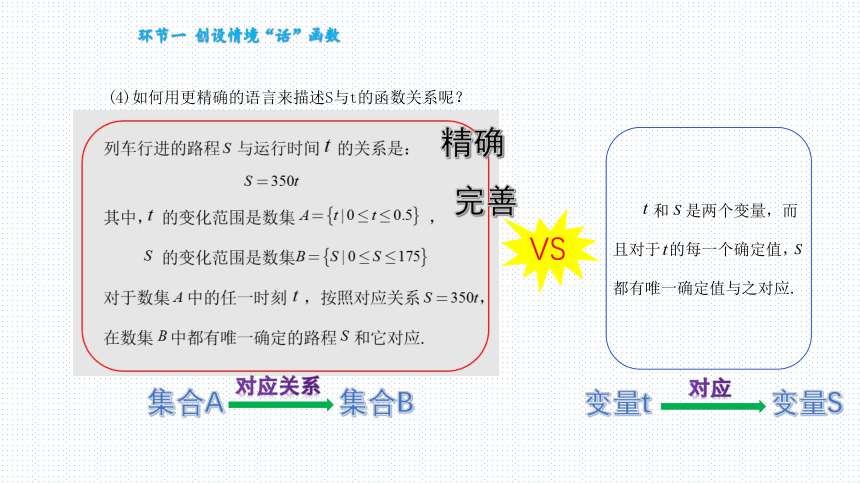
(4)如何用更精确的语言来描述S与t的函数关系呢?
VS
和 是两个变量,而
且对于 的每一个确定值,
都有唯一确定值与之对应.
集合A
集合B
对应关系
变量t
变量S
对应
精确
完善
活动一
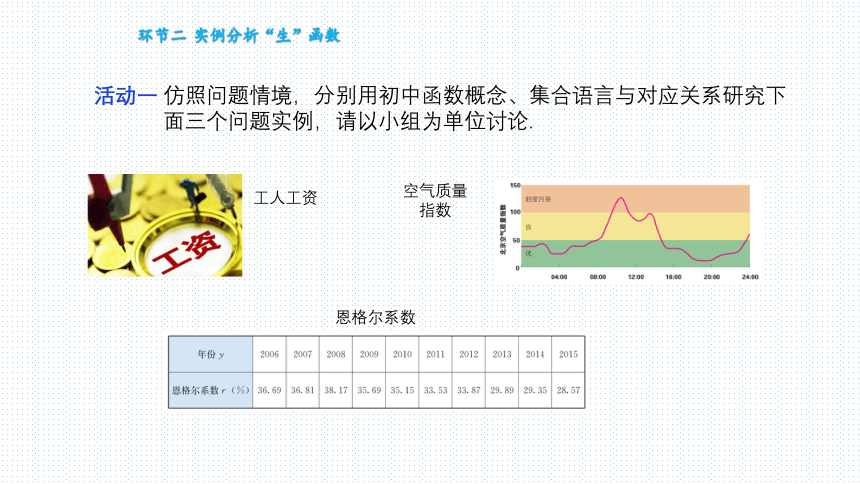
仿照问题情境,分别用初中函数概念、集合语言与对应关系研究下面三个问题实例,请以小组为单位讨论.
工人工资
空气质量指数
恩格尔系数
环节二 实例分析“生”函数
活动二
VS
集合-对应
“变量说”
对比发现,自我点评两种刻画函数的方法.
环节二 实例分析“生”函数
关于数学概念的生成,本书主编,人教社章建跃博士曾说:“数学的概念应该怎么获得?可以从大量同类事物的不同例证中找到它们的共同的关键特征. ”
环节二 实例分析“生”函数
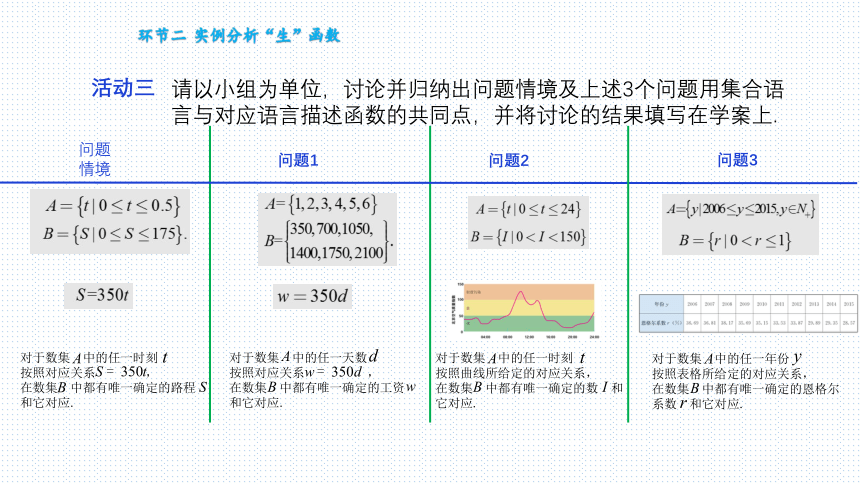
活动三
请以小组为单位,讨论并归纳出问题情境及上述3个问题用集合语言与对应语言描述函数的共同点,并将讨论的结果填写在学案上.
问题情境
问题1
问题2
问题3
对于数集 中的任一时刻
按照对应关系 ,
在数集 中都有唯一确定的路程 和它对应.
对于数集 中的任一天数
按照对应关系 ,
在数集 中都有唯一确定的工资 和它对应.
对于数集 中的任一时刻
按照曲线所给定的对应关系,
在数集 中都有唯一确定的数 和它对应.
对于数集 中的任一年份
按照表格所给定的对应关系,
在数集 中都有唯一确定的恩格尔系数 和它对应.
环节二 实例分析“生”函数
活动四
根据共同特征,以初中函数概念为基础,以小组为单位,讨论如何用集合语言与对应关系对函数概念重新下定义.
人民教育出版社出版的义务教育教科书八年级(下册)(教育部2013年审定)就是这么给出的:
一般地,在一个变化过程中,如果有两个变量 与 ,并且对于 的每一个确定的值, 都有唯一确定的值与其对应,那么我们就说 是自变量, 是 的函数.如果当 时 ,那么 叫做当自变量的值为 时的函数值.
环节二 实例分析“生”函数
环节二 实例分析“生”函数
初中抽象一次函数的过程
语言基础:A、B是两个非空数集
解析式
图 象
表 格
对于集合A中的任意一个数,按照某种确定的对应关系,
在集合B中都有唯一确定的数和它对应.
环节二 实例分析“生”函数
环节二 实例分析“生”函数
记为
环节二 实例分析“生”函数
伽利略(Galileo Galilei)
在17世纪早期,由于天文学和航海事业的发展,科学家以解释地球和天体运动作为研究课题,推动了函数概念的发展.1638年意大利科学家伽利略(Galileo Galilei)第一个提出了函数或称为变量关系的这一理念.
函数史话
莱布尼茨(Gottfried Leibniz)
“function(函数)”作为数学术语,是微积分奠基人之一、德国哲学家、数学家莱布尼茨(Gottfried Leibniz)在他1673年的手稿《切线的逆方法或函数方法》(Methodus tangentium inversa seu de functionibus)中首次使用.
莱布尼茨微分学手稿
函数史话
李善兰(1811-1882)
中文的“函数”一词是1859年中国清代数学家李善兰在翻译《代微积拾级》时,由“function”创译的.他给出的理由是“凡此变数中函彼变数者,则此为彼之函数”,即“函”为包含之意.
《代微积拾级》
函数史话
伯努利(Johann Bernoulli)
1718年,瑞士数学家伯努利(Johann Bernoulli)在关于等周问题的一篇论文中,把函数定义为:一个变量的函数是指由这个变量和某些常量以任何一种方式组成的量.这是历史上第一个正式发表的明确的函数定义.
伯努利和大数定律
函数史话
欧拉(Leonhard Euler)
1755年,瑞士数学家、物理学家欧拉(Leonhard Euler)在《微分学原理》的序言中进一步给出了函数的定义:
当变量以如下的方式依赖于另一些变量,即当后面这些变量变化时,前者也随之变化,则称前面的变量是后面变量的函数.
这就是人们通常称为函数定义的“变量说”.
函数史话
狄利克雷(Dirichlet)
在1837年,德国数学家狄利克雷再次拓展了函数的定义,他指出:“对于在某个区间上的每一个确定的x的值,y都有一个确定的值,那么y叫做x的函数”,从依赖到对应,人们认为函数概念、函数本质定义已经形成,这就是人们常说的经典函数定义.
函数史话
康托尔(Cantor)
在19世纪,随着德国数学康托尔创立集合论,美国数学家维布伦用“集合”与“对应”给出了近代函数定义,当然随着物理学等科学研究的需要,函数的概念还在进一步发展,真诚的希望,在座的同学们,也能像这些科学家一样,继续为函数概念的发展做出新的贡献.
函数史话
辨析1
集合A、B都是数集
环节三 剖析概念“辨”函数
A
1
2
3
4
5
B
1
2
3
4
5
A
1
2
3
4
5
B
1
2
3
4
5
A
1
2
3
4
5
B
1
2
3
4
5
A中元素的“任意性”
B中元素的唯一性
环节三 剖析概念“辨”函数
辨析2
环节三 剖析概念“辨”函数
定义域、对应关系、值域称为函数的三要素
用函数的定义重新认识一次函数、二次函数、反比例函数,指出它们的定义域、值域、对应关系.
环节四 经历实践“用”函数
应用一
试构建一个问题情境,使其中的变量关系可以用解析式
来描述.
环节四 经历实践“用”函数
应用二
感悟一
请从知识、方法、思想、应用等方面构建本节课的学习结构图.
环节五 总结反思“悟”函数
函数的概念
初中函数“变量说”
用集合语言对应关系定义函数
生活实例
再认识
抽象
应用
特殊到一般
科学发展
未来
三要素
知识增加
感悟二
本章章引言有这样一段话,说明函数概念及其反应的思想方法不仅是进一步学习数学的基础,也是学习其它学科的基础,更是解决问题的工具.
环节五 总结反思“悟”函数
学姐带我认识函数
环节五 总结反思“悟”函数
大家知道历史上很多的数学家也是哲学家,如罗素、毕达哥拉斯、莱布尼茨等等,可见数学和哲学关系密切.
2018年某大学自主招生考试题目就是:“谈谈数学与哲学的关系”.今天我们学习的函数概念的本源与哲学中的“运动”,函数三要素与哲学中的“联系”,函数表示与哲学中的“辩证法”等等.
环节六 感悟哲思“赏”函数
1.函数概念本源与哲学中的“运动”.
哲学讲“运动”,指的是宇宙间一切事物、现象的变化和过程.辩证唯物主义认为,运动是物质不可分离的根本属性,物质的任何形态都处于运动中,运动是物质存在最根本的形式.函数是研究自然科学中物质的变化现象的,并试图用量化的方式记录物质运动的存在形式。因此只有承认物质的运动、变化这一现实,函数才有存在的必要,从这个意义上讲,哲学中的运动和物质的辩证关系为函数概念提供了生存土壤.
2.函数三要素与哲学中的“联系”.
“联系”是一个普遍的哲学概念,指的是一切事物内部中的各部分,诸多要素之间的相互依存、相互影响和相互制约关系.辩证法认为联系是普遍存在的,世界就是一个普遍存在的有机整体.
函数定义中的定义域、对应关系、值域是函数的三要素,显然,它们相互依赖,缺一不可.
3.函数表示与哲学中的“辩证法”.
本节课给出的前四个问题,代表了函数在中学阶段的三种表示形式.
函数的多种表示形式是丰富多彩的社会实际的需求,体现了人们辩证的观察世界的一种立场、观念和方法.
解析式
图 象
表 格
解析式能够简明、全面的概括变量间的对应关系,将复杂的变化现象通过一个解析式清晰的表示出来,解析法体现了“现象与本质”的辩证关系,体现了“透过现象看本质”的方法论.
图象能直观形象地表示出函数值随着自变量的变化而变化的趋势,将抽象的函数关系用图形具体的表示出来.图象体现了“具体与抽象”的辩证关系.
表格不需要通过计算就可以直接得到与自变量对应的函数值,在生产实际中应用广泛.列表体现了“动与静”的辩证关系,动态的变量关系,采用静态的数据呈现,变化是绝对的,静止是相对的,动静结合,思想深刻.
人教A版《普通高中课程标准教科书 数学》必修第一册
函数概念起始课
2024年高中数学教学课件★★
环节一 创设情境“话”函数
根据短片,你能从中发现哪些函数关系?
环节一 创设情境“话”函数
(1)正方形的边长为,周长为
(2)
的函数.
正比例函数
VS
环节一 创设情境“话”函数
问题
情境
某“复兴号”高速列车加速到350km/h后保持匀速运行半小时.
(1)列车行进的路程S与运行时间t的关系是什么?
(2)你能用初中所学函数概念描述S与t的函数关系吗?
(3)有人说:“根据对应关系这趟列车加速到350km/h后, 运行1h就前进了350km.”你认为这个说法正确吗?
(4)如何用更精确的语言来描述S与t的函数关系呢?
(4)如何用更精确的语言来描述S与t的函数关系呢?
新教材在第一章《集合与常用逻辑用语》章引言曾讲到集合的作用:为了简洁、准确地表述数学对象及研究范围,我们需要使用集合的语言和工具.
环节一 创设情境“话”函数
环节一 创设情境“话”函数
(4)如何用更精确的语言来描述S与t的函数关系呢?
VS
和 是两个变量,而
且对于 的每一个确定值,
都有唯一确定值与之对应.
集合A
集合B
对应关系
变量t
变量S
对应
精确
完善
活动一
仿照问题情境,分别用初中函数概念、集合语言与对应关系研究下面三个问题实例,请以小组为单位讨论.
工人工资
空气质量指数
恩格尔系数
环节二 实例分析“生”函数
活动二
VS
集合-对应
“变量说”
对比发现,自我点评两种刻画函数的方法.
环节二 实例分析“生”函数
关于数学概念的生成,本书主编,人教社章建跃博士曾说:“数学的概念应该怎么获得?可以从大量同类事物的不同例证中找到它们的共同的关键特征. ”
环节二 实例分析“生”函数
活动三
请以小组为单位,讨论并归纳出问题情境及上述3个问题用集合语言与对应语言描述函数的共同点,并将讨论的结果填写在学案上.
问题情境
问题1
问题2
问题3
对于数集 中的任一时刻
按照对应关系 ,
在数集 中都有唯一确定的路程 和它对应.
对于数集 中的任一天数
按照对应关系 ,
在数集 中都有唯一确定的工资 和它对应.
对于数集 中的任一时刻
按照曲线所给定的对应关系,
在数集 中都有唯一确定的数 和它对应.
对于数集 中的任一年份
按照表格所给定的对应关系,
在数集 中都有唯一确定的恩格尔系数 和它对应.
环节二 实例分析“生”函数
活动四
根据共同特征,以初中函数概念为基础,以小组为单位,讨论如何用集合语言与对应关系对函数概念重新下定义.
人民教育出版社出版的义务教育教科书八年级(下册)(教育部2013年审定)就是这么给出的:
一般地,在一个变化过程中,如果有两个变量 与 ,并且对于 的每一个确定的值, 都有唯一确定的值与其对应,那么我们就说 是自变量, 是 的函数.如果当 时 ,那么 叫做当自变量的值为 时的函数值.
环节二 实例分析“生”函数
环节二 实例分析“生”函数
初中抽象一次函数的过程
语言基础:A、B是两个非空数集
解析式
图 象
表 格
对于集合A中的任意一个数,按照某种确定的对应关系,
在集合B中都有唯一确定的数和它对应.
环节二 实例分析“生”函数
环节二 实例分析“生”函数
记为
环节二 实例分析“生”函数
伽利略(Galileo Galilei)
在17世纪早期,由于天文学和航海事业的发展,科学家以解释地球和天体运动作为研究课题,推动了函数概念的发展.1638年意大利科学家伽利略(Galileo Galilei)第一个提出了函数或称为变量关系的这一理念.
函数史话
莱布尼茨(Gottfried Leibniz)
“function(函数)”作为数学术语,是微积分奠基人之一、德国哲学家、数学家莱布尼茨(Gottfried Leibniz)在他1673年的手稿《切线的逆方法或函数方法》(Methodus tangentium inversa seu de functionibus)中首次使用.
莱布尼茨微分学手稿
函数史话
李善兰(1811-1882)
中文的“函数”一词是1859年中国清代数学家李善兰在翻译《代微积拾级》时,由“function”创译的.他给出的理由是“凡此变数中函彼变数者,则此为彼之函数”,即“函”为包含之意.
《代微积拾级》
函数史话
伯努利(Johann Bernoulli)
1718年,瑞士数学家伯努利(Johann Bernoulli)在关于等周问题的一篇论文中,把函数定义为:一个变量的函数是指由这个变量和某些常量以任何一种方式组成的量.这是历史上第一个正式发表的明确的函数定义.
伯努利和大数定律
函数史话
欧拉(Leonhard Euler)
1755年,瑞士数学家、物理学家欧拉(Leonhard Euler)在《微分学原理》的序言中进一步给出了函数的定义:
当变量以如下的方式依赖于另一些变量,即当后面这些变量变化时,前者也随之变化,则称前面的变量是后面变量的函数.
这就是人们通常称为函数定义的“变量说”.
函数史话
狄利克雷(Dirichlet)
在1837年,德国数学家狄利克雷再次拓展了函数的定义,他指出:“对于在某个区间上的每一个确定的x的值,y都有一个确定的值,那么y叫做x的函数”,从依赖到对应,人们认为函数概念、函数本质定义已经形成,这就是人们常说的经典函数定义.
函数史话
康托尔(Cantor)
在19世纪,随着德国数学康托尔创立集合论,美国数学家维布伦用“集合”与“对应”给出了近代函数定义,当然随着物理学等科学研究的需要,函数的概念还在进一步发展,真诚的希望,在座的同学们,也能像这些科学家一样,继续为函数概念的发展做出新的贡献.
函数史话
辨析1
集合A、B都是数集
环节三 剖析概念“辨”函数
A
1
2
3
4
5
B
1
2
3
4
5
A
1
2
3
4
5
B
1
2
3
4
5
A
1
2
3
4
5
B
1
2
3
4
5
A中元素的“任意性”
B中元素的唯一性
环节三 剖析概念“辨”函数
辨析2
环节三 剖析概念“辨”函数
定义域、对应关系、值域称为函数的三要素
用函数的定义重新认识一次函数、二次函数、反比例函数,指出它们的定义域、值域、对应关系.
环节四 经历实践“用”函数
应用一
试构建一个问题情境,使其中的变量关系可以用解析式
来描述.
环节四 经历实践“用”函数
应用二
感悟一
请从知识、方法、思想、应用等方面构建本节课的学习结构图.
环节五 总结反思“悟”函数
函数的概念
初中函数“变量说”
用集合语言对应关系定义函数
生活实例
再认识
抽象
应用
特殊到一般
科学发展
未来
三要素
知识增加
感悟二
本章章引言有这样一段话,说明函数概念及其反应的思想方法不仅是进一步学习数学的基础,也是学习其它学科的基础,更是解决问题的工具.
环节五 总结反思“悟”函数
学姐带我认识函数
环节五 总结反思“悟”函数
大家知道历史上很多的数学家也是哲学家,如罗素、毕达哥拉斯、莱布尼茨等等,可见数学和哲学关系密切.
2018年某大学自主招生考试题目就是:“谈谈数学与哲学的关系”.今天我们学习的函数概念的本源与哲学中的“运动”,函数三要素与哲学中的“联系”,函数表示与哲学中的“辩证法”等等.
环节六 感悟哲思“赏”函数
1.函数概念本源与哲学中的“运动”.
哲学讲“运动”,指的是宇宙间一切事物、现象的变化和过程.辩证唯物主义认为,运动是物质不可分离的根本属性,物质的任何形态都处于运动中,运动是物质存在最根本的形式.函数是研究自然科学中物质的变化现象的,并试图用量化的方式记录物质运动的存在形式。因此只有承认物质的运动、变化这一现实,函数才有存在的必要,从这个意义上讲,哲学中的运动和物质的辩证关系为函数概念提供了生存土壤.
2.函数三要素与哲学中的“联系”.
“联系”是一个普遍的哲学概念,指的是一切事物内部中的各部分,诸多要素之间的相互依存、相互影响和相互制约关系.辩证法认为联系是普遍存在的,世界就是一个普遍存在的有机整体.
函数定义中的定义域、对应关系、值域是函数的三要素,显然,它们相互依赖,缺一不可.
3.函数表示与哲学中的“辩证法”.
本节课给出的前四个问题,代表了函数在中学阶段的三种表示形式.
函数的多种表示形式是丰富多彩的社会实际的需求,体现了人们辩证的观察世界的一种立场、观念和方法.
解析式
图 象
表 格
解析式能够简明、全面的概括变量间的对应关系,将复杂的变化现象通过一个解析式清晰的表示出来,解析法体现了“现象与本质”的辩证关系,体现了“透过现象看本质”的方法论.
图象能直观形象地表示出函数值随着自变量的变化而变化的趋势,将抽象的函数关系用图形具体的表示出来.图象体现了“具体与抽象”的辩证关系.
表格不需要通过计算就可以直接得到与自变量对应的函数值,在生产实际中应用广泛.列表体现了“动与静”的辩证关系,动态的变量关系,采用静态的数据呈现,变化是绝对的,静止是相对的,动静结合,思想深刻.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
