人教版数学七下 8.3实际问题与二元一次方程组(1)教案(表格式)
文档属性
| 名称 | 人教版数学七下 8.3实际问题与二元一次方程组(1)教案(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 55.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 00:00:00 | ||
图片预览

文档简介
8.3 实际问题与二元一次方程组
课题 第1课时 和差倍分问题 授课人
教 学 目 标 1.能够找出实际问题中的已知数和未知数,分析它们之间的数量关系,列出方程组. 2.学会比较估算与精确计算以及检验方程组的解是否符合题意并正确作答. 3.经历用方程组解决实际问题的过程,体会方程组是刻画现实世界中含有多个未知数的问题的有效数学模型. 4.通过方程模型建立二元一次方程组,从而解决实际问题. 5.培养学生分析、解决问题的能力,体会二元一次方程组的应用价值,感受数学文化.
教学 重点 确定解题策略,比较估算与精确计算.
教学 难点 以方程组为工具,分析、解决含有多个未知数的实际问题.
教学活动
教学 步骤 师生活动 设计意图
活动 一: 创设 情境 导入 新课 【课堂引入】 前面我们结合实际问题,讨论了用方程组表示问题中的条件以及如何解方程组.本节课我们继续探究如何用方程组解决实际问题. 开门见山,直接提出本节课学习内容,突出数学与现实的联系.
活动 二: 探究 与 应用 【探究】 养牛场原有30头大牛和15头小牛,一天约用饲料675 kg;一周后又购进12头大牛和5头小牛,这时一天约用饲料940 kg.饲养员李大叔估计每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7~8 kg.请你通过计算检验李大叔的估计是否正确. 请同学们讨论: (1)问题中有几个未知量 (2)你准备设哪几个未知数 (3)你能在问题中把表示相等关系的语句找出来,并用等式进行表示吗 (4)你能依据上面的相等关系列出方程或方程组吗 问题1:如何理解“通过计算检验李大叔的估计是否正确”这句话 问题2:题目中哪些是已知量,哪些是未知量 有几个相等关系 找出题中的未知量,设出未知数. 设每头大牛1天约用饲料x kg,每头小牛1天约用饲料y kg. 确定题目当中的两个相等关系,根据这两个相等关系利用所设未知数列出两个等式. 问题3:列出二元一次方程组解决这个问题: 问题4:请你解这个方程组,并交流一下你是如何解这个方程组的 解:设每头大牛1天约用饲料x kg,每头小牛1天约用饲料y kg, 则解得 问题5:饲养员李大叔的估计正确吗 每头大牛1天约需饲料20 kg,每头小牛1天约需饲料5 kg,所以饲养员李大叔对大牛的食量估计准确,对小牛的食量估计偏高. 总结解应用题的方法,思考下列问题: (1)在列方程组之前我们先做了哪些工作 (2)列方程组解决实际问题的一般步骤是什么 指导学生分析题目,确定未知数及相等关系.
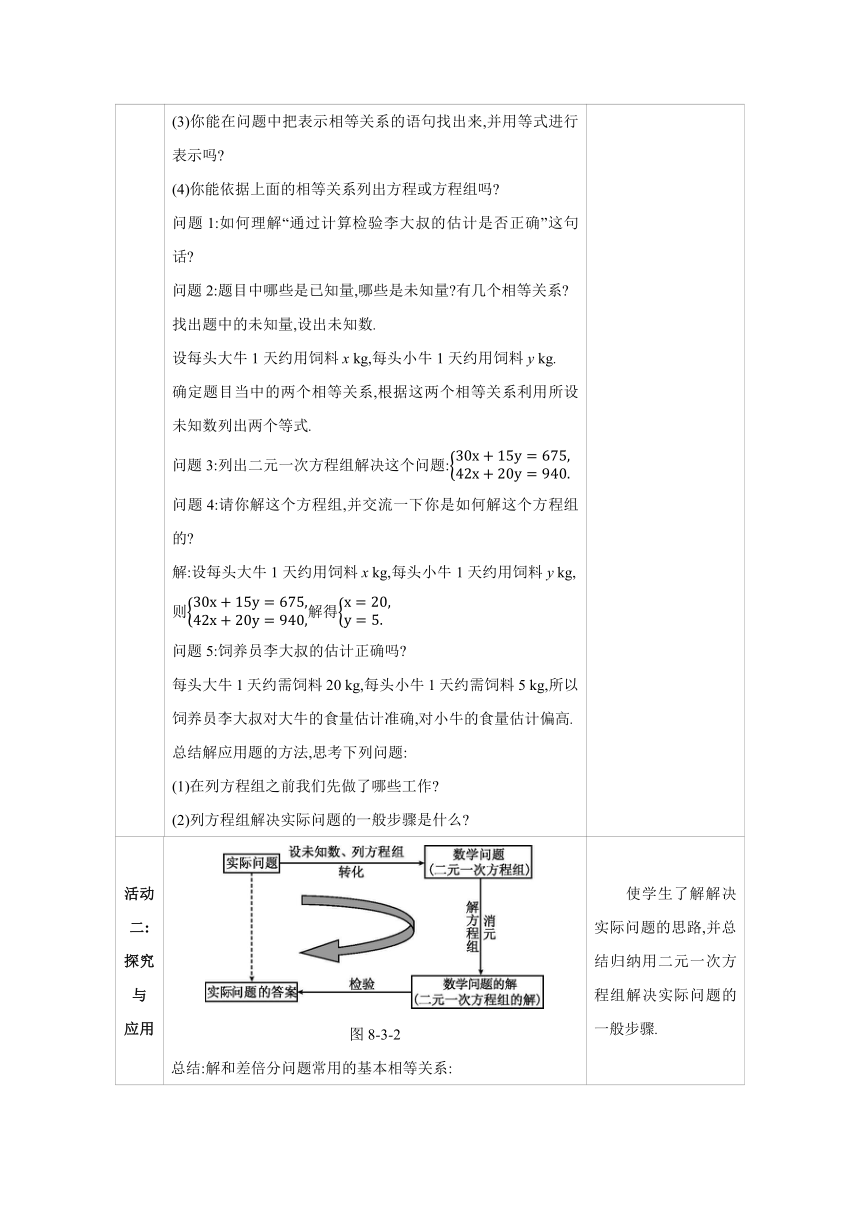
活动 二: 探究 与 应用 图8-3-2 总结:解和差倍分问题常用的基本相等关系: 较大量=较小量+多余量; 总量=一份的量×倍数; 各分量相加=总量. 使学生了解解决实际问题的思路,并总结归纳用二元一次方程组解决实际问题的一般步骤.
【应用举例】 例1 某校师生积极为地震灾区捐款,在得知灾区急需帐篷后,立即到当地的一家帐篷厂采购,帐篷有两种规格:可供3人居住的小帐篷,价格为每顶160元;可供10人居住的大帐篷,价格为每顶400元.学校花去捐款96000元,正好可供2300人临时居住.该校采购了多少顶3人小帐篷,多少顶10人大帐篷 变式 学校总务处与教务处各领了同样数量的信封和信笺,总务处每发出一封信只用一张信笺,教务处每发出一封信都用3张信笺,结果,总务处用掉了所有的信封,但余下50张信笺,而教务处用掉了所有的信笺,但余下50个信封,则两处所领的信笺和信封各是多少 【拓展提升】 例2 已进入汛期,七年级(一)班的同学们到水库去调查了解汛情.水库一共有10个泄洪闸,现在水库水位已超过安全线,上游的河水仍以一个不变的速度流入水库.同学们经过一天的观察和测量,做了如下记录:上午打开一个泄洪闸,在2小时内水位继续上涨了0.06米;下午再打开2个泄洪闸后,4小时内水位下降了0.1米.目前水位仍超过安全线1.2米. (1)如果打开了5个泄洪闸,还需几小时水位降到安全线 (2)如果防汛指挥部要求在6小时内使水位降到安全线,应该打开几个泄洪闸 通过构造二元一次方程组解决实际问题. 综合考查学生利用知识解决实际问题的能力.
活动 三: 课堂 总结 反思 【当堂训练】 1.一张试卷有25道题,做对一题得4分,做错一题扣1分,小明做了全部试题得70分,则他做对的题数是 ( ) A.16 B.17 C.18 D.19 2.现在父亲的年龄是儿子的年龄的3倍,7年前父亲的年龄是儿子的年龄的5倍,父亲、儿子现在的年龄分别是 ( ) A.42岁,14岁 B.48岁,16岁 C.36岁,12岁 D.39岁,13岁 3.用一根绳子环绕一个圆柱形油桶,若环绕油桶3周,则绳子还多4尺;若环绕油桶4周,则绳子又少了3尺,这根绳子有多长 环绕油桶一周需要几尺 【课后作业】 课本第101页习题8.3第1,2,3题. 通过练习进一步巩固列方程解应用题.
【板书设计】 第1课时 和差倍分问题 列二元一次方程组解应用题的一般步骤: 设 用两个字母表示问题中的两个未知数 列 列出方程组 解 解方程组,求出未知数的值 验 检验求得的值是否正确和符合实际意义 答 写出答案 和差倍分应用题中常见的相等关系: 较大量=较小量+多余量 总量=一份的量×倍数 各分量相加=总量 提纲挈领,重点突出.
课题 第1课时 和差倍分问题 授课人
教 学 目 标 1.能够找出实际问题中的已知数和未知数,分析它们之间的数量关系,列出方程组. 2.学会比较估算与精确计算以及检验方程组的解是否符合题意并正确作答. 3.经历用方程组解决实际问题的过程,体会方程组是刻画现实世界中含有多个未知数的问题的有效数学模型. 4.通过方程模型建立二元一次方程组,从而解决实际问题. 5.培养学生分析、解决问题的能力,体会二元一次方程组的应用价值,感受数学文化.
教学 重点 确定解题策略,比较估算与精确计算.
教学 难点 以方程组为工具,分析、解决含有多个未知数的实际问题.
教学活动
教学 步骤 师生活动 设计意图
活动 一: 创设 情境 导入 新课 【课堂引入】 前面我们结合实际问题,讨论了用方程组表示问题中的条件以及如何解方程组.本节课我们继续探究如何用方程组解决实际问题. 开门见山,直接提出本节课学习内容,突出数学与现实的联系.
活动 二: 探究 与 应用 【探究】 养牛场原有30头大牛和15头小牛,一天约用饲料675 kg;一周后又购进12头大牛和5头小牛,这时一天约用饲料940 kg.饲养员李大叔估计每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7~8 kg.请你通过计算检验李大叔的估计是否正确. 请同学们讨论: (1)问题中有几个未知量 (2)你准备设哪几个未知数 (3)你能在问题中把表示相等关系的语句找出来,并用等式进行表示吗 (4)你能依据上面的相等关系列出方程或方程组吗 问题1:如何理解“通过计算检验李大叔的估计是否正确”这句话 问题2:题目中哪些是已知量,哪些是未知量 有几个相等关系 找出题中的未知量,设出未知数. 设每头大牛1天约用饲料x kg,每头小牛1天约用饲料y kg. 确定题目当中的两个相等关系,根据这两个相等关系利用所设未知数列出两个等式. 问题3:列出二元一次方程组解决这个问题: 问题4:请你解这个方程组,并交流一下你是如何解这个方程组的 解:设每头大牛1天约用饲料x kg,每头小牛1天约用饲料y kg, 则解得 问题5:饲养员李大叔的估计正确吗 每头大牛1天约需饲料20 kg,每头小牛1天约需饲料5 kg,所以饲养员李大叔对大牛的食量估计准确,对小牛的食量估计偏高. 总结解应用题的方法,思考下列问题: (1)在列方程组之前我们先做了哪些工作 (2)列方程组解决实际问题的一般步骤是什么 指导学生分析题目,确定未知数及相等关系.
活动 二: 探究 与 应用 图8-3-2 总结:解和差倍分问题常用的基本相等关系: 较大量=较小量+多余量; 总量=一份的量×倍数; 各分量相加=总量. 使学生了解解决实际问题的思路,并总结归纳用二元一次方程组解决实际问题的一般步骤.
【应用举例】 例1 某校师生积极为地震灾区捐款,在得知灾区急需帐篷后,立即到当地的一家帐篷厂采购,帐篷有两种规格:可供3人居住的小帐篷,价格为每顶160元;可供10人居住的大帐篷,价格为每顶400元.学校花去捐款96000元,正好可供2300人临时居住.该校采购了多少顶3人小帐篷,多少顶10人大帐篷 变式 学校总务处与教务处各领了同样数量的信封和信笺,总务处每发出一封信只用一张信笺,教务处每发出一封信都用3张信笺,结果,总务处用掉了所有的信封,但余下50张信笺,而教务处用掉了所有的信笺,但余下50个信封,则两处所领的信笺和信封各是多少 【拓展提升】 例2 已进入汛期,七年级(一)班的同学们到水库去调查了解汛情.水库一共有10个泄洪闸,现在水库水位已超过安全线,上游的河水仍以一个不变的速度流入水库.同学们经过一天的观察和测量,做了如下记录:上午打开一个泄洪闸,在2小时内水位继续上涨了0.06米;下午再打开2个泄洪闸后,4小时内水位下降了0.1米.目前水位仍超过安全线1.2米. (1)如果打开了5个泄洪闸,还需几小时水位降到安全线 (2)如果防汛指挥部要求在6小时内使水位降到安全线,应该打开几个泄洪闸 通过构造二元一次方程组解决实际问题. 综合考查学生利用知识解决实际问题的能力.
活动 三: 课堂 总结 反思 【当堂训练】 1.一张试卷有25道题,做对一题得4分,做错一题扣1分,小明做了全部试题得70分,则他做对的题数是 ( ) A.16 B.17 C.18 D.19 2.现在父亲的年龄是儿子的年龄的3倍,7年前父亲的年龄是儿子的年龄的5倍,父亲、儿子现在的年龄分别是 ( ) A.42岁,14岁 B.48岁,16岁 C.36岁,12岁 D.39岁,13岁 3.用一根绳子环绕一个圆柱形油桶,若环绕油桶3周,则绳子还多4尺;若环绕油桶4周,则绳子又少了3尺,这根绳子有多长 环绕油桶一周需要几尺 【课后作业】 课本第101页习题8.3第1,2,3题. 通过练习进一步巩固列方程解应用题.
【板书设计】 第1课时 和差倍分问题 列二元一次方程组解应用题的一般步骤: 设 用两个字母表示问题中的两个未知数 列 列出方程组 解 解方程组,求出未知数的值 验 检验求得的值是否正确和符合实际意义 答 写出答案 和差倍分应用题中常见的相等关系: 较大量=较小量+多余量 总量=一份的量×倍数 各分量相加=总量 提纲挈领,重点突出.
