6.2 排列与组合 课件(共23张PPT)
文档属性
| 名称 | 6.2 排列与组合 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 506.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
排列与组合(1)
【排列】①从n个不同元素中取出m(m≤n)个元素,
②按一定的顺序排成一列.
【关键点】1.互异性(被选、所选元素互不相同)
2.有序性(所选元素有先后位置等顺序之分)
【排列数】所有排列方法的总数
(其中n,m∈N*,且m ≤n)
复习回顾
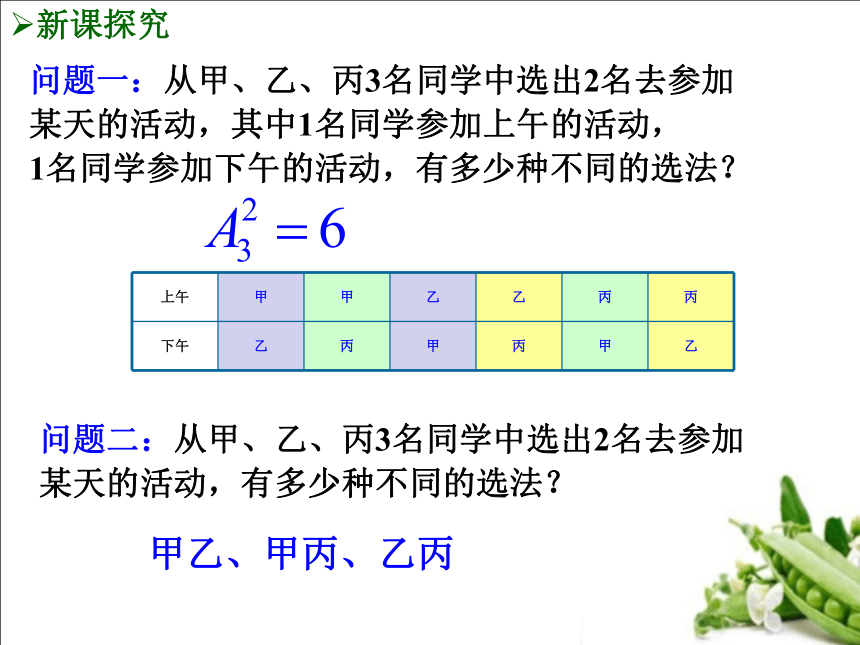
问题一:从甲、乙、丙3名同学中选出2名去参加
某天的活动,其中1名同学参加上午的活动,
1名同学参加下午的活动,有多少种不同的选法?
问题二:从甲、乙、丙3名同学中选出2名去参加
某天的活动,有多少种不同的选法?
甲乙、甲丙、乙丙
上午 甲 甲 乙 乙 丙 丙
下午 乙 丙 甲 丙 甲 乙
新课探究
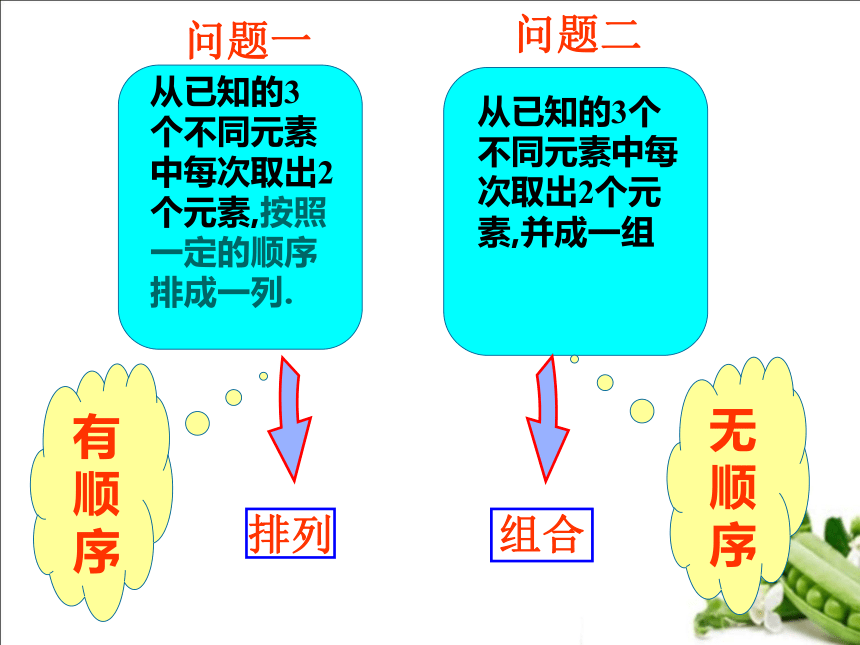
从已知的3个不同元素中每次取出2个元素,并成一组
问题二
从已知的3 个不同元素中每次取出2个元素,按照一定的顺序排成一列.
问题一
排列
组合
有
顺
序
无
顺
序
1.组合定义: 一般地,从n个不同元素中取出m(m≤n)个元素合成一组,叫做从n个不同元素中取出m个元素的一个组合.
排列定义: 一般地,从n个不同元素中取出m (m≤n) 个元素,按照一定的顺序排成一列,叫做从 n 个不同元素中取出 m 个元素的一个排列.
共同点: 都要“从n个不同元素中任取m个元素”
不同点: 排列与元素的顺序有关,
而组合则与元素的顺序无关.
概念讲解
组合是选择的结果,排列
是选择后再排序的结果.
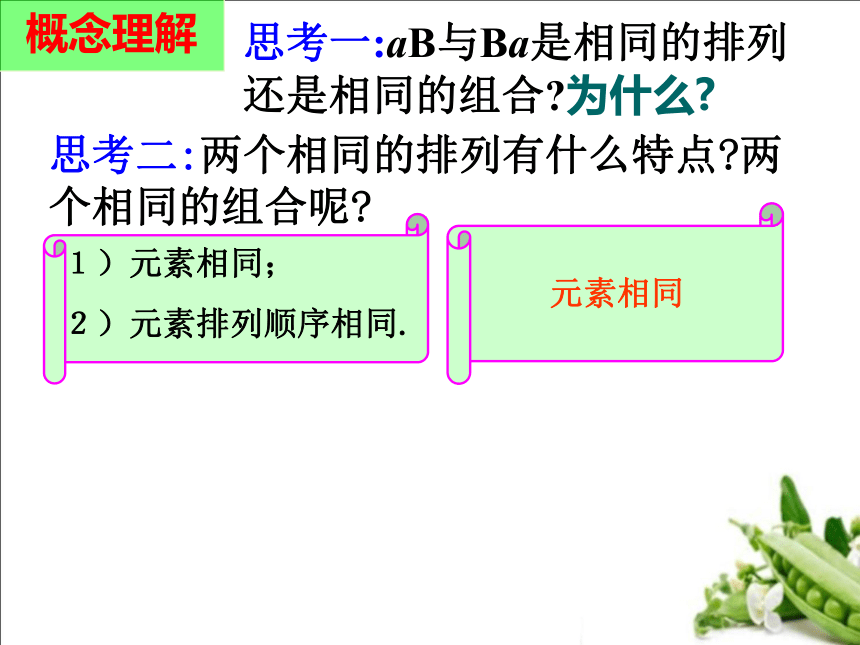
思考一:aB与Ba是相同的排列 还是相同的组合 为什么
思考二:两个相同的排列有什么特点 两个相同的组合呢
1)元素相同;
2)元素排列顺序相同.
元素相同
概念理解
1、判断下列问题是组合问题还是排列问题
(1)从4个大小相同、颜色不同的小球中取出2个,共有多少种取法
组合问题
(4)10人聚会,见面后每两人之间要握手相互问候,共需握手多少次
组合问题
(5) 10位同学每两人之间相互发手机短信一条问候对方,求共发了多少条短信?
排列问题
(2)从4个大小相同、颜色不同的小球中取出2个放入两个不同的盒子中,共有多少种取法
排列问题
(3)从4个大小相同、颜色相同的小球中取出2个,共有多少种取法
不是排列也不是组合问题
组合:只选不排
排列:选后再排
课堂练习
2.从 a , b , c三个不同的元素中取出两个元素的所有组合分别是:
3.已知四个不同元素a , b , c , d ,写出每次取出两个元素的所有组合:
4.从四个不同元素a,b,c,d中取出三个元素的所有
组合:
课堂练习
从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号 表示.
2、组合数:
基础知识讲解
2.写出从a、b、c三个元素中取出两个元素的所有组合;
3.写出从a、b、c、d四个元素中取出两个元素的所有组合;
4.写出从a、b、c、d四个元素中取出三个元素的所有组合.
ab、ac、bc
ab、ac、ad、bc、bd、cd
abc、abd、acd、bcd
从a,b,c,d 四个元素中任取三个元素的所有组合。
abc , abd , acd , bcd .
从a,b,c,d 四个元素中任取三个元素的所有排列。
c d
b d
b c
c d
a c
a d
b d
a d
a b
b c
a c
a b
b c d
a c d
a b d
a b c
b
a
c
d
循序渐进,探求新知:
abc bac cab dab
abd bad cad dac
acb bca cba dba
acd bcd cbd dbc
adb bda cda dca
adc bdc cdb dcb
所有的排列为:
排列数与组合数:
探究
所有组合
所有排列
abc
abd
acd
bcd
abc bac cab
acb bca cba
abd bad dab
adb bda dba
acd cad dac
adc cda dca
bcd cbd dbc
bdc cdb dcb
a
b
c
d
取出3个元素
你发现排列与组合的联系了吗?
归纳总结
归纳总结
组合数公式:
乘积形式
阶乘形式
小试牛刀
【例2】一位教练的足球队共有17名初级学员,他们中以前没有一人参加过比赛,按照足球比赛规则,比赛时一个足球队的上场队员是11人,问:
(1)这些学员可以形成多少种上场方案?
解:
例题分析
【例2】一位教练的足球队共有17名初级学员,他们中以前没有一人参加过比赛,按照足球比赛规则,比赛时一个足球队的上场队员是11人,问:
(2)如果在选出11名上场队员时,还要确定其中的
守门员,那么教练员有多少种方式做这件事情?
解:
例题分析
1、本节课你学到了哪些知识?
2、本节课用到了哪些数学方法?
组合
组合的概念
组合是选择的
结果,排列是
选择后再排序
的结果
联系
排列
类比推理,
归纳推理。
课堂小结
组合数的概念
组合数的公式
作业:
1、课本P25:1,2,3,4
2、探究:
组合数的两个性质
谢谢大家!
最后以一首小诗结束本节课的学习:
排列组合两兄弟,
有无顺序辨清晰;
先选后排有条理,
幸运计数就是你。
排列与组合(1)
【排列】①从n个不同元素中取出m(m≤n)个元素,
②按一定的顺序排成一列.
【关键点】1.互异性(被选、所选元素互不相同)
2.有序性(所选元素有先后位置等顺序之分)
【排列数】所有排列方法的总数
(其中n,m∈N*,且m ≤n)
复习回顾
问题一:从甲、乙、丙3名同学中选出2名去参加
某天的活动,其中1名同学参加上午的活动,
1名同学参加下午的活动,有多少种不同的选法?
问题二:从甲、乙、丙3名同学中选出2名去参加
某天的活动,有多少种不同的选法?
甲乙、甲丙、乙丙
上午 甲 甲 乙 乙 丙 丙
下午 乙 丙 甲 丙 甲 乙
新课探究
从已知的3个不同元素中每次取出2个元素,并成一组
问题二
从已知的3 个不同元素中每次取出2个元素,按照一定的顺序排成一列.
问题一
排列
组合
有
顺
序
无
顺
序
1.组合定义: 一般地,从n个不同元素中取出m(m≤n)个元素合成一组,叫做从n个不同元素中取出m个元素的一个组合.
排列定义: 一般地,从n个不同元素中取出m (m≤n) 个元素,按照一定的顺序排成一列,叫做从 n 个不同元素中取出 m 个元素的一个排列.
共同点: 都要“从n个不同元素中任取m个元素”
不同点: 排列与元素的顺序有关,
而组合则与元素的顺序无关.
概念讲解
组合是选择的结果,排列
是选择后再排序的结果.
思考一:aB与Ba是相同的排列 还是相同的组合 为什么
思考二:两个相同的排列有什么特点 两个相同的组合呢
1)元素相同;
2)元素排列顺序相同.
元素相同
概念理解
1、判断下列问题是组合问题还是排列问题
(1)从4个大小相同、颜色不同的小球中取出2个,共有多少种取法
组合问题
(4)10人聚会,见面后每两人之间要握手相互问候,共需握手多少次
组合问题
(5) 10位同学每两人之间相互发手机短信一条问候对方,求共发了多少条短信?
排列问题
(2)从4个大小相同、颜色不同的小球中取出2个放入两个不同的盒子中,共有多少种取法
排列问题
(3)从4个大小相同、颜色相同的小球中取出2个,共有多少种取法
不是排列也不是组合问题
组合:只选不排
排列:选后再排
课堂练习
2.从 a , b , c三个不同的元素中取出两个元素的所有组合分别是:
3.已知四个不同元素a , b , c , d ,写出每次取出两个元素的所有组合:
4.从四个不同元素a,b,c,d中取出三个元素的所有
组合:
课堂练习
从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号 表示.
2、组合数:
基础知识讲解
2.写出从a、b、c三个元素中取出两个元素的所有组合;
3.写出从a、b、c、d四个元素中取出两个元素的所有组合;
4.写出从a、b、c、d四个元素中取出三个元素的所有组合.
ab、ac、bc
ab、ac、ad、bc、bd、cd
abc、abd、acd、bcd
从a,b,c,d 四个元素中任取三个元素的所有组合。
abc , abd , acd , bcd .
从a,b,c,d 四个元素中任取三个元素的所有排列。
c d
b d
b c
c d
a c
a d
b d
a d
a b
b c
a c
a b
b c d
a c d
a b d
a b c
b
a
c
d
循序渐进,探求新知:
abc bac cab dab
abd bad cad dac
acb bca cba dba
acd bcd cbd dbc
adb bda cda dca
adc bdc cdb dcb
所有的排列为:
排列数与组合数:
探究
所有组合
所有排列
abc
abd
acd
bcd
abc bac cab
acb bca cba
abd bad dab
adb bda dba
acd cad dac
adc cda dca
bcd cbd dbc
bdc cdb dcb
a
b
c
d
取出3个元素
你发现排列与组合的联系了吗?
归纳总结
归纳总结
组合数公式:
乘积形式
阶乘形式
小试牛刀
【例2】一位教练的足球队共有17名初级学员,他们中以前没有一人参加过比赛,按照足球比赛规则,比赛时一个足球队的上场队员是11人,问:
(1)这些学员可以形成多少种上场方案?
解:
例题分析
【例2】一位教练的足球队共有17名初级学员,他们中以前没有一人参加过比赛,按照足球比赛规则,比赛时一个足球队的上场队员是11人,问:
(2)如果在选出11名上场队员时,还要确定其中的
守门员,那么教练员有多少种方式做这件事情?
解:
例题分析
1、本节课你学到了哪些知识?
2、本节课用到了哪些数学方法?
组合
组合的概念
组合是选择的
结果,排列是
选择后再排序
的结果
联系
排列
类比推理,
归纳推理。
课堂小结
组合数的概念
组合数的公式
作业:
1、课本P25:1,2,3,4
2、探究:
组合数的两个性质
谢谢大家!
最后以一首小诗结束本节课的学习:
排列组合两兄弟,
有无顺序辨清晰;
先选后排有条理,
幸运计数就是你。
