2024年四川省成都市中考数学预测题(一)(无答案)
文档属性
| 名称 | 2024年四川省成都市中考数学预测题(一)(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 662.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 14:56:43 | ||
图片预览


文档简介
姓名__________准考证号__________
2024年成都市高中阶段教育学校统一招生,
暨初中学业水平考试
中考预测卷数学(一)
注意事项:
1.全卷分A卷和B卷,A卷满分100分,B卷满分50分;考试时间120分钟.
2.在作答前,考生务必将自己的姓名、准考证号涂写在试卷和答题卡规定的地方.考试结束,监考人员将试卷和答题卡一并收回.
3.选择题部分必须使用2B铅笔填涂;非选择题部分必须使用0.5毫米黑色签字笔书写,字体工整、笔迹清楚.
4.请按照题号在答题卡上各题目对应的答题区域内作答,超出答题区城书写的答案无效;在草稿纸、试卷上答题均无效.
5.保持答题卡清洁,不得有折叠、污染、破损等.
A卷(共100分)
第I卷(选择题,共32分)
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求,把序号涂在答题卡上)
1.在,,0,四个数中,最小的数是( )
A. B. C.0 D.
2.2023年上半年我国新能源汽车取得显著成绩,新能源汽车使用环境持续优化,截至6月底,全国累计建成各类充电桩超过660万台.将数据“660万”用科学记数法表示为( )
A. B. C. D.
3.下列计算正确的是( )
A. B.
C. D.
4.2023年7月28日至8月8日,第31届世界大学生夏季运动会在四川省成都市举行,为此,成都市共建成49个场馆,其中新建场馆13处,改造场馆36处.大运村设在成都大学,依托现有校区和建设发展规划,新建生活服务中心、医疗中心、国际教育交流中心、实训楼等单体建筑22栋.数据49,13,36,22的中位数为( )
A.13 B.24.5 C.29 D.36
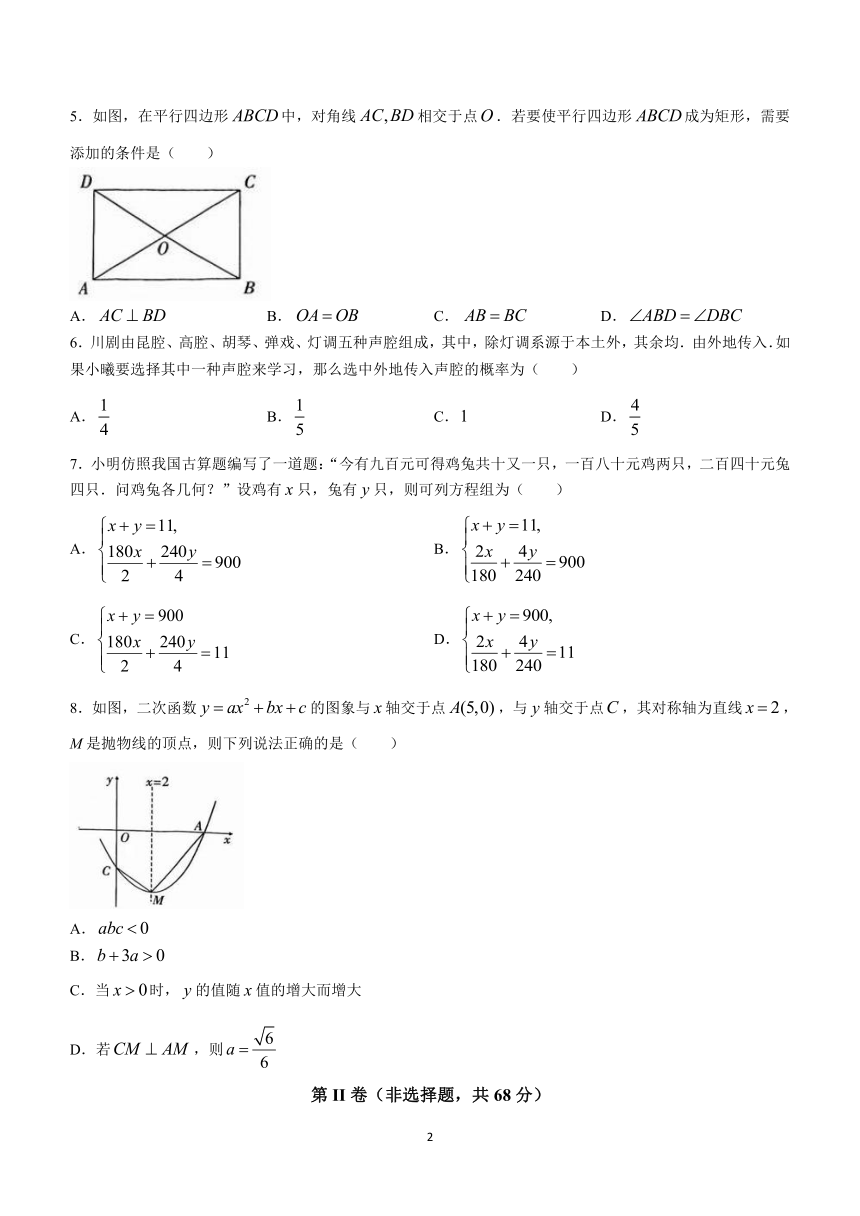
5.如图,在平行四边形中,对角线相交于点.若要使平行四边形成为矩形,需要添加的条件是( )
A. B. C. D.
6.川剧由昆腔、高腔、胡琴、弹戏、灯调五种声腔组成,其中,除灯调系源于本土外,其余均.由外地传入.如果小曦要选择其中一种声腔来学习,那么选中外地传入声腔的概率为( )
A. B. C. D.
7.小明仿照我国古算题编写了一道题:“今有九百元可得鸡兔共十又一只,一百八十元鸡两只,二百四十元兔四只.问鸡兔各几何?”设鸡有只,兔有只,则可列方程组为( )
A. B.
C. D.
8.如图,二次函数的图象与轴交于点,与轴交于点,其对称轴为直线,M是抛物线的顶点,则下列说法正确的是( )
A.
B.
C.当时,的值随值的增大而增大
D.若,则
第II卷(非选择题,共68分)
二、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)
9.因式分解:__________.
10.已知反比例函数图象上的两点,,且,则的取值范围是__________.
11.如图,,,,则__________.
12.在平面直角坐标系中,点关于轴对称的点的坐标为__________.
13.如图,为锐角三角形,点在边上,.分别以点A,C为圆心、大于的长为半径作弧,两弧相交于点E,F,作直线交于点.若,的面积为8,则的面积为__________.
三、解答题(本大题共5个小题,共48分,解答过程写在答题卡上)
14.(本小题满分12分,每题6分)
(1)计算:; (2)解不等式组:
15.(本小题满分8分)
成都市某中学为2024年“尤伯杯”预热,组织全校学生参加了“尤伯杯羽毛球比赛”知识竞赛,为了解全校学生竞赛成绩(单位:分)的情况,随机抽取了一部分学生的成绩,分成四组:A.70分以下(不包括70);B.;C.;D.,并绘制了如下两幅不完整的统计图.
根据上述信息,解答下列问题.
(1)被抽取的学生成绩在C组的有__________人,请补全条形统计图;
(2)被抽取的学生成绩在B组的对应扇形圆心角的度数是有__________,若该中学全校共有3600人,则成绩在A组的大约有__________人;
(3)现从D组前四名(2名男生和2名女生)中任选2名代表发表感言,请用列表或画树状图的方法,求选中1名男生和1名女生的概率.
16.(本小题满分8分)
屏风是一种古老的家具,它作为一种灵活的空间元素、装饰元素和设计元素,具有实用和艺术欣赏两方面的功能,能通过自身形状、色彩、质地、图案等特质融于丰富多元的现代空间环境,传达着新中式的意味,演绎出中国传统文化韵味,因此至今仍然被广泛地运用.小曦在房间墙角摆放了一架双面屏风,俯视图如图所示,两面屏风与墙角围成了一个独立空间用来堆放杂物,经测量,,请算出这个独立空间的面积.(结果精确到.参考数据:,)
17.(本小题满分10分)
如图,在中,,与相切于点,点为上一点,平分,和分别与相交于点,于点.
(1)求证:是的切线;
(2)若,的半径为,求的长.
18.(本小题满分10分)
如图,在平面直角坐标系中,一次函数的图象与坐标轴交于点A,B,与反比例函数的图象交于点,D是反比例函数图象上的一个动点,过点向轴作垂线与一次函数图象交于点,其中点的坐标为.
(1)求反比例函数的表达式;
(2)连接,当的面积等于面积的2倍时,求点的坐标;
(3)若P是x轴上的一个动点,连接,当与相似时,求点D的纵坐标.
B卷(共50分)
一、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)
19.已知非零实数a,b满足,则__________.
20.已知一元二次方程的一个根为,则的值为__________.
21.“不倒翁”玩具的主视图如图所示,分别与不倒翁底部所在的相切于点A,B,若的半径为,,则劣弧的长为__________.(结果保留)
22.一个直角三角形的边长都是整数,则称这种直角三角形为“完美勾股三角形”,k为其面积和周长的比值.当时,满足条件的“完美勾股三角形”的周长为__________;当时,若存在“完美勾股三角形”,则__________.
23.如图,在正方形中,是的中点,是边上一动点,将沿翻折得,连接,在左侧有一点,使得为等腰直角三角形,且,连接.若正方形的边长为6,则的最小值为__________.
二、解答题(本大题共3个小题,共30分,解答过程写在答题卡上)
24.(本小题满分8分)
2024年世界园艺博览会将在成都举行,某社区决定采购甲、乙两种盆栽美化环境,若购买20盆甲种盆栽和10盆乙种盆栽,则需要130元;若购买30盆甲种盆栽和20盆乙种盆栽,则需要220元.
(1)甲、乙两种盆栽的单价各是多少元?
(2)若该社区联合附近社区购买甲、乙两种盆栽共1000盆,设购买m盆()乙种盆栽,总费用为W元,请你帮社区设计一种购买方案,使总花费最少,并求出最少费用.
25.(本小题满分10分)
如图,在平面直角坐标系中,已知一抛物线经过原点,与轴交于另一点,顶点坐标为,过点的直线与抛物线交于点B,C,且点在点的左侧.
(1)求抛物线的函数表达式;
(2)连接,当的面积与的面积之比为1:2时,求直线的函数表达式;
(3)若有直线,点到直线的距离为,点到直线的距离为,求证:.
26.(本小题满分12分)
如图,已知为等边三角形,D,E分别是边上一点,与相交于点,点是射线上一点,且,与相交于点.
(1)求的度数;
(2)求证:是的中点;
(3)若,,求的边长.
2024年成都市高中阶段教育学校统一招生,
暨初中学业水平考试
中考预测卷数学(一)
注意事项:
1.全卷分A卷和B卷,A卷满分100分,B卷满分50分;考试时间120分钟.
2.在作答前,考生务必将自己的姓名、准考证号涂写在试卷和答题卡规定的地方.考试结束,监考人员将试卷和答题卡一并收回.
3.选择题部分必须使用2B铅笔填涂;非选择题部分必须使用0.5毫米黑色签字笔书写,字体工整、笔迹清楚.
4.请按照题号在答题卡上各题目对应的答题区域内作答,超出答题区城书写的答案无效;在草稿纸、试卷上答题均无效.
5.保持答题卡清洁,不得有折叠、污染、破损等.
A卷(共100分)
第I卷(选择题,共32分)
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求,把序号涂在答题卡上)
1.在,,0,四个数中,最小的数是( )
A. B. C.0 D.
2.2023年上半年我国新能源汽车取得显著成绩,新能源汽车使用环境持续优化,截至6月底,全国累计建成各类充电桩超过660万台.将数据“660万”用科学记数法表示为( )
A. B. C. D.
3.下列计算正确的是( )
A. B.
C. D.
4.2023年7月28日至8月8日,第31届世界大学生夏季运动会在四川省成都市举行,为此,成都市共建成49个场馆,其中新建场馆13处,改造场馆36处.大运村设在成都大学,依托现有校区和建设发展规划,新建生活服务中心、医疗中心、国际教育交流中心、实训楼等单体建筑22栋.数据49,13,36,22的中位数为( )
A.13 B.24.5 C.29 D.36
5.如图,在平行四边形中,对角线相交于点.若要使平行四边形成为矩形,需要添加的条件是( )
A. B. C. D.
6.川剧由昆腔、高腔、胡琴、弹戏、灯调五种声腔组成,其中,除灯调系源于本土外,其余均.由外地传入.如果小曦要选择其中一种声腔来学习,那么选中外地传入声腔的概率为( )
A. B. C. D.
7.小明仿照我国古算题编写了一道题:“今有九百元可得鸡兔共十又一只,一百八十元鸡两只,二百四十元兔四只.问鸡兔各几何?”设鸡有只,兔有只,则可列方程组为( )
A. B.
C. D.
8.如图,二次函数的图象与轴交于点,与轴交于点,其对称轴为直线,M是抛物线的顶点,则下列说法正确的是( )
A.
B.
C.当时,的值随值的增大而增大
D.若,则
第II卷(非选择题,共68分)
二、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)
9.因式分解:__________.
10.已知反比例函数图象上的两点,,且,则的取值范围是__________.
11.如图,,,,则__________.
12.在平面直角坐标系中,点关于轴对称的点的坐标为__________.
13.如图,为锐角三角形,点在边上,.分别以点A,C为圆心、大于的长为半径作弧,两弧相交于点E,F,作直线交于点.若,的面积为8,则的面积为__________.
三、解答题(本大题共5个小题,共48分,解答过程写在答题卡上)
14.(本小题满分12分,每题6分)
(1)计算:; (2)解不等式组:
15.(本小题满分8分)
成都市某中学为2024年“尤伯杯”预热,组织全校学生参加了“尤伯杯羽毛球比赛”知识竞赛,为了解全校学生竞赛成绩(单位:分)的情况,随机抽取了一部分学生的成绩,分成四组:A.70分以下(不包括70);B.;C.;D.,并绘制了如下两幅不完整的统计图.
根据上述信息,解答下列问题.
(1)被抽取的学生成绩在C组的有__________人,请补全条形统计图;
(2)被抽取的学生成绩在B组的对应扇形圆心角的度数是有__________,若该中学全校共有3600人,则成绩在A组的大约有__________人;
(3)现从D组前四名(2名男生和2名女生)中任选2名代表发表感言,请用列表或画树状图的方法,求选中1名男生和1名女生的概率.
16.(本小题满分8分)
屏风是一种古老的家具,它作为一种灵活的空间元素、装饰元素和设计元素,具有实用和艺术欣赏两方面的功能,能通过自身形状、色彩、质地、图案等特质融于丰富多元的现代空间环境,传达着新中式的意味,演绎出中国传统文化韵味,因此至今仍然被广泛地运用.小曦在房间墙角摆放了一架双面屏风,俯视图如图所示,两面屏风与墙角围成了一个独立空间用来堆放杂物,经测量,,请算出这个独立空间的面积.(结果精确到.参考数据:,)
17.(本小题满分10分)
如图,在中,,与相切于点,点为上一点,平分,和分别与相交于点,于点.
(1)求证:是的切线;
(2)若,的半径为,求的长.
18.(本小题满分10分)
如图,在平面直角坐标系中,一次函数的图象与坐标轴交于点A,B,与反比例函数的图象交于点,D是反比例函数图象上的一个动点,过点向轴作垂线与一次函数图象交于点,其中点的坐标为.
(1)求反比例函数的表达式;
(2)连接,当的面积等于面积的2倍时,求点的坐标;
(3)若P是x轴上的一个动点,连接,当与相似时,求点D的纵坐标.
B卷(共50分)
一、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)
19.已知非零实数a,b满足,则__________.
20.已知一元二次方程的一个根为,则的值为__________.
21.“不倒翁”玩具的主视图如图所示,分别与不倒翁底部所在的相切于点A,B,若的半径为,,则劣弧的长为__________.(结果保留)
22.一个直角三角形的边长都是整数,则称这种直角三角形为“完美勾股三角形”,k为其面积和周长的比值.当时,满足条件的“完美勾股三角形”的周长为__________;当时,若存在“完美勾股三角形”,则__________.
23.如图,在正方形中,是的中点,是边上一动点,将沿翻折得,连接,在左侧有一点,使得为等腰直角三角形,且,连接.若正方形的边长为6,则的最小值为__________.
二、解答题(本大题共3个小题,共30分,解答过程写在答题卡上)
24.(本小题满分8分)
2024年世界园艺博览会将在成都举行,某社区决定采购甲、乙两种盆栽美化环境,若购买20盆甲种盆栽和10盆乙种盆栽,则需要130元;若购买30盆甲种盆栽和20盆乙种盆栽,则需要220元.
(1)甲、乙两种盆栽的单价各是多少元?
(2)若该社区联合附近社区购买甲、乙两种盆栽共1000盆,设购买m盆()乙种盆栽,总费用为W元,请你帮社区设计一种购买方案,使总花费最少,并求出最少费用.
25.(本小题满分10分)
如图,在平面直角坐标系中,已知一抛物线经过原点,与轴交于另一点,顶点坐标为,过点的直线与抛物线交于点B,C,且点在点的左侧.
(1)求抛物线的函数表达式;
(2)连接,当的面积与的面积之比为1:2时,求直线的函数表达式;
(3)若有直线,点到直线的距离为,点到直线的距离为,求证:.
26.(本小题满分12分)
如图,已知为等边三角形,D,E分别是边上一点,与相交于点,点是射线上一点,且,与相交于点.
(1)求的度数;
(2)求证:是的中点;
(3)若,,求的边长.
同课章节目录
