高数必修2 第七章复数章末小结复习课（28页ppt）

(共28张PPT)
第七章
复 数章末复习小结课
人教A版（2019)
知识复习
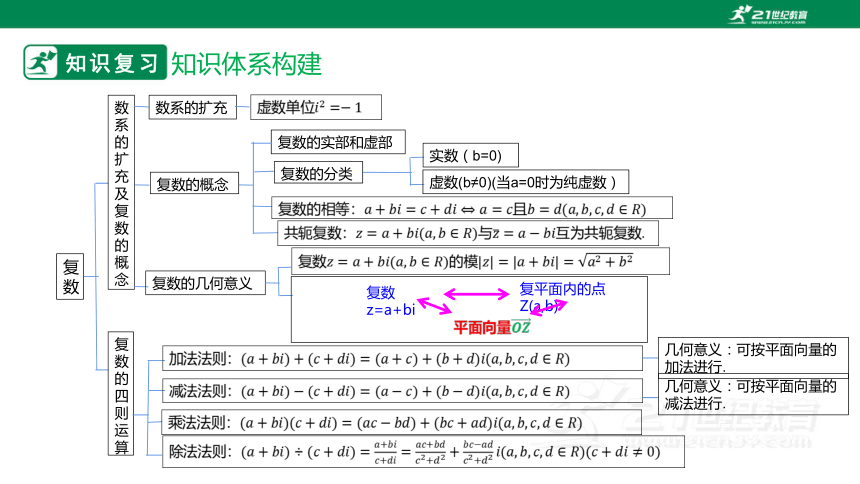
知识体系构建
复数
数系的扩充及复数的概念
复数的四则运算
数系的扩充
虚数单位
复数的概念
复数的几何意义
复数的实部和虚部
复数的分类
复数的相等：
实数（b=0)
虚数(b≠0)(当a=0时为纯虚数）
共轭复数：互为共轭复数.
复数的模
复数z=a+bi
复平面内的点Z(a,b)
平面向量
加法法则：
几何意义：可按平面向量的加法进行.
减法法则：
几何意义：可按平面向量的减法进行.
乘法法则：
除法法则：
题型探究
题型1：复数的概念　
【例1】⑴(2022全国乙理）已知 ，且 ，其中为实数，则( )
A. B.
C. D.
解：
⑴∵，∴ii,,,,,,,,,,,,,caaaaaa,,,,,p
∴
由复数相等条件，得
复数的概念是掌握复数的基础，如虚数、纯虚数、复数相等、复数的模等.有关复数的题目不同于实数，应注意根据复数的相关概念解答.
,解得
故选A.
A
题型探究
题型1：复数的概念　
【例1】⑵已知z＝lg(m2－2m－2)＋(m2＋3m＋2)i，试求实数m的取值，使
①z是实数； ②z是纯虚数.
解：
①∵z是实数，ii,,,,,,,,,,,,,caaaaaa,,,,,p
∴
∴当时，z是实数.
解得，
∴当时，z是纯虚数.
②∵z是纯虚数，ii,,,,,,,,,,,,,caaaaaa,,,,,p
∴，解得,
题型探究
题型1：复数的概念　
处理复数概念问题的两个注意点
(1)当复数不是a＋bi(a，b∈R)的形式时，要通过变形化为a＋bi的形式，以便确定其实部和虚部.
(2)求解时，要注意实部和虚部本身对变量的要求，否则容易产生增根.
初试身手
1.⑴已知i是虚单位，,则“”是“”的（ ）
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
⑵已知z1＝m2－3m＋m2i，z2＝4＋(5m＋6)i，其中m为实数，i为虚数单位，若z1－z2＝0，则m的值为______.
解：
⑴当时，;
则“”是“”充分不必要条件，应选A.
反之，,
解得，
∴.
A
题型1：复数的概念　
初试身手
1.⑴已知i是虚单位，,则“”是“”的（ ）
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
⑵已知z1＝m2－3m＋m2i，z2＝4＋(5m＋6)i，其中m为实数，i为虚数单位，若z1－z2＝0，则m的值为______.
解：
⑵∵z1－z2＝0, ∴z1=z2
即,
解得.
∴.
A
题型1：复数的概念　
-1
题型探究
【例2】 ⑴(2023全国甲文)=（ ）
A.-1 B. 1 C.1-i D. 1+i
⑵(2023天津）已知i为虚单位，化简的结果为 .
解：
⑴.
⑵
题型2：复数四则运算　
.
故选C.
C
4+i
题型探究
【例2】⑶计算.
解：
⑶
.
.
.
题型2：复数四则运算　
题型探究
题型2：复数的四则运算　
进行复数代数运算的策略
(1)复数代数运算的基本思路就是应用运算法则进行计算.
(2)在复数的四则运算中，将含有虚数单位i的看作一类同类项，不含i的看作另一类同类项，分别合并即可，但要注意把i的幂写成最简形式.
常用特殊公式：
⑴.
⑵.
复数运算是本章的重要内容，是高考考查的重点和热点，一般以复数的乘法和除法运算为主.
初试身手
2.⑴(2023甲卷理)若复数,则=( )
A.-1 B.0 C.1 D.2
⑵(2023乙卷理)设,则=（ ）
A.1-2i B.1+2i C.2-i D.2+i
解：
⑴∵,
∴
∴,解得.
故选C.
C
题型2：复数的四则运算　
初试身手
2.⑴(2023甲卷理)若复数,则=( )
A.-1 B.0 C.1 D.2
⑵(2023乙卷理)设,则=（ ）
A.1-2i B.1+2i C.2-i D.2+i
解：
∴,
∴
.
故选B.
B
题型2：复数的四则运算　
⑵∵,
题型探究
解:
∴,
∴ ,
故选A.
【例3】⑴（2023新高考Ⅰ）已知,则=( )
A.-i B.i C.0 D.1
⑵(2023全国）已知,则=( )
A. B. C. D.
题型3：共轭复数、复数的模　
⑴
.
A
题型探究
解:
,
故选B.
【例3】⑴（2023新高考Ⅰ）已知,则=( )
A.-i B.i C.0 D.1
⑵(2023全国）已知,则=( )
A. B. C. D.
题型3：共轭复数、复数的模　
⑵∵,
∴
B
∴.
题型探究
题型3：共轭复数、复数的模
共轭复数、复数的模有关性质
设,
⑴;
⑵;
⑶;
⑷.
&3& 化复为实，利用复数模的定义将复数模的条件转化为其实、虚部满足的条件，是一种复数问题实数化的思想.根据复数模的意义，可以简化计算.
初试身手
3.⑴(2022新高考Ⅰ)若,则=( )
A.-2 B.-1 C.1 D.2
⑵(2022甲卷文）若z=1+i,则=( )
A. B. C. D.
解:
⑴∵
即z=1+i,
∴,
∴.
⑵∵z=1+i，∴ .
.
∴.故选D.
则选D.
∴.
题型3：共轭复数、复数的模
D
D
题型探究
【例4】⑴（2023新高考Ⅱ）在复平面内， 对应的点位于（ ）
A. 第一象限 B. 第二象限 C. 第三象限 D.第四象限
⑵若复数z满足(i为虚单位），则z在复平面内对应图形的面积为 .
题型4：复数的几何意义及其应用　
解:
⑴∵.
∴z在复平面内对应图形的面积为.
∴在复平面内， 对应的点为（6,8），位于第一象限.
⑵∵满足的z在复平面内对应的图形是以圆心为（0,1），半径为的圆上及圆内所有点（圆盘）（如图）.
则选A.
A
x
O
y
题型探究
【例4】⑶已知复数z1＝2＋3i，z2＝，z3＝1－4i，它们在复平面上所对应的点分别为A，B，C.若，则＝______，＝______..
解:
⑶∵ ,
∴.
即.
∴.
-10
-3
题型4：复数的几何意义及其应用　
题型探究
1.复平面
题型4：复数的几何意义及其应用　
2.复数的几何意义：
复数z=a+bi
复平面内的点Z(a,b)
一 一对应
平面向量
一 一对应
一 一对应
3. 复数加法的几何意义
O
Z
Z1(a,b)
Z2(c,d)
y
x
4.复数减法的几何意义
初试身手
4.⑴(2019全国）复数在复平面内对应的点在（ ）
A. 第一象限 B. 第二象限 C. 第三象限 D.第四象限
⑵（2016上海）在复平面上，满足的复数z所对应的点的轨迹是（ ）
A.两个点 B. 一条线段 C.两条直线 D.一个圆
解：
⑴∵,
∴z在复平面内对应的点为,在第三象限.
则选D.
⑵∵的复数z所对应的点的轨迹是以点（1,0）为圆心，4为半径的圆(如图）.
则选C.
题型4：复数的几何意义及其应用　
C
x
O
y
D
题型探究
【例5】已知关于的方程 ，
⑴若方程有实数根，求锐角<和实数根；
⑵证明对任意 ，方程无纯虚数根.
解:
⑴设实数根为,则
即.
∴.
题型5：关于复数的方程问题　
.
∵，
∴.
又∵,
∴.
题型探究
【例5】已知关于的方程 ，
⑴若方程有实数根，求锐角<和实数根；
⑵证明对任意 ，方程无纯虚数根.
解:
⑵若方程存在纯虚数根，设为 ，则
即.
∴.
题型5：关于复数的方程问题　
.
∵，
∴对任意，方程无纯虚数根.
∵此方程组无实数解,
题型探究
题型5：关于复数的方程问题　
1.解关于复数的方程的依据是复数相等的条件，由此建立方程（组）求解.
2.在复数范围内解实系数一元二次方程
⑴配方法；
⑵求根公式法.
实系数一元二次方程的求根公式为：
当Δ≥0时，;
当Δ＜0时， .
初试身手
5.在复数范围内解方程：
解:
方程的二次项系数为1，配方，得.
,
题型5：关于复数的方程问题　
由Δ＜０，知 ，
可得.
则原方程的根为i.
作业布置
作业： p94-95 复习参考题7 第1，2，4，5，6，7，9题.
尽情享受学习数学的快乐吧！
我们下节课再见！
谢谢
21世纪教育网（www.21cnjy.com)
中小学教育资源网站
兼职招聘：
https://www.21cnjy.com/recruitment/home/admin