1.3.1 不等式的性质 课件(共21张PPT) 2023-2024学年高一数学北师大版(2019)必修一
文档属性
| 名称 | 1.3.1 不等式的性质 课件(共21张PPT) 2023-2024学年高一数学北师大版(2019)必修一 |  | |
| 格式 | pptx | ||
| 文件大小 | 289.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 21:05:22 | ||
图片预览








文档简介
(共21张PPT)
1.3.1 不等式的性质
新授课
1.能用作差法判断实数(或代数式)的大小.
2.掌握不等式的基本性质,会运用基本性质比较大小.
在生活中,存在着形形色色的数量关系,既有相等关系,又有不等关系.在数学中,用不等式表示不等关系.
请思考:生活中为什么糖水中加的糖越多越甜呢
将其转化为数学问题:b克糖水中含有a克糖(b>a),若再加入m(m>0)克糖,则糖水更甜了,为什么
分析:起初糖水浓度为 ,加入m克糖后的糖水浓度为 ,只要证
即可,怎么证呢
实数a、b大小比较的依据
如果a-b是正数,那么a>b
如果a-b等于0,那么a=b
如果a-b是负数,那么aa-b>0 a>b
a-b=0 a=b
a-b<0 a知识点1:实数(代数式)的大小比较
结论:确定任意两个实数a,b的大小关系,只需确定它们的差a-b与0的大小关系.
思考:比较两个实数的大小可以采取什么办法?
例1. 试比较(x+1)(x+5)与(x+3)2的大小.
解:因为(x+1)(x+5)-(x+3)2
=(x2+6x+5)-(x2+6x+9)
=-4<0,
所以(x+1)(x+5)<(x+3)2.
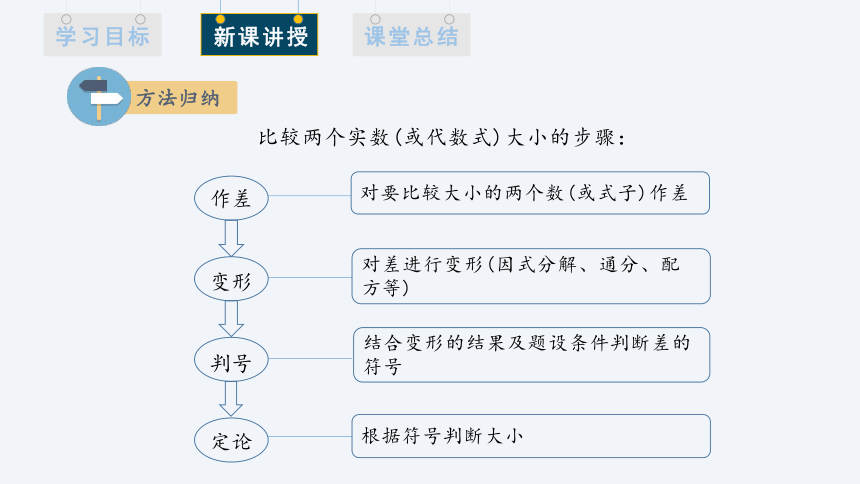
方法归纳
比较两个实数(或代数式)大小的步骤:
作差
对要比较大小的两个数(或式子)作差
变形
对差进行变形(因式分解、通分、配方等)
判号
结合变形的结果及题设条件判断差的符号
定论
根据符号判断大小
练一练
1.比较(x-3)2与(x-2)(x-4)的大小.
练一练
解:(x-3)2-(x-2)(x-4)
=x2-6x+9-x2+6x-8
=1>0
所以(x-3)2>(x-2)(x-4).
回顾:在初中的学习中,你还记得不等式有哪些基本性质吗?
知识点2:不等式的基本性质
性质1 如果a>b,b>c,那么a>c.
性质2 若a>b,则a±c>b±c.
性质3 若a>b,c>0,则ac>bc(或 );
若 a>b,c<0 ,则ac思考:根据前面比较实数大小的方法,你能证明上述不等式吗?
分析 要证a>c,只需证a-c>0.
证明:因为a>b,且b>c,所以a-b>0,b-c>0,
从而a-c=(a-b)+(b-c)>0,即a>c.
性质1
如果a>b,b>c,那么a>c.(传递性)
分析 要证a+c>b+c,只需证(a+c)-(b+c)>0.
证明: 因为a>b,所以a-b>0,
所以(a+c)-(b+c)=a-b>0,即a+c>b+c.
性质2
如果a>b,那么a+c>b+c.(可加性)
分析 (1)要证ac>bc,只需证ac-bc>0.
证明: (1)因为a>b,所以a-b>0.
又因为c>0,所以(a-b)c>0,ac-bc>0,即ac>bc.
试用(1)的方法完成(2)的证明.
(可乘性)
性质3
(1)如果a>b,c>0,那么ac>bc;
(2)如果a>b,c<0,那么ac思考:由该性质可得ac>bc a>b吗?
例2. 试证明:若00,则
又a0.
因此
证明:
又b>0,m>0,故
练一练
1.试证明:若0因此
故
又0证明:
证明:因为a>b,所以a+c>b+c.
又因为c>d,所以b+c>b+d.
由不等式的性质1,得a+c>b+d.
性质4
如果a>b,c>d,那么a+c>b+d.(同向可加性)
性质拓展
想一想:当c=d时,结合前面所学的性质,你发现了什么?
实际上,性质2和性质4可以合并在一起表达为:如果a>b,c≥d,那么a+c>b+d.
证明 (1)因为a>b,c>0,所以ac>bc.
又因为c>d,b>0,所以bc>bd.
由不等式的性质1,得ac>bd.
试用(1)的方法完成(2)的证明.
性质5
(1)如果a>b>0,c>d>0,那么ac>bd.
(2)如果a>b>0,c特殊地,当a>b>0时,an>bn,其中n∈N+,n≥2.
注意:该性质不能逆推,
如ac>bd a>b,c>d.
当 时,可得 ,即ab>0矛盾.
当 时,可得 ,即a=b与已知条件a>b>0矛盾.
所以 不成立,即
性质6
当a>b>0,,其中n∈N+,n≥2
以上不等式的性质是解决不等式问题的基本依据.
(反证法)
证明: 假设
③
例3 . 给出下列结论:
①若ac>bc,则a>b; ②若a③若 <0,则a>b; ④若a>b,c>d,则a-c>b-d;
⑤若a>b,c>d,则ac>bd.
其中正确结论的序号是______.
判断不等式是否成立的方法:
(1)运用不等式的性质判断.要注意不等式成立的条件,不要弱化条件,尤其是不能凭想象捏造性质.
(2)特殊值法.取特殊值时,要遵循如下原则:一是满足题设条件;
二是取值要简单,便于验证计算.
归纳总结
练一练
1.若0A.1-a<1-b B.
C.a2>b2 D.
B
例4. (1)已知a>b,ab>0,求证:<;
(2)已知a>b,cb-d.
证明: (1)因为ab>0,所以 >0.
又因为a>b,所以由不等式的性质3,得 .即 .
(2)因为c-d.
又因为a>b,所以由不等式的性质4,得a+(-c)>b+(-d),即a-c>b-d.
根据今天所学,回答下列问题:
(1)怎样比较两个实数(代数式)的大小?
(2)不等式的基本性质都有哪些?
1.3.1 不等式的性质
新授课
1.能用作差法判断实数(或代数式)的大小.
2.掌握不等式的基本性质,会运用基本性质比较大小.
在生活中,存在着形形色色的数量关系,既有相等关系,又有不等关系.在数学中,用不等式表示不等关系.
请思考:生活中为什么糖水中加的糖越多越甜呢
将其转化为数学问题:b克糖水中含有a克糖(b>a),若再加入m(m>0)克糖,则糖水更甜了,为什么
分析:起初糖水浓度为 ,加入m克糖后的糖水浓度为 ,只要证
即可,怎么证呢
实数a、b大小比较的依据
如果a-b是正数,那么a>b
如果a-b等于0,那么a=b
如果a-b是负数,那么a
a-b=0 a=b
a-b<0 a
结论:确定任意两个实数a,b的大小关系,只需确定它们的差a-b与0的大小关系.
思考:比较两个实数的大小可以采取什么办法?
例1. 试比较(x+1)(x+5)与(x+3)2的大小.
解:因为(x+1)(x+5)-(x+3)2
=(x2+6x+5)-(x2+6x+9)
=-4<0,
所以(x+1)(x+5)<(x+3)2.
方法归纳
比较两个实数(或代数式)大小的步骤:
作差
对要比较大小的两个数(或式子)作差
变形
对差进行变形(因式分解、通分、配方等)
判号
结合变形的结果及题设条件判断差的符号
定论
根据符号判断大小
练一练
1.比较(x-3)2与(x-2)(x-4)的大小.
练一练
解:(x-3)2-(x-2)(x-4)
=x2-6x+9-x2+6x-8
=1>0
所以(x-3)2>(x-2)(x-4).
回顾:在初中的学习中,你还记得不等式有哪些基本性质吗?
知识点2:不等式的基本性质
性质1 如果a>b,b>c,那么a>c.
性质2 若a>b,则a±c>b±c.
性质3 若a>b,c>0,则ac>bc(或 );
若 a>b,c<0 ,则ac
分析 要证a>c,只需证a-c>0.
证明:因为a>b,且b>c,所以a-b>0,b-c>0,
从而a-c=(a-b)+(b-c)>0,即a>c.
性质1
如果a>b,b>c,那么a>c.(传递性)
分析 要证a+c>b+c,只需证(a+c)-(b+c)>0.
证明: 因为a>b,所以a-b>0,
所以(a+c)-(b+c)=a-b>0,即a+c>b+c.
性质2
如果a>b,那么a+c>b+c.(可加性)
分析 (1)要证ac>bc,只需证ac-bc>0.
证明: (1)因为a>b,所以a-b>0.
又因为c>0,所以(a-b)c>0,ac-bc>0,即ac>bc.
试用(1)的方法完成(2)的证明.
(可乘性)
性质3
(1)如果a>b,c>0,那么ac>bc;
(2)如果a>b,c<0,那么ac
例2. 试证明:若0
又a
因此
证明:
又b>0,m>0,故
练一练
1.试证明:若0
故
又0
证明:因为a>b,所以a+c>b+c.
又因为c>d,所以b+c>b+d.
由不等式的性质1,得a+c>b+d.
性质4
如果a>b,c>d,那么a+c>b+d.(同向可加性)
性质拓展
想一想:当c=d时,结合前面所学的性质,你发现了什么?
实际上,性质2和性质4可以合并在一起表达为:如果a>b,c≥d,那么a+c>b+d.
证明 (1)因为a>b,c>0,所以ac>bc.
又因为c>d,b>0,所以bc>bd.
由不等式的性质1,得ac>bd.
试用(1)的方法完成(2)的证明.
性质5
(1)如果a>b>0,c>d>0,那么ac>bd.
(2)如果a>b>0,c
注意:该性质不能逆推,
如ac>bd a>b,c>d.
当 时,可得 ,即a
当 时,可得 ,即a=b与已知条件a>b>0矛盾.
所以 不成立,即
性质6
当a>b>0,,其中n∈N+,n≥2
以上不等式的性质是解决不等式问题的基本依据.
(反证法)
证明: 假设
③
例3 . 给出下列结论:
①若ac>bc,则a>b; ②若a
⑤若a>b,c>d,则ac>bd.
其中正确结论的序号是______.
判断不等式是否成立的方法:
(1)运用不等式的性质判断.要注意不等式成立的条件,不要弱化条件,尤其是不能凭想象捏造性质.
(2)特殊值法.取特殊值时,要遵循如下原则:一是满足题设条件;
二是取值要简单,便于验证计算.
归纳总结
练一练
1.若0
C.a2>b2 D.
B
例4. (1)已知a>b,ab>0,求证:<;
(2)已知a>b,c
证明: (1)因为ab>0,所以 >0.
又因为a>b,所以由不等式的性质3,得 .即 .
(2)因为c
又因为a>b,所以由不等式的性质4,得a+(-c)>b+(-d),即a-c>b-d.
根据今天所学,回答下列问题:
(1)怎样比较两个实数(代数式)的大小?
(2)不等式的基本性质都有哪些?
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
