1.4.3 一元二次不等式的应用 课件(共10张PPT) 2023-2024学年高一数学北师大版(2019)必修一
文档属性
| 名称 | 1.4.3 一元二次不等式的应用 课件(共10张PPT) 2023-2024学年高一数学北师大版(2019)必修一 |

|
|
| 格式 | pptx | ||
| 文件大小 | 278.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-23 16:01:42 | ||
图片预览




文档简介
(共10张PPT)
1.4.3 一元二次不等式的应用
新授课
1. 能运用一元二次不等式构建数学模型求解实际问题.
回顾:说说求解一元二次不等式的步骤是什么?
(1)检查a 的符号;
(2)计算 的值;
(3)画出二次函数的图象;
(4)结合图象得出不等式的解集.
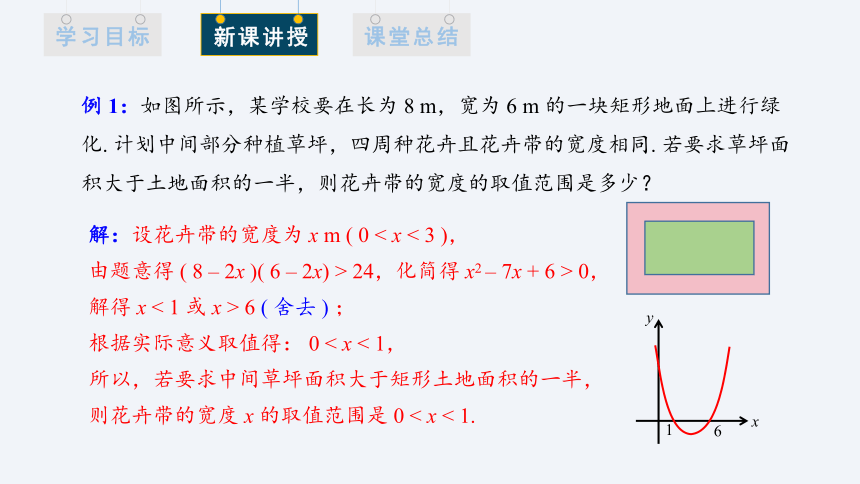
例 1:如图所示,某学校要在长为 8 m,宽为 6 m 的一块矩形地面上进行绿化. 计划中间部分种植草坪,四周种花卉且花卉带的宽度相同. 若要求草坪面积大于土地面积的一半,则花卉带的宽度的取值范围是多少?
解:设花卉带的宽度为 x m ( 0 < x < 3 ),
由题意得 ( 8 – 2x )( 6 – 2x) > 24,化简得 x2 – 7x + 6 > 0,
解得 x < 1 或 x > 6 ( 舍去 ) ;
根据实际意义取值得: 0 < x < 1,
所以,若要求中间草坪面积大于矩形土地面积的一半,
则花卉带的宽度 x 的取值范围是 0 < x < 1.
1
y
x
6
方法总结
利用不等式解决实际问题的一般步骤:
(1)选取合适的字母表示题中的未知数;
(2)由题中给出的不等关系,列出关于未知数的不等式(组);
(3)求解所列出的不等式(组);
(4)结合题目的实际意义确定答案,即结果取值需考虑实际意义.
1. 某家车辆制造厂引进了一条摩托车整车装配流水线,已知这条流水线生产的摩托车数量x (单位:辆) 与创造的价值y (单位:元) 之间有如下的关系:y = – 20x2 + 2200x.若这家工厂希望在一个星期内利用这条流水线创收 60 000 元以上,则在一个星期内大约应该生产多少辆摩托车?
解:根据题意得:– 20x2 + 2200x > 60000,整理得:x2 – 110x + 3000 < 0;
方程 x2 – 110x + 3000 = 0, = 100 > 0,有两个相等实根 x1 = 50,x2 = 60;
画出二次函数 y = x2 – 110x + 3000 的图象,结合图象得不等式 x2 – 110x + 3000 < 0 的解集为{ x | 50 < x < 60 },从而原不等式的解集为{ x | 50 < x < 60 }.
50
y
x
60
y = x2 – 110x + 3000
练一练
思考:求出不等式的解集 { x | 50 < x < 60 } 后,应该如何取值才合理?
因为摩托车只能整辆才算产出,故 x 只能取整数值;
所以当这条流水线在一周内生产的摩托车数量在 51 ~ 59 辆时,这家工厂才能够获得 60000 元以上的收益.
例 2 :某种汽车在水泥路面上的刹车距离 s (单位:m) 和汽车刹车前的车速v (单位:km/h) 之间有如下关系:;刹车距离是指汽车刹车后由于惯性往前滑行的距离. 在一次交通事故中,测得这种车的刹车距离大于 39.5 m,那么这辆汽车刹车前的车速至少为多少 (精确到 1 km/h)?
解:根据题意得: > 39.5,整理得:v2 + 9v – 7110 > 0;
画出 s = v2 + 9v – 7110 图象,得解集为 { v | v < v1 或 v > v2 },从而原不等式的解集为{ v | v < v1 或 v > v2 };
因为车速 v > 0,所以取 v > v2,而 79.9 < v2 < 80,故这辆汽车刹车前的车速至少为 80 km/h.
v1
s
v
v2
对于方程 v2 + 9v – 7110 = 0, > 0,有两相等实根 , ;
2. 甲厂以 x 千克/时的速度匀速生产某种产品 (生产条件要求1 ≤ x ≤ 10),每小时可获得利润 元. 要使生产该产品 2 小时获得的利润不低于 3000 元,求 x 的取值范围.
练一练
解:由题可知: ,化简可得 5x2 – 14x – 3 ≥ 0,
对于方程 5x2 – 14x – 3 = 0 有两个实数根 ,x2 ≥ 3,
结合函数图象可得原不等式解集 或 x2 ≥ 3,
又因为 1 ≤ x ≤ 10,所以 3 ≤ x ≤ 10.
y
x
3
根据今天所学,回答下列问题:
1. 回忆用不等式解决实际问题的一般步骤;
2. 用一元二次不等式解决实际问题时应注意什么?
1.4.3 一元二次不等式的应用
新授课
1. 能运用一元二次不等式构建数学模型求解实际问题.
回顾:说说求解一元二次不等式的步骤是什么?
(1)检查a 的符号;
(2)计算 的值;
(3)画出二次函数的图象;
(4)结合图象得出不等式的解集.
例 1:如图所示,某学校要在长为 8 m,宽为 6 m 的一块矩形地面上进行绿化. 计划中间部分种植草坪,四周种花卉且花卉带的宽度相同. 若要求草坪面积大于土地面积的一半,则花卉带的宽度的取值范围是多少?
解:设花卉带的宽度为 x m ( 0 < x < 3 ),
由题意得 ( 8 – 2x )( 6 – 2x) > 24,化简得 x2 – 7x + 6 > 0,
解得 x < 1 或 x > 6 ( 舍去 ) ;
根据实际意义取值得: 0 < x < 1,
所以,若要求中间草坪面积大于矩形土地面积的一半,
则花卉带的宽度 x 的取值范围是 0 < x < 1.
1
y
x
6
方法总结
利用不等式解决实际问题的一般步骤:
(1)选取合适的字母表示题中的未知数;
(2)由题中给出的不等关系,列出关于未知数的不等式(组);
(3)求解所列出的不等式(组);
(4)结合题目的实际意义确定答案,即结果取值需考虑实际意义.
1. 某家车辆制造厂引进了一条摩托车整车装配流水线,已知这条流水线生产的摩托车数量x (单位:辆) 与创造的价值y (单位:元) 之间有如下的关系:y = – 20x2 + 2200x.若这家工厂希望在一个星期内利用这条流水线创收 60 000 元以上,则在一个星期内大约应该生产多少辆摩托车?
解:根据题意得:– 20x2 + 2200x > 60000,整理得:x2 – 110x + 3000 < 0;
方程 x2 – 110x + 3000 = 0, = 100 > 0,有两个相等实根 x1 = 50,x2 = 60;
画出二次函数 y = x2 – 110x + 3000 的图象,结合图象得不等式 x2 – 110x + 3000 < 0 的解集为{ x | 50 < x < 60 },从而原不等式的解集为{ x | 50 < x < 60 }.
50
y
x
60
y = x2 – 110x + 3000
练一练
思考:求出不等式的解集 { x | 50 < x < 60 } 后,应该如何取值才合理?
因为摩托车只能整辆才算产出,故 x 只能取整数值;
所以当这条流水线在一周内生产的摩托车数量在 51 ~ 59 辆时,这家工厂才能够获得 60000 元以上的收益.
例 2 :某种汽车在水泥路面上的刹车距离 s (单位:m) 和汽车刹车前的车速v (单位:km/h) 之间有如下关系:;刹车距离是指汽车刹车后由于惯性往前滑行的距离. 在一次交通事故中,测得这种车的刹车距离大于 39.5 m,那么这辆汽车刹车前的车速至少为多少 (精确到 1 km/h)?
解:根据题意得: > 39.5,整理得:v2 + 9v – 7110 > 0;
画出 s = v2 + 9v – 7110 图象,得解集为 { v | v < v1 或 v > v2 },从而原不等式的解集为{ v | v < v1 或 v > v2 };
因为车速 v > 0,所以取 v > v2,而 79.9 < v2 < 80,故这辆汽车刹车前的车速至少为 80 km/h.
v1
s
v
v2
对于方程 v2 + 9v – 7110 = 0, > 0,有两相等实根 , ;
2. 甲厂以 x 千克/时的速度匀速生产某种产品 (生产条件要求1 ≤ x ≤ 10),每小时可获得利润 元. 要使生产该产品 2 小时获得的利润不低于 3000 元,求 x 的取值范围.
练一练
解:由题可知: ,化简可得 5x2 – 14x – 3 ≥ 0,
对于方程 5x2 – 14x – 3 = 0 有两个实数根 ,x2 ≥ 3,
结合函数图象可得原不等式解集 或 x2 ≥ 3,
又因为 1 ≤ x ≤ 10,所以 3 ≤ x ≤ 10.
y
x
3
根据今天所学,回答下列问题:
1. 回忆用不等式解决实际问题的一般步骤;
2. 用一元二次不等式解决实际问题时应注意什么?
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
