2.2.2 函数的表示法 课件(共13张PPT) 2023-2024学年高一数学北师大版(2019)必修一
文档属性
| 名称 | 2.2.2 函数的表示法 课件(共13张PPT) 2023-2024学年高一数学北师大版(2019)必修一 |

|
|
| 格式 | pptx | ||
| 文件大小 | 184.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-23 16:24:42 | ||
图片预览




文档简介
(共13张PPT)
2.2.2 函数的表示法
新授课
1. 通过实例理解函数的三种表示方法及其特点;
2. 理解分段函数的意义,并能简单应用;
3. 能根据函数解析式画出对应的函数图象.
知识点 1:函数的三种表示方法
回顾:函数有哪几种常用的表示方法?这些方法又是怎样表示函数的?
解析法、表格法、图象法
问题 1:某种笔记本的单价是 5 元,买 x (x∈{1,2,3,4,5}) 个笔记本需要 y 元. 请用函数的解析法表示 x 与 y 的函数关系.
解:这个函数的定义域是数集{1,2,3,4,5},
用解析法可将函数 y = f (x) 表示为 y = 5x,x∈{1,2,3,4,5};
因为有定义域和对应关系就可以求出值域,故用解析法表示函数时,
只要写出对应关系和定义域即可;
思考:所有函数都能用解析法表示吗?
在实际中,一些非常明确的函数关系很难找到它的解析式,这时就要考虑使用其他方法来表示,通常有列表法、图象法.
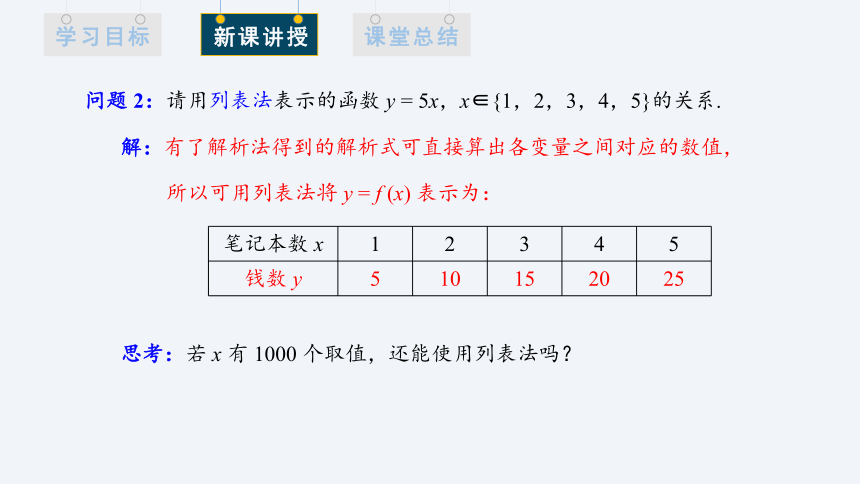
问题 2:请用列表法表示的函数 y = 5x,x∈{1,2,3,4,5}的关系.
解:有了解析法得到的解析式可直接算出各变量之间对应的数值,
所以可用列表法将 y = f (x) 表示为:
笔记本数 x 1 2 3 4 5
钱数 y 5 10 15 20 25
思考:若 x 有 1000 个取值,还能使用列表法吗?
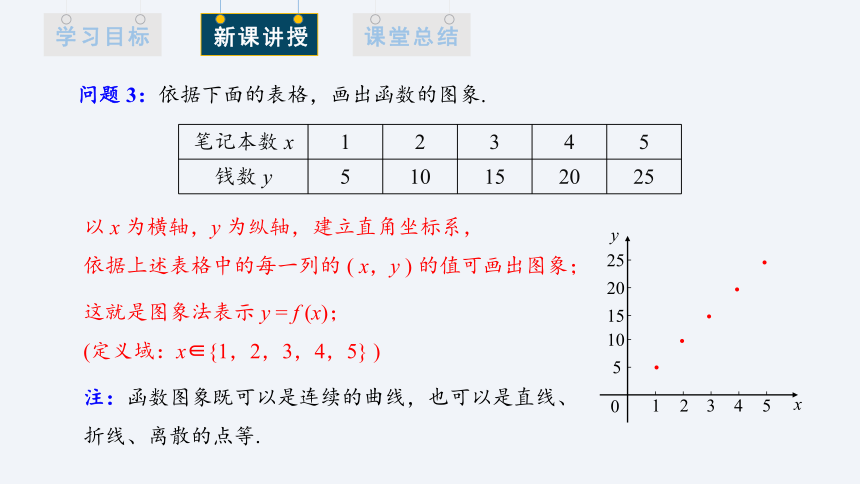
以 x 为横轴,y 为纵轴,建立直角坐标系,
依据上述表格中的每一列的 ( x,y ) 的值可画出图象;
这就是图象法表示 y = f (x);
(定义域:x∈{1,2,3,4,5} )
问题 3:依据下面的表格,画出函数的图象.
笔记本数 x 1 2 3 4 5
钱数 y 5 10 15 20 25
注:函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等.
·
·
·
·
·
25
5
10
20
15
y
0
1
2
3
4
5
x
思考:三种函数表示法各自有什么特点?
·
·
·
·
·
25
5
10
20
15
y
0
1
2
3
4
5
x
y = 5x,x∈{1,2,3,4,5}
笔记本数 x 1 2 3 4 5
钱数 y 5 10 15 20 25
归纳总结
表示法 优势 不足
解析法 能便利地利用代数工具研究其性质 某些函数关系很难用解析法表示
列表法 不用计算即可看出两个变量之间的对应值 只能表示有限个数值间的函数关系
图象法 直观地显示函数的局部变化规律 很难得到每个自变量取值对应的精确函数值
函数三种表示方法的优势及不足
以上三种函数表示法,都有其自身的局限;为了清楚地表示一个函数关系,需要有针对性地选择适当的表示方法,有时需要多种方法综合运用.
实际问题中,还常需要把函数的某种表示方法转化为另一种表示方法.
1. 写出下列函数的定义域、值域.
(1)f (x) = 3x + 5;
(2)g(x) 的图象如图所示;
(3)h(x) 与 x 的对应关系如表.
练一练
O
y
x
a1
b3
b1
b2
a2
b4
a3
a4
b5
g(x)
x 1 2 3 4 5 6 7 8
h(x) 1 8 27 64 125 216 343 512
解:(1)由解析式可知,f (x) 的定义域为R,值域为R;
(2)由图象可知,g(x) 的定义域为[a1,a2]∪[a3,a4],值域为[b4,b3];
(3)由表格可知,h(x) 的定义域为x∈{1,2,3,4,5,6,7,8},
值域为y∈{1,8,27,64,125,216,343,512}.
例 1:画出函数 y = | x | 的图象.
知识点 2:根据函数解析式画函数图象
解:由绝对值的概念,可得:
所以,函数 y = |x| 的图象如图所示.
O
3
2
1
-1
-2
-3
1
2
3
4
y
x
定义:定义域分成若干区间段,自变量 x 在不同取值区间,有不同对应关系的函数称为分段函数.
要点辨析
1. 分段函数是一个函数,而不是几个函数;处理分段函数的问题时,首先要明确自变量的取值在哪个区间,从而选取相应的对应关系;
2. 分段函数在书写的时候左边用大括号把几个对应关系括在一起,在每段对应关系表达式的后面用小括号写上相应的取值范围;
3. 分段函数的定义域是所有自变量取值区间的并集,只能写成一个集合的形式;值域是各段函数在对应自变量取值范围内值域的并集.
例 2 :设 x 为任一实数,不超过 x 的最大整数称为 x 的整数部分,记作[x],如当 x = 3.14 时,[x] = [3.14] = 3;当 x = – 3.14时,[x] = [–3.14] = – 4.
像 y = [x] 这样的函数叫作取整函数. 请画出取整函数 y = [x] 的图象.
解:依题意知函数 y = [ x ] 的定义域为R,值域为Z;
所以,函数 y = [ x ] 的图象如图所示.
O
y
x
1
2
3
4
5
-5
-4
-3
-2
-1
1
2
3
4
5
-5
-4
-3
-2
-1
结合思维导图说说你对各部分内容的理解.
函数的表示法
解析法
列表法
图象法
分段函数
定义
特点
图象解析式
2.2.2 函数的表示法
新授课
1. 通过实例理解函数的三种表示方法及其特点;
2. 理解分段函数的意义,并能简单应用;
3. 能根据函数解析式画出对应的函数图象.
知识点 1:函数的三种表示方法
回顾:函数有哪几种常用的表示方法?这些方法又是怎样表示函数的?
解析法、表格法、图象法
问题 1:某种笔记本的单价是 5 元,买 x (x∈{1,2,3,4,5}) 个笔记本需要 y 元. 请用函数的解析法表示 x 与 y 的函数关系.
解:这个函数的定义域是数集{1,2,3,4,5},
用解析法可将函数 y = f (x) 表示为 y = 5x,x∈{1,2,3,4,5};
因为有定义域和对应关系就可以求出值域,故用解析法表示函数时,
只要写出对应关系和定义域即可;
思考:所有函数都能用解析法表示吗?
在实际中,一些非常明确的函数关系很难找到它的解析式,这时就要考虑使用其他方法来表示,通常有列表法、图象法.
问题 2:请用列表法表示的函数 y = 5x,x∈{1,2,3,4,5}的关系.
解:有了解析法得到的解析式可直接算出各变量之间对应的数值,
所以可用列表法将 y = f (x) 表示为:
笔记本数 x 1 2 3 4 5
钱数 y 5 10 15 20 25
思考:若 x 有 1000 个取值,还能使用列表法吗?
以 x 为横轴,y 为纵轴,建立直角坐标系,
依据上述表格中的每一列的 ( x,y ) 的值可画出图象;
这就是图象法表示 y = f (x);
(定义域:x∈{1,2,3,4,5} )
问题 3:依据下面的表格,画出函数的图象.
笔记本数 x 1 2 3 4 5
钱数 y 5 10 15 20 25
注:函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等.
·
·
·
·
·
25
5
10
20
15
y
0
1
2
3
4
5
x
思考:三种函数表示法各自有什么特点?
·
·
·
·
·
25
5
10
20
15
y
0
1
2
3
4
5
x
y = 5x,x∈{1,2,3,4,5}
笔记本数 x 1 2 3 4 5
钱数 y 5 10 15 20 25
归纳总结
表示法 优势 不足
解析法 能便利地利用代数工具研究其性质 某些函数关系很难用解析法表示
列表法 不用计算即可看出两个变量之间的对应值 只能表示有限个数值间的函数关系
图象法 直观地显示函数的局部变化规律 很难得到每个自变量取值对应的精确函数值
函数三种表示方法的优势及不足
以上三种函数表示法,都有其自身的局限;为了清楚地表示一个函数关系,需要有针对性地选择适当的表示方法,有时需要多种方法综合运用.
实际问题中,还常需要把函数的某种表示方法转化为另一种表示方法.
1. 写出下列函数的定义域、值域.
(1)f (x) = 3x + 5;
(2)g(x) 的图象如图所示;
(3)h(x) 与 x 的对应关系如表.
练一练
O
y
x
a1
b3
b1
b2
a2
b4
a3
a4
b5
g(x)
x 1 2 3 4 5 6 7 8
h(x) 1 8 27 64 125 216 343 512
解:(1)由解析式可知,f (x) 的定义域为R,值域为R;
(2)由图象可知,g(x) 的定义域为[a1,a2]∪[a3,a4],值域为[b4,b3];
(3)由表格可知,h(x) 的定义域为x∈{1,2,3,4,5,6,7,8},
值域为y∈{1,8,27,64,125,216,343,512}.
例 1:画出函数 y = | x | 的图象.
知识点 2:根据函数解析式画函数图象
解:由绝对值的概念,可得:
所以,函数 y = |x| 的图象如图所示.
O
3
2
1
-1
-2
-3
1
2
3
4
y
x
定义:定义域分成若干区间段,自变量 x 在不同取值区间,有不同对应关系的函数称为分段函数.
要点辨析
1. 分段函数是一个函数,而不是几个函数;处理分段函数的问题时,首先要明确自变量的取值在哪个区间,从而选取相应的对应关系;
2. 分段函数在书写的时候左边用大括号把几个对应关系括在一起,在每段对应关系表达式的后面用小括号写上相应的取值范围;
3. 分段函数的定义域是所有自变量取值区间的并集,只能写成一个集合的形式;值域是各段函数在对应自变量取值范围内值域的并集.
例 2 :设 x 为任一实数,不超过 x 的最大整数称为 x 的整数部分,记作[x],如当 x = 3.14 时,[x] = [3.14] = 3;当 x = – 3.14时,[x] = [–3.14] = – 4.
像 y = [x] 这样的函数叫作取整函数. 请画出取整函数 y = [x] 的图象.
解:依题意知函数 y = [ x ] 的定义域为R,值域为Z;
所以,函数 y = [ x ] 的图象如图所示.
O
y
x
1
2
3
4
5
-5
-4
-3
-2
-1
1
2
3
4
5
-5
-4
-3
-2
-1
结合思维导图说说你对各部分内容的理解.
函数的表示法
解析法
列表法
图象法
分段函数
定义
特点
图象解析式
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
