2.3 函数的单调性和最值 第1课时 课件(共15张PPT) 2023-2024学年高一数学北师大版(2019)必修一
文档属性
| 名称 | 2.3 函数的单调性和最值 第1课时 课件(共15张PPT) 2023-2024学年高一数学北师大版(2019)必修一 |  | |
| 格式 | pptx | ||
| 文件大小 | 276.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-23 15:57:36 | ||
图片预览






文档简介
(共15张PPT)
2.3 函数的单调性和最值
第 1 课时
新授课
1. 通过具体实例,理解增函数、减函数、最值等概念;
2. 会用符号语言表达函数的单调性;
3. 能借助函数图象直观地判断函数的单调性.
知识点 1:函数的单调性
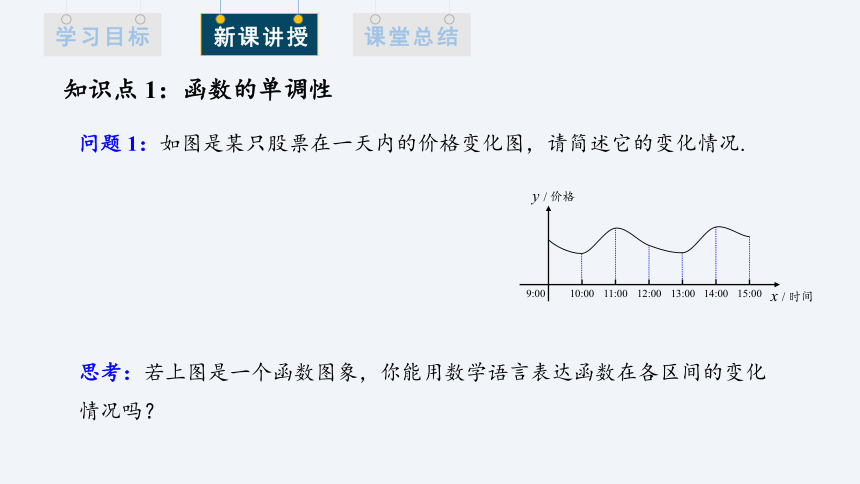
问题 1:如图是某只股票在一天内的价格变化图,请简述它的变化情况.
y / 价格
x / 时间
9:00
10:00
11:00
12:00
13:00
14:00
15:00
思考:若上图是一个函数图象,你能用数学语言表达函数在各区间的变化情况吗?
问题 2:如何描述二次函数 f (x) = x2 的单调性.
回顾:在初中阶段,我们利用函数图象探究过函数值 f (x) 随自变量 x 的变化情况,描述这种变化情况的性质就叫做函数的单调性.
① 画出函数图象,由图象可知:
即:函数 f (x) = x2 在 ( – ∞,0 ] 上是单调递减的;
在 [ 0,+ ∞ ) 上是单调递增的.
在区间 ( – ∞,0 ] 上:函数值 f (x) 随 x 的增大而减小;
在区间 [ 0,+ ∞ ) 上:函数值 f (x) 随 x 的增大而增大;
思考:怎样用数学的符号语言表达函数值 f (x) 在区间 ( – ∞,0 ] 上单调递减呢?
设函数 f (x) 的定义域为 D:
概念生成
如果 x1,x2∈D,当 x1 < x2 时,都有 f (x1) < f (x2) ,那么就称函数 f (x) 是增函数;特别地,当区间 I D 时,函数 f (x) 在区间 I 上单调递增;
如果 x1,x2∈D,当 x1 < x2 时,都有 f (x1) > f (x2) ,那么就称函数 f (x) 是减函数;特别地,当区间 I D 时,函数 f (x) 在区间 I 上单调递减;
如果函数 f (x) 在区间 I 上单调递增或单调递减,则称函数 f (x) 在区间 I 上具有单调性;此时,区间 I 为函数 f (x) 的单调区间.
f (x1)
f (x2)
f (x1)
y = f (x2)
问题 3 :函数 y = f (x) 在定义域的某区间上存在 x1,x2 满足 x1 < x2,且
f (x1) < f (x2),那么函数 y = f (x) 在该区间上一定是单调递增吗?
y
x
f (x2)
f (x1)
O
x1
x2
如右图所示,某区间上存在 x1,x2 满足 x1 < x2,且 f (x1) < f (x2),但在该区间上,函数不单调.
注意:函数单调性的概念是: f (x) 在定义域的某区间上任意 x1,x2 ,满足 x1 < x2,且 f (x1) < f (x2),则函数 y = f (x) 在该区间上一定单调递增.
例 1 :设 f (x) = ( x < 0 ),画出 f (x + 3) ( x < – 3 ) 的图象,并通过图象直观判断它的单调性.
解:依题意可知 f (x + 3) = ( x < – 3 ) ,其图象可由 f (x) = ( x < 0 ) 的图象向左平移 3 个单位得到;
O
– 4
– 1
– 2
– 3
1
–5
x
– 4
– 1
– 2
– 3
1
y
y =
由 f (x + 3) 的图象可知:
该函数在区间 ( – ∞,– 3 ) 单调递减.
练一练
1. 根据函数图象直观判断 y = | x – 2 | 的单调性.
3
2
1
4
O
1
2
y
x
解:函数 y = | x – 2 | 可以表示为 y = ,
画出该函数图象,由图可知:
该函数在 ( – ∞,2 ] 上是单调递减的;在 [ 2,+ ∞ ) 上是单调递增的.
简单函数的单调性判断步骤:
① 写出函数在各区间的解析式;② 画出函数对应区间的图象;③ 根据图象直观判断函数的单调性;④ 写出函数对应单调区间.
知识点 2:函数的最大值和最小值
观察:下面两个函数图象中,都有一个最高点,那么该如何用数学语言描述这个最高点呢?
O
x0
x
M
y
y
x
O
x0
M
问题:设函数 y = f (x) 图象上最高点的纵坐标为 M,则对函数定义域内任意自变量 x, f (x) 与 M 的大小关系如何?
(1)对任意的 x∈R 都有 f (x) ≤ 0;
(2)存在 0,使得 (0) = 0.
例如:函数 f (x) = – x2 ( x∈R ) 的图象如图:
O
1
y
x
1
-1
-1
一般地,设函数 y = f (x) 的定义域为 I :
若存在实数 M 满足: x∈I,有 f (x) ≤ M 且 x0∈I,使得 f (x0) = M;
则称 M 是函数 y = f (x) 的最大值.
概念生成
同理,若存在实数 N 满足: x∈I,有 f (x) ≥ N 且 x0∈I,使得 f (x0) = N ;
则称 N 是函数 y = f (x) 的最小值.
函数的最大值和最小值统称为最值.
例 2 :“菊花”烟花是最壮观的烟花之一. 制造时一般是期望它在达到最高点时爆裂.如果烟花距地面的高度 (单位:m) 与时间 (单位:s) 之间的关系为 h(t) = – 4.9t2 + 14.7t + 18;那么烟花冲出后什么时候是爆裂的最佳时刻?这时烟花距地面的高度又是多少 ( 精确到1 m )?
25
20
15
10
5
1
2
3
4
5
t
O
h
30
h(t) = – 4.9t2 + 14.7t + 18
解:画出函数 h(t) = – 4.9t2 + 14.7t + 18 的图象;
函数图象的顶点就是烟花上升的最高点,顶点的横坐标就是烟花爆裂的最佳时刻,纵坐标就是这时距地面的高度;
25
20
15
10
5
1
2
3
4
5
t
O
h
30
h(t) = – 4.9t2 + 14.7t + 18
所以,烟花冲出后 1.5 s 是它爆裂的最佳时刻,
这时距地面的高度是 29 m.
由二次函数的解法得,对于函数 h(t) = – 4.9t2 + 14.7t + 18 有:
当 时,函数有最大值
练一练
1. 已知函数 f (x) = x2 – 2x – 3,若 x∈[0,2],求函数 f (x) 的最值.
解:将函数 f (x) = x2 – 2x – 3 化成顶点式 f (x) = (x – 1)2 – 4;
画出该函数图象,由图可知:f (x)min = f (1) = – 4 ;
∵ f (0) – f (2) = – 3 – (22 – 2×2 – 3) = 0,
∴ f (x) max = f (0) = f (2) = – 3.
-1
-2
-3
-4
1
2
3
x
O
y
方法小结:
(1)函数最大值对应图象中的最高点,最小值对应图象中的最低点;
(2)区间端点处的最值需通过计算判断.
根据今天所学,回答下列问题:
1. 说说增函数、减函数、最值的分别是什么?
2. 什么叫函数的单调性?并说说如何借助图象判断函数的单调性?
2.3 函数的单调性和最值
第 1 课时
新授课
1. 通过具体实例,理解增函数、减函数、最值等概念;
2. 会用符号语言表达函数的单调性;
3. 能借助函数图象直观地判断函数的单调性.
知识点 1:函数的单调性
问题 1:如图是某只股票在一天内的价格变化图,请简述它的变化情况.
y / 价格
x / 时间
9:00
10:00
11:00
12:00
13:00
14:00
15:00
思考:若上图是一个函数图象,你能用数学语言表达函数在各区间的变化情况吗?
问题 2:如何描述二次函数 f (x) = x2 的单调性.
回顾:在初中阶段,我们利用函数图象探究过函数值 f (x) 随自变量 x 的变化情况,描述这种变化情况的性质就叫做函数的单调性.
① 画出函数图象,由图象可知:
即:函数 f (x) = x2 在 ( – ∞,0 ] 上是单调递减的;
在 [ 0,+ ∞ ) 上是单调递增的.
在区间 ( – ∞,0 ] 上:函数值 f (x) 随 x 的增大而减小;
在区间 [ 0,+ ∞ ) 上:函数值 f (x) 随 x 的增大而增大;
思考:怎样用数学的符号语言表达函数值 f (x) 在区间 ( – ∞,0 ] 上单调递减呢?
设函数 f (x) 的定义域为 D:
概念生成
如果 x1,x2∈D,当 x1 < x2 时,都有 f (x1) < f (x2) ,那么就称函数 f (x) 是增函数;特别地,当区间 I D 时,函数 f (x) 在区间 I 上单调递增;
如果 x1,x2∈D,当 x1 < x2 时,都有 f (x1) > f (x2) ,那么就称函数 f (x) 是减函数;特别地,当区间 I D 时,函数 f (x) 在区间 I 上单调递减;
如果函数 f (x) 在区间 I 上单调递增或单调递减,则称函数 f (x) 在区间 I 上具有单调性;此时,区间 I 为函数 f (x) 的单调区间.
f (x1)
f (x2)
f (x1)
y = f (x2)
问题 3 :函数 y = f (x) 在定义域的某区间上存在 x1,x2 满足 x1 < x2,且
f (x1) < f (x2),那么函数 y = f (x) 在该区间上一定是单调递增吗?
y
x
f (x2)
f (x1)
O
x1
x2
如右图所示,某区间上存在 x1,x2 满足 x1 < x2,且 f (x1) < f (x2),但在该区间上,函数不单调.
注意:函数单调性的概念是: f (x) 在定义域的某区间上任意 x1,x2 ,满足 x1 < x2,且 f (x1) < f (x2),则函数 y = f (x) 在该区间上一定单调递增.
例 1 :设 f (x) = ( x < 0 ),画出 f (x + 3) ( x < – 3 ) 的图象,并通过图象直观判断它的单调性.
解:依题意可知 f (x + 3) = ( x < – 3 ) ,其图象可由 f (x) = ( x < 0 ) 的图象向左平移 3 个单位得到;
O
– 4
– 1
– 2
– 3
1
–5
x
– 4
– 1
– 2
– 3
1
y
y =
由 f (x + 3) 的图象可知:
该函数在区间 ( – ∞,– 3 ) 单调递减.
练一练
1. 根据函数图象直观判断 y = | x – 2 | 的单调性.
3
2
1
4
O
1
2
y
x
解:函数 y = | x – 2 | 可以表示为 y = ,
画出该函数图象,由图可知:
该函数在 ( – ∞,2 ] 上是单调递减的;在 [ 2,+ ∞ ) 上是单调递增的.
简单函数的单调性判断步骤:
① 写出函数在各区间的解析式;② 画出函数对应区间的图象;③ 根据图象直观判断函数的单调性;④ 写出函数对应单调区间.
知识点 2:函数的最大值和最小值
观察:下面两个函数图象中,都有一个最高点,那么该如何用数学语言描述这个最高点呢?
O
x0
x
M
y
y
x
O
x0
M
问题:设函数 y = f (x) 图象上最高点的纵坐标为 M,则对函数定义域内任意自变量 x, f (x) 与 M 的大小关系如何?
(1)对任意的 x∈R 都有 f (x) ≤ 0;
(2)存在 0,使得 (0) = 0.
例如:函数 f (x) = – x2 ( x∈R ) 的图象如图:
O
1
y
x
1
-1
-1
一般地,设函数 y = f (x) 的定义域为 I :
若存在实数 M 满足: x∈I,有 f (x) ≤ M 且 x0∈I,使得 f (x0) = M;
则称 M 是函数 y = f (x) 的最大值.
概念生成
同理,若存在实数 N 满足: x∈I,有 f (x) ≥ N 且 x0∈I,使得 f (x0) = N ;
则称 N 是函数 y = f (x) 的最小值.
函数的最大值和最小值统称为最值.
例 2 :“菊花”烟花是最壮观的烟花之一. 制造时一般是期望它在达到最高点时爆裂.如果烟花距地面的高度 (单位:m) 与时间 (单位:s) 之间的关系为 h(t) = – 4.9t2 + 14.7t + 18;那么烟花冲出后什么时候是爆裂的最佳时刻?这时烟花距地面的高度又是多少 ( 精确到1 m )?
25
20
15
10
5
1
2
3
4
5
t
O
h
30
h(t) = – 4.9t2 + 14.7t + 18
解:画出函数 h(t) = – 4.9t2 + 14.7t + 18 的图象;
函数图象的顶点就是烟花上升的最高点,顶点的横坐标就是烟花爆裂的最佳时刻,纵坐标就是这时距地面的高度;
25
20
15
10
5
1
2
3
4
5
t
O
h
30
h(t) = – 4.9t2 + 14.7t + 18
所以,烟花冲出后 1.5 s 是它爆裂的最佳时刻,
这时距地面的高度是 29 m.
由二次函数的解法得,对于函数 h(t) = – 4.9t2 + 14.7t + 18 有:
当 时,函数有最大值
练一练
1. 已知函数 f (x) = x2 – 2x – 3,若 x∈[0,2],求函数 f (x) 的最值.
解:将函数 f (x) = x2 – 2x – 3 化成顶点式 f (x) = (x – 1)2 – 4;
画出该函数图象,由图可知:f (x)min = f (1) = – 4 ;
∵ f (0) – f (2) = – 3 – (22 – 2×2 – 3) = 0,
∴ f (x) max = f (0) = f (2) = – 3.
-1
-2
-3
-4
1
2
3
x
O
y
方法小结:
(1)函数最大值对应图象中的最高点,最小值对应图象中的最低点;
(2)区间端点处的最值需通过计算判断.
根据今天所学,回答下列问题:
1. 说说增函数、减函数、最值的分别是什么?
2. 什么叫函数的单调性?并说说如何借助图象判断函数的单调性?
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
