3.3.2 指数函数的图象和性质 第2课时 课件(共17张PPT) 2023-2024学年高一数学北师大版(2019)必修一
文档属性
| 名称 | 3.3.2 指数函数的图象和性质 第2课时 课件(共17张PPT) 2023-2024学年高一数学北师大版(2019)必修一 |  | |
| 格式 | pptx | ||
| 文件大小 | 594.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-23 15:59:09 | ||
图片预览




文档简介
(共17张PPT)
3.3.2 指数函数的图象和性质
第 2 课时
新授课
1.掌握指数函数的图像与性质,能运用指数函数的图象和性质解 决有关数学问题.
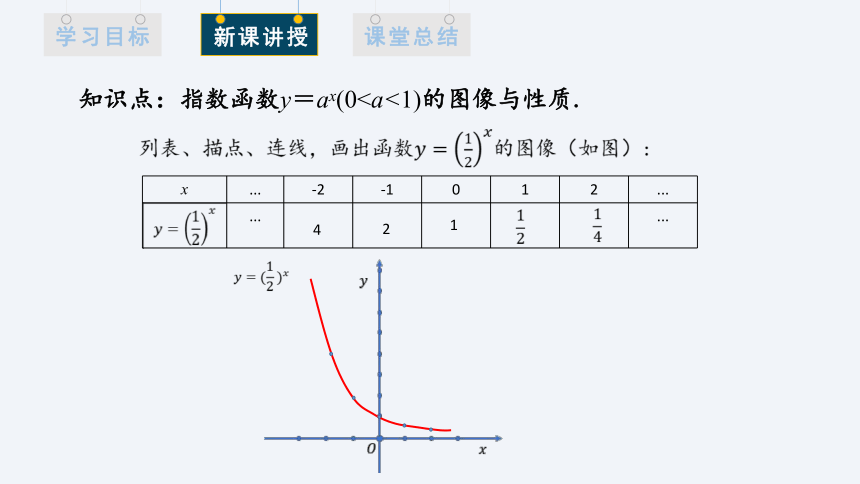
列表、描点、连线,画出函数的图像(如图):
x ... -2 -1 0 1 2 ...
... ...
知识点:指数函数y=ax(01
2
4
思考:观察图像,你能发现函数图像有什么特点?
从图象可以看出:函数的图象位于x轴的上方;从最左侧无穷远处逐渐下降,过点(0,1),继续下降,越来越逼近x轴.
由此得到函数的性质:
函数在R上是减函数,且值域是(0,+∞).
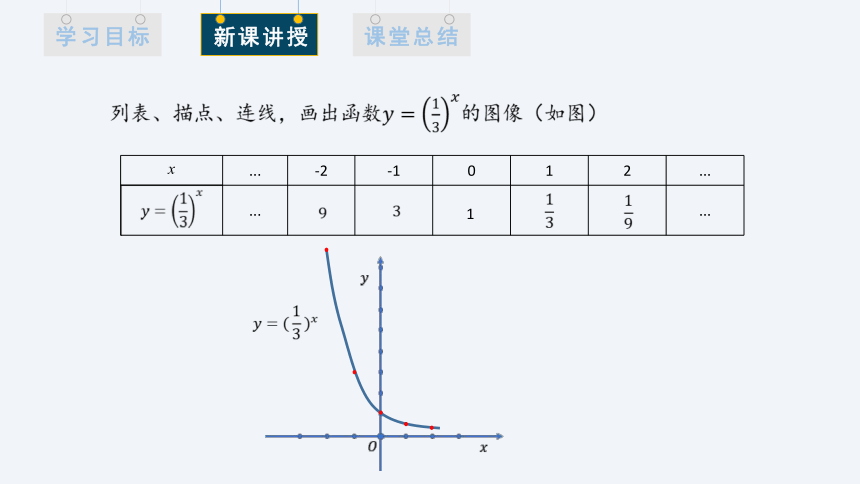
列表、描点、连线,画出函数的图像(如图)
x ... -2 -1 0 1 2 ...
... ...
1
函数的图象位于x轴的上方;从最左侧无穷远处逐渐下降,过点(0,1),继续下降,越来越逼近x轴.
由此得到函数的性质:
函数在R上是减函数,且值域是(0,+∞).
从图象可以看出:
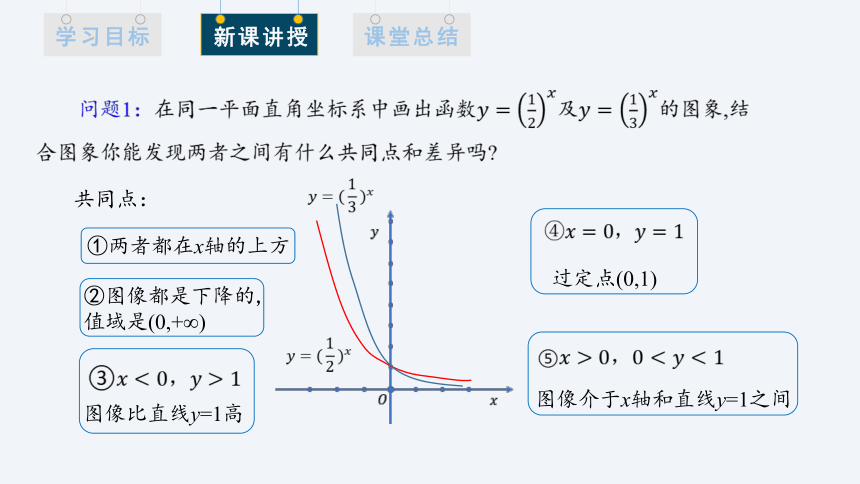
问题1:在同一平面直角坐标系中画出函数及的图象,结合图象你能发现两者之间有什么共同点和差异吗
共同点:
⑤
图像介于x轴和直线y=1之间
图像比直线y=1高
过定点(0,1)
②图像都是下降的,值域是(0,+∞)
①两者都在x轴的上方
差异:
① 在y轴左侧,即x<0,函数的图象在函数的图象上方;
② 在y轴右侧,即x>0,函数的图象在函数的图象下方.
问题2:根据上述几个函数图像的特点,你能归纳出当0指数函数y=ax在0a的范围 0图像
性质 定义域
值域
过定点
单调性
R
(0,+∞)
过定点(0,1)
在R上是减函数;
当时,;
当时,
o
(0,1)
y
x
对于函数和(0(1) 当时,
(2) 当时
(3) 当时,.
例1. 比较下列各题中两个数的大小:
(1) (2)
解:(1)因为函数,
所以;
(2) ,
所以
例2.比较下列各题中两个数的大小:
(1); (2)
解:(1)因为底数0<0.4<0.5<1,指数-5<0,
所以;
(2)因为底数0<0.4<0.5<1,指数5>0,
所以.
尝试用图像法解此题.
例3. 求下列函数的值域.
(1); (2)
解:(1)因为=2,而函数的值域是(0,+∞),
所以函数的值域为(0,+∞);
(2)因为函数=3,而函数在R上是减函数,
所以函数的值域为(0,3即(0,27].
练一练
(2)
由 所以 ;
解:(1)因为函数,
(2)因为函数,
由0.3<3.1,所以 .
(1)
1.比较下列各题中两个数的大小:
2.求下列函数的值域.
; ⑵.
解:⑴因为=8,而函数的值域是(0,+∞),
所以函数的值域为(0,+∞);
⑵因为=,而函数的值域是(0,+∞),
所以函数的值域为(0,+∞).
a>1 0图像
性质
⑸在R上是减函数;
当时,;
当时,
o
(0,1)
y
x
⑸在R上是增函数;
当时,
当时.
y
x
o
(0,1)
结合上节课所学,指数函数y=ax的图像和性质如表:
⑴定义域 R
⑵值域(0,+∞)
⑶过定点(0,1),即x=0时,y=1.
⑷当x<0时,00时,y>1.
⑷当x<0时,y>1;当x>0时,0根据今天所学,回答下列问题:
(1)指数函数有哪些性质?
(2)不同底数a对指数函数的大小有什么影响?
3.3.2 指数函数的图象和性质
第 2 课时
新授课
1.掌握指数函数的图像与性质,能运用指数函数的图象和性质解 决有关数学问题.
列表、描点、连线,画出函数的图像(如图):
x ... -2 -1 0 1 2 ...
... ...
知识点:指数函数y=ax(0
2
4
思考:观察图像,你能发现函数图像有什么特点?
从图象可以看出:函数的图象位于x轴的上方;从最左侧无穷远处逐渐下降,过点(0,1),继续下降,越来越逼近x轴.
由此得到函数的性质:
函数在R上是减函数,且值域是(0,+∞).
列表、描点、连线,画出函数的图像(如图)
x ... -2 -1 0 1 2 ...
... ...
1
函数的图象位于x轴的上方;从最左侧无穷远处逐渐下降,过点(0,1),继续下降,越来越逼近x轴.
由此得到函数的性质:
函数在R上是减函数,且值域是(0,+∞).
从图象可以看出:
问题1:在同一平面直角坐标系中画出函数及的图象,结合图象你能发现两者之间有什么共同点和差异吗
共同点:
⑤
图像介于x轴和直线y=1之间
图像比直线y=1高
过定点(0,1)
②图像都是下降的,值域是(0,+∞)
①两者都在x轴的上方
差异:
① 在y轴左侧,即x<0,函数的图象在函数的图象上方;
② 在y轴右侧,即x>0,函数的图象在函数的图象下方.
问题2:根据上述几个函数图像的特点,你能归纳出当0
性质 定义域
值域
过定点
单调性
R
(0,+∞)
过定点(0,1)
在R上是减函数;
当时,;
当时,
o
(0,1)
y
x
对于函数和(0
(2) 当时
(3) 当时,.
例1. 比较下列各题中两个数的大小:
(1) (2)
解:(1)因为函数,
所以;
(2) ,
所以
例2.比较下列各题中两个数的大小:
(1); (2)
解:(1)因为底数0<0.4<0.5<1,指数-5<0,
所以;
(2)因为底数0<0.4<0.5<1,指数5>0,
所以.
尝试用图像法解此题.
例3. 求下列函数的值域.
(1); (2)
解:(1)因为=2,而函数的值域是(0,+∞),
所以函数的值域为(0,+∞);
(2)因为函数=3,而函数在R上是减函数,
所以函数的值域为(0,3即(0,27].
练一练
(2)
由 所以 ;
解:(1)因为函数,
(2)因为函数,
由0.3<3.1,所以 .
(1)
1.比较下列各题中两个数的大小:
2.求下列函数的值域.
; ⑵.
解:⑴因为=8,而函数的值域是(0,+∞),
所以函数的值域为(0,+∞);
⑵因为=,而函数的值域是(0,+∞),
所以函数的值域为(0,+∞).
a>1 0
性质
⑸在R上是减函数;
当时,;
当时,
o
(0,1)
y
x
⑸在R上是增函数;
当时,
当时.
y
x
o
(0,1)
结合上节课所学,指数函数y=ax的图像和性质如表:
⑴定义域 R
⑵值域(0,+∞)
⑶过定点(0,1),即x=0时,y=1.
⑷当x<0时,0
⑷当x<0时,y>1;当x>0时,0
(1)指数函数有哪些性质?
(2)不同底数a对指数函数的大小有什么影响?
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
