6.2.2 分层随机抽样 课件(共15张PPT) 2023-2024学年高一数学北师大版(2019)必修一
文档属性
| 名称 | 6.2.2 分层随机抽样 课件(共15张PPT) 2023-2024学年高一数学北师大版(2019)必修一 |

|
|
| 格式 | pptx | ||
| 文件大小 | 248.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 21:14:59 | ||
图片预览





文档简介
(共15张PPT)
6.2.2 分层随机抽样
新授课
1.通过实际问题情境,理解分层随机抽样的概念.
2.掌握分层随机抽样的步骤,会利用分层随机抽样从总体中抽取样本.
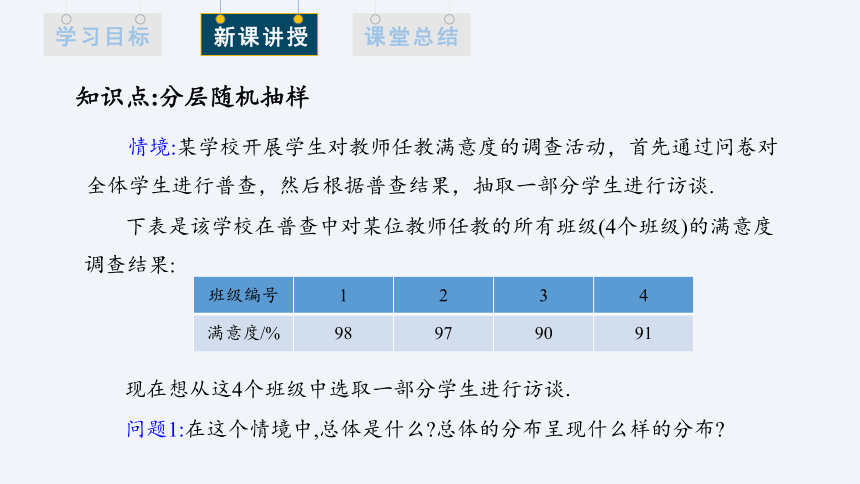
情境:某学校开展学生对教师任教满意度的调查活动,首先通过问卷对全体学生进行普查,然后根据普查结果,抽取一部分学生进行访谈.
知识点:分层随机抽样
问题1:在这个情境中,总体是什么 总体的分布呈现什么样的分布
下表是该学校在普查中对某位教师任教的所有班级(4个班级)的满意度调查结果:
班级编号 1 2 3 4
满意度/% 98 97 90 91
现在想从这4个班级中选取一部分学生进行访谈.
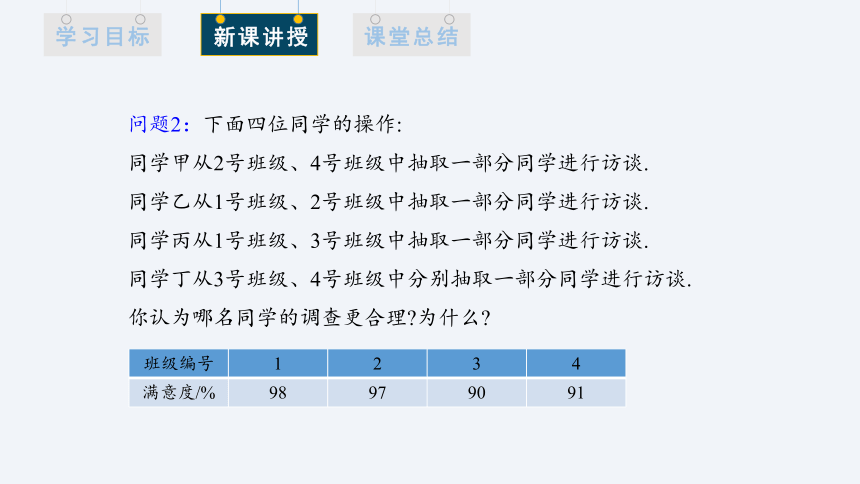
问题2:下面四位同学的操作:
同学甲从2号班级、4号班级中抽取一部分同学进行访谈.
同学乙从1号班级、2号班级中抽取一部分同学进行访谈.
同学丙从1号班级、3号班级中抽取一部分同学进行访谈.
同学丁从3号班级、4号班级中分别抽取一部分同学进行访谈.
你认为哪名同学的调查更合理 为什么
班级编号 1 2 3 4
满意度/% 98 97 90 91
某市有大、中、小型的商店共1500家,且这三种类型商店的数量之比为1:5:9.要调查全市商店的每日零售额情况,要求抽取30家商店进行调查,应当采用怎样的抽样方法?
实例分析:
问题:
(1)这个问题的总体是什么 能否用简单随机抽样进行抽样 为什么
(2)如何使样本很好地代表总体的特征
调查的总体是1500家商店的每日零售额.
不能用简单随机抽样进行抽样.原因:一是商店的数量比较多;二是大、中、小型商店的比例为1:5:9,即各类商店数量不一样,如果用简单随机抽样进行抽取,不能够使样本很好的代表总体的特征.
要使样本很好的代表总体的特征,抽取的30家商店样本应按照1:5:9的比例从大、中、小型商店中抽取.
所以,抽取 (家)大型商店, (家)中型商店,
(家)小型商店,组成样本.
概念生成
定义
适用条件
优点
分层随机抽样的概念:
样本能很好地反映总体的规律,提高对总体推断的准确性.
总体是由差异明显的几类个体构成,并且知道每一类个体
在总体中所占的百分比.
将总体按其属性特征分成互不交叉的若干类型(有时称作层),
然后在每个类型中按照所占比例随机抽取一定的个体.
例1.某地农田分布在山地、丘陵、平原、洼地不同的地形上,要对这个地区的农作物产量进行调查,应当如何抽样?
解:因为不同类型农田的产量有较大差异,所以应当采用分层随机抽样的方法,对不同类型的农田按其占总数的比例抽取样本.
归纳总结
1.使用分层随机抽样的前提:
总体可以分层,层与层之间有明显区别,而层内个体间差异较小.
2.使用分层随机抽样应遵循的原则:
(1)将相似的个体归入一类,即为一层,分层要求每层的各个个体互不交叉,即遵循不重复、不遗漏的原则;
(2)分层随机抽样为保证每个个体等可能入样,需遵循在各层中进行简单随机抽样,每层样本数量与每层个体数量的比等于样本容量与总体中个体数的比.
下列问题中,最适合用分层随机抽样抽取样本的是( )
A.从10名同学中抽取3人参加座谈会
B.某社区有300户家庭,其中高收入的家庭75户,中等收入的家庭180户,低收入的家庭45户,为了了解生活购买力的某项指标,要从中抽取一个容量为50的样本
C.从1000名工人中,抽取100人调查上班途中所用的时间
D.从生产流水线上,抽取样本检查产品质量
练一练
B
例2.某公司有1000名员工,其中50名属于高收入者,150名属于中等收入者,800名属于低收入者.要对该公司员工的具体收入情况进行调查,欲抽取100名员工,应当怎样抽样比较合理?
同理,抽取15名中等收入者、80名低收入者,再对他们的具体收入状况分别进行调查.
解:采用分层随机抽样的方法.按照该公司员工的收入水平分成三层:高收入者、中等收入者、低收入者.
高收入者为50名,占所有员工的比例为 =5%,在所抽取的100名员工中,高收入者所占的比例也应为5%,即100×5%=5,所以应抽取5名高收入者比较合理.
分层抽样的操作步骤:
分层
将总体按一定的标准分层
定比
计算各层的个体数与总体的个体数的比
定量
按各层个体数与总体的个体数的比确定各层应抽取的样本容量
抽样
在每一层进行抽样
归纳总结
某学校有在编人员200人,其中行政人员20人,教师140人,后勤人员40人.教育部门为了解学校职工对学校县管校聘改革的意见,要从中抽取20人,试确定用何种方法抽样,并写出抽样过程.
练一练
解:(1)将200人分成行政人员、教师、后勤人员三层;
(2)按照的比例确定各层抽取的人数,行政人员:20×2(人),教师:140×14(人),后勤人员:40×4(人);
(3)在各层中用简单随机抽样的方法抽取样本;
(4)将抽取的20人综合到一起,即得到一个样本容量为20的样本.
方法类别 共同特点 抽样特征 相互联系 适应范围
简单随机抽样
分层抽样
抽样过程中每个个体被抽取的可能性相等
从总体中逐个不放回抽取
将总体分成互不交叉的几层,按比例分层抽样
各层抽样时采用简单随机抽样
总体中的个体数较少
总体由差异明显的几部分组成
两种抽样方法对比:
框图结构
分层随机抽样
操作步骤
概念
应用
6.2.2 分层随机抽样
新授课
1.通过实际问题情境,理解分层随机抽样的概念.
2.掌握分层随机抽样的步骤,会利用分层随机抽样从总体中抽取样本.
情境:某学校开展学生对教师任教满意度的调查活动,首先通过问卷对全体学生进行普查,然后根据普查结果,抽取一部分学生进行访谈.
知识点:分层随机抽样
问题1:在这个情境中,总体是什么 总体的分布呈现什么样的分布
下表是该学校在普查中对某位教师任教的所有班级(4个班级)的满意度调查结果:
班级编号 1 2 3 4
满意度/% 98 97 90 91
现在想从这4个班级中选取一部分学生进行访谈.
问题2:下面四位同学的操作:
同学甲从2号班级、4号班级中抽取一部分同学进行访谈.
同学乙从1号班级、2号班级中抽取一部分同学进行访谈.
同学丙从1号班级、3号班级中抽取一部分同学进行访谈.
同学丁从3号班级、4号班级中分别抽取一部分同学进行访谈.
你认为哪名同学的调查更合理 为什么
班级编号 1 2 3 4
满意度/% 98 97 90 91
某市有大、中、小型的商店共1500家,且这三种类型商店的数量之比为1:5:9.要调查全市商店的每日零售额情况,要求抽取30家商店进行调查,应当采用怎样的抽样方法?
实例分析:
问题:
(1)这个问题的总体是什么 能否用简单随机抽样进行抽样 为什么
(2)如何使样本很好地代表总体的特征
调查的总体是1500家商店的每日零售额.
不能用简单随机抽样进行抽样.原因:一是商店的数量比较多;二是大、中、小型商店的比例为1:5:9,即各类商店数量不一样,如果用简单随机抽样进行抽取,不能够使样本很好的代表总体的特征.
要使样本很好的代表总体的特征,抽取的30家商店样本应按照1:5:9的比例从大、中、小型商店中抽取.
所以,抽取 (家)大型商店, (家)中型商店,
(家)小型商店,组成样本.
概念生成
定义
适用条件
优点
分层随机抽样的概念:
样本能很好地反映总体的规律,提高对总体推断的准确性.
总体是由差异明显的几类个体构成,并且知道每一类个体
在总体中所占的百分比.
将总体按其属性特征分成互不交叉的若干类型(有时称作层),
然后在每个类型中按照所占比例随机抽取一定的个体.
例1.某地农田分布在山地、丘陵、平原、洼地不同的地形上,要对这个地区的农作物产量进行调查,应当如何抽样?
解:因为不同类型农田的产量有较大差异,所以应当采用分层随机抽样的方法,对不同类型的农田按其占总数的比例抽取样本.
归纳总结
1.使用分层随机抽样的前提:
总体可以分层,层与层之间有明显区别,而层内个体间差异较小.
2.使用分层随机抽样应遵循的原则:
(1)将相似的个体归入一类,即为一层,分层要求每层的各个个体互不交叉,即遵循不重复、不遗漏的原则;
(2)分层随机抽样为保证每个个体等可能入样,需遵循在各层中进行简单随机抽样,每层样本数量与每层个体数量的比等于样本容量与总体中个体数的比.
下列问题中,最适合用分层随机抽样抽取样本的是( )
A.从10名同学中抽取3人参加座谈会
B.某社区有300户家庭,其中高收入的家庭75户,中等收入的家庭180户,低收入的家庭45户,为了了解生活购买力的某项指标,要从中抽取一个容量为50的样本
C.从1000名工人中,抽取100人调查上班途中所用的时间
D.从生产流水线上,抽取样本检查产品质量
练一练
B
例2.某公司有1000名员工,其中50名属于高收入者,150名属于中等收入者,800名属于低收入者.要对该公司员工的具体收入情况进行调查,欲抽取100名员工,应当怎样抽样比较合理?
同理,抽取15名中等收入者、80名低收入者,再对他们的具体收入状况分别进行调查.
解:采用分层随机抽样的方法.按照该公司员工的收入水平分成三层:高收入者、中等收入者、低收入者.
高收入者为50名,占所有员工的比例为 =5%,在所抽取的100名员工中,高收入者所占的比例也应为5%,即100×5%=5,所以应抽取5名高收入者比较合理.
分层抽样的操作步骤:
分层
将总体按一定的标准分层
定比
计算各层的个体数与总体的个体数的比
定量
按各层个体数与总体的个体数的比确定各层应抽取的样本容量
抽样
在每一层进行抽样
归纳总结
某学校有在编人员200人,其中行政人员20人,教师140人,后勤人员40人.教育部门为了解学校职工对学校县管校聘改革的意见,要从中抽取20人,试确定用何种方法抽样,并写出抽样过程.
练一练
解:(1)将200人分成行政人员、教师、后勤人员三层;
(2)按照的比例确定各层抽取的人数,行政人员:20×2(人),教师:140×14(人),后勤人员:40×4(人);
(3)在各层中用简单随机抽样的方法抽取样本;
(4)将抽取的20人综合到一起,即得到一个样本容量为20的样本.
方法类别 共同特点 抽样特征 相互联系 适应范围
简单随机抽样
分层抽样
抽样过程中每个个体被抽取的可能性相等
从总体中逐个不放回抽取
将总体分成互不交叉的几层,按比例分层抽样
各层抽样时采用简单随机抽样
总体中的个体数较少
总体由差异明显的几部分组成
两种抽样方法对比:
框图结构
分层随机抽样
操作步骤
概念
应用
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
