6.3.2 频率分布直方图 课件(共24张PPT)2023-2024学年高一数学北师大版(2019)必修一
文档属性
| 名称 | 6.3.2 频率分布直方图 课件(共24张PPT)2023-2024学年高一数学北师大版(2019)必修一 |

|
|
| 格式 | pptx | ||
| 文件大小 | 223.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 21:22:01 | ||
图片预览





文档简介
(共24张PPT)
6.3.2 频率分布直方图
新授课
1.能够对数据进行分析列频数分布表,画频率分布直方图、频率折线图.
2.会用样本的频率分布估计总体分布.
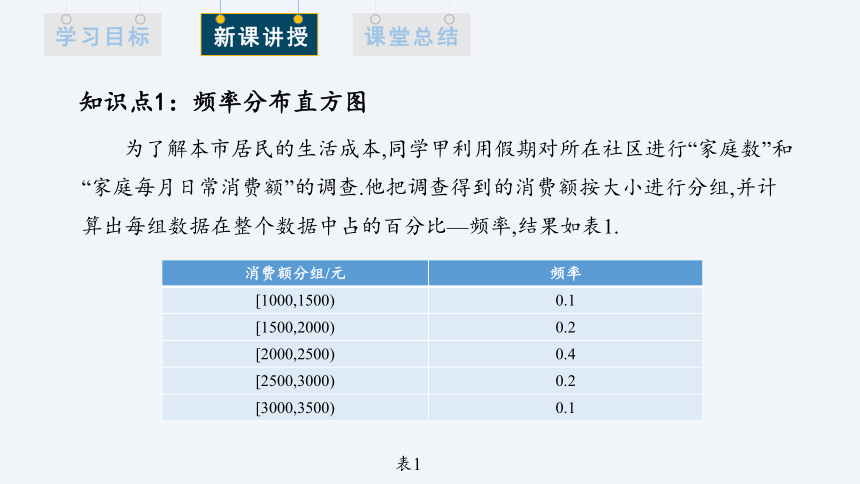
为了解本市居民的生活成本,同学甲利用假期对所在社区进行“家庭数”和“家庭每月日常消费额”的调查.他把调查得到的消费额按大小进行分组,并计算出每组数据在整个数据中占的百分比—频率,结果如表1.
消费额分组/元 频率
[1000,1500) 0.1
[1500,2000) 0.2
[2000,2500) 0.4
[2500,3000) 0.2
[3000,3500) 0.1
表1
知识点1:频率分布直方图
思考1:为了更直观的表示,整理数据通常采用图示的方法.我们学习过哪几种统计图?你认为哪种图更适合表示表1所示的数据?
消费额分组/元 频率
[1000,1500) 0.1
[1500,2000) 0.2
[2000,2500) 0.4
[2500,3000) 0.2
[3000,3500) 0.1
根据表1作出如下直方图:
问题:(1)小矩形的宽代表什么?高代表什么?面积代表什么?
(2)所有小矩形面积的总和是多少?
消费金额/元
O
0.0002
0.0004
0.0006
0.0008
1000
1500
2000
2500
3500
3000
图1
频率
组距
消费额分组/元 频率
[1000,1500) 0.1
[1500,2000) 0.2
[2000,2500) 0.4
[2500,3000) 0.2
[3000,3500) 0.1
表1
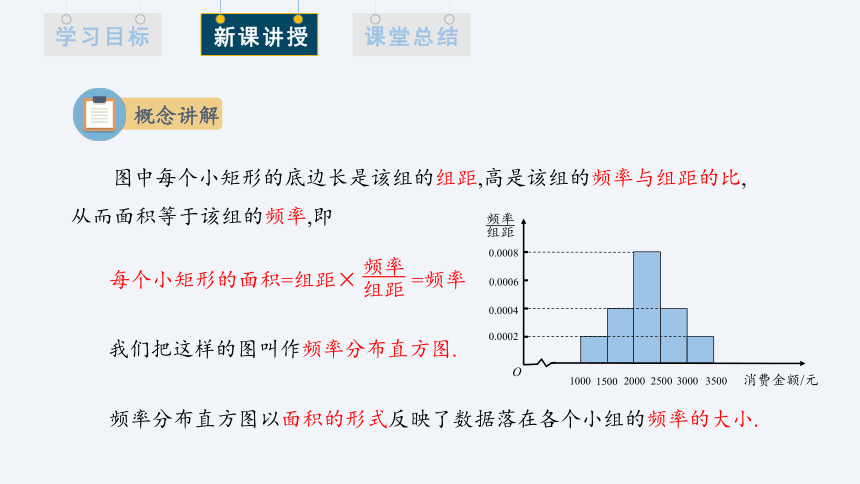
图中每个小矩形的底边长是该组的组距,高是该组的频率与组距的比,从而面积等于该组的频率,即
频率分布直方图以面积的形式反映了数据落在各个小组的频率的大小.
我们把这样的图叫作频率分布直方图.
频率
组距
每个小矩形的面积=组距× =频率
消费金额/元
O
0.0002
0.0004
0.0006
0.0008
1000
1500
2000
2500
3500
3000
频率
组距
概念讲解
(1) 能清楚直观地显示各组频率分布情况及各组频率之间的差别;
(2) 当考虑数据落在若干个组内的频率之和时,可以用相应矩形面积之和
来表示.
思考2:根据以上表格和图像的对比,频率分布直方图的优点有哪些?
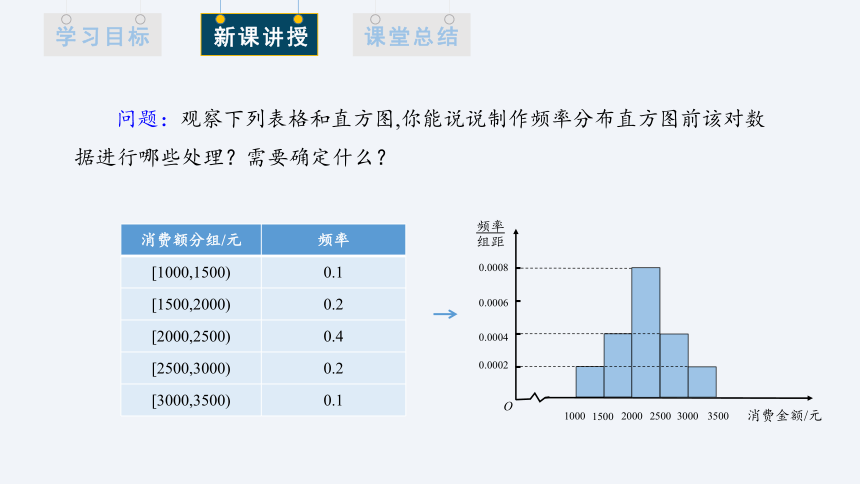
问题:观察下列表格和直方图,你能说说制作频率分布直方图前该对数据进行哪些处理?需要确定什么?
消费金额/元
O
0.0002
0.0004
0.0006
0.0008
1000
1500
2000
2500
3500
3000
频率
组距
消费额分组/元 频率
[1000,1500) 0.1
[1500,2000) 0.2
[2000,2500) 0.4
[2500,3000) 0.2
[3000,3500) 0.1
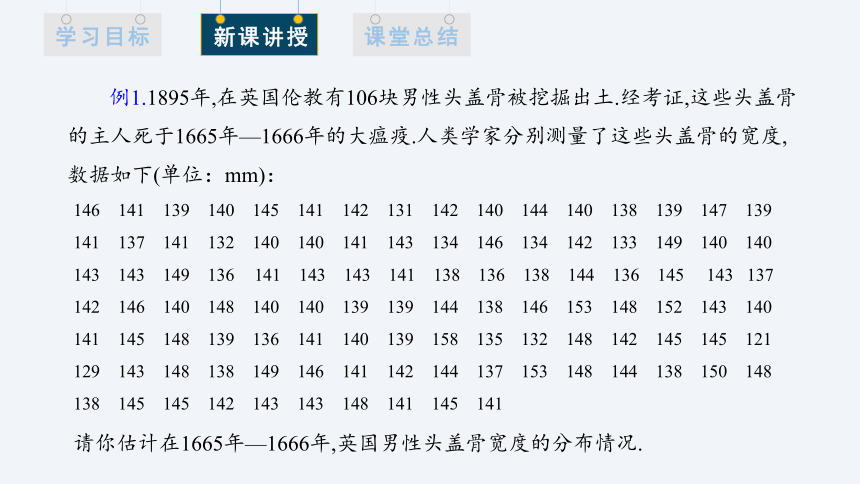
例1.1895年,在英国伦教有106块男性头盖骨被挖掘出土.经考证,这些头盖骨的主人死于1665年—1666年的大瘟疫.人类学家分别测量了这些头盖骨的宽度,数据如下(单位:mm):
146 141 139 140 145 141 142 131 142 140 144 140 138 139 147 139 141 137 141 132 140 140 141 143 134 146 134 142 133 149 140 140 143 143 149 136 141 143 143 141 138 136 138 144 136 145 143 137 142 146 140 148 140 140 139 139 144 138 146 153 148 152 143 140 141 145 148 139 136 141 140 139 158 135 132 148 142 145 145 121 129 143 148 138 149 146 141 142 144 137 153 148 144 138 150 148 138 145 145 142 143 143 148 141 145 141
请你估计在1665年—1666年,英国男性头盖骨宽度的分布情况.
宽度/mm 频数 频率
121 1 0.009
129 1 0.009
131 1 0.009
132 2 0.019
133 1 0.009
134 2 0.019
135 1 0.009
136 4 0.038
137 3 0.028
138 7 0.066
139 7 0.066
140 12 0.113
141 12 0.113
宽度/mm 频数 频率
142 7 0.066
143 10 0.094
144 5 0.047
145 8 0.075
146 5 0.047
147 1 0.009
148 8 0.075
149 3 0.028
150 1 0.009
152 1 0.009
153 2 0.019
158 1 0.009
频数分布表与频率分布表:
按照如下步骤处理数据:
(1)计算极差:158-121=37mm,这说明样本观测数据的变化范围是37mm.
(2)确定组距与组数:当数据在120个以内时,通常按照数据的多少分成5组~12组.一般要求各组的组距相等.取所有的组距为5mm,则 =7.4,即可以将数据分为8组.
(3)分组:由于组距为5mm,8个组距的总长度超过极差,因此可以使第一组的左端点略小于数据中的最小值,最后一组的右端点略大于数据中的最大值.所以本例中的106个数按如下方式分为8组:[120,125),[125,130),…,[155,160].
思考3:(1)分组时左(右)端点比实际数据小(大)ー点,对结论是否有影响
(2)所有区间都取左闭右开(最后一个取闭区间),这样做有什么好处?
宽度分组/mm 频数 频率 频率/组距
[120,125) 1 0.009 0.0018
[125,130) 1 0.009 0.0018
[130,135) 6 0.057 0.0114
[135,140) 22 0.208 0.0416
[140,145) 46 0.434 0.0868
[145,150) 25 0.236 0.0472
[150,155) 4 0.038 0.0076
[155,160) 1 0.009 0.0018
(4)列表:统计各组的信息(如表)
宽度/mm
120
125
130
140
150
160
135
145
155
0.0018
0.0018
0.0114
0.0416
0.0472
0.0868
0.0076
0.0018
0.02
0.04
0.06
0.08
0.10
O
频率
组距
(5)画频率分布直方图.
观察右图,回答下列问题:
(1)头盖骨的宽度位于哪个区间的频率最大?
[140,145)
43.4%
28.3%
(2)头盖骨的宽度在[140,145)的频率约是多少?
(3)头盖骨的宽度小于140mm的频率是多少
宽度/mm
120
125
130
140
150
160
135
145
155
0.0018
0.0018
0.0114
0.0416
0.0472
0.0868
0.0076
0.0018
0.02
0.04
0.06
0.08
0.10
O
频率
组距
归纳总结
画频率分布直方图的步骤:
①求极差
②确定组距与组数
③将数据分组
④列频率分布表
⑤画频率分布直方图
思考4:前面我们学均数、众数、中位数,在频率分布直方图中,这些数据是怎样体现的?
平均值的估计值等于每个小矩形的面积乘小矩形底边中点的横坐标之和;
中位数的估计值,应使其左右两边的直方图面积相等;
最高小矩形的中点所对应的数据值即为这组数据的众数.
宽度/mm
120
125
130
140
150
160
135
145
155
0.0018
0.0018
0.0114
0.0416
0.0472
0.0868
0.0076
0.0018
0.02
0.04
0.06
0.08
0.10
O
频率
组距
思考5:请你根据以上数据,以10为组距画出频率分布直方图.该过程中频率分布表中的数字和频率分布直方图的形状有变化吗?如果是变化的,这个变化与什么有关?当样本容量逐渐增大时,直方图的分布有无规律可循?
(1)频率分布表中的数字和频率分布直方图的形状都与分组数有关,频率分布直方图的形状还与平面直角坐标系的单位长度选取有关.
(2)频率分布表与频率分布直方图由样本决定,它们随着样本的改变而改变.
(3)尽管有上述变化,但是频率分布是有规律的,若固定分组数,随着样本容量的增加,频率分布表中的各个频率会稳定在相应分组的某个数值上.
注意:(1)画折线图时,在频率分布直方图的左右两边各加一个区间;
(2)从所加的左边区间的中点起,用线段连接各矩形的顶端中点,直至右边所加的中点.
0.02
0.04
0.06
0.08
0.10
O
频率
组距
宽度/mm
0.0018
0.0018
0.0114
0.0416
0.0472
0.0868
0.0076
0.0018
120
125
130
140
150
160
135
145
155
115
165
绘制频率折线图
知识点2:频率折线图
思考6:频率折线图能否大致反映总体的情况?如果不断增大样本容量,分组数也随之增多,频率折线图会有怎么样的变化?
能.如果不断增大样本容量,分组间距不断缩小,折线图会越来越接近于一条光滑曲线.
当样本量不断增大时,样本中落在每个区间内的个体的频率会越来越稳定于总体在相应区间内取值的比例.
因此,我们就可以用样本的频率分布去估计总体在相应区间内取值的比例,也就得到了总体的分布情况.样本容量越大,估计越准确.
归纳总结
1.容量为20的样本数据,分组后的频数如表:
练一练
分组 [10,20) [20,30) [30,40) [40,50) [50,60) [60,70)
频数 2 3 4 5 4 2
则样本数据落在区间[10,40)的频率为____.
0.45
2.为了研究某药品的疗效,选取若干名志愿者进行临床试验.所有志愿者的舒张压数据(单位:kPa)的分组区间分别为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组…第五组.如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为____.
12
舒张压/kPa
O
0.08
0.16
0.24
0.36
12
13
14
15
17
16
频率
组距
3.某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了
150分~450分的1000名学生的成绩,并根据这1000名学生的成绩画出样本的频
率分布直方图(如图).本地区参加模拟考试的学生一共有30000名,则估计该地
区模拟考试成绩在[300,350)内的学生共有_____名
9000
成绩/分
O
0.001
0.004
0.005
0.006
150
200
250
300
400
350
频率
组距
0.003
450
频率折线图
频率分布直方图
频率分布表
用样本估计
总体分布
应用
框图结构
6.3.2 频率分布直方图
新授课
1.能够对数据进行分析列频数分布表,画频率分布直方图、频率折线图.
2.会用样本的频率分布估计总体分布.
为了解本市居民的生活成本,同学甲利用假期对所在社区进行“家庭数”和“家庭每月日常消费额”的调查.他把调查得到的消费额按大小进行分组,并计算出每组数据在整个数据中占的百分比—频率,结果如表1.
消费额分组/元 频率
[1000,1500) 0.1
[1500,2000) 0.2
[2000,2500) 0.4
[2500,3000) 0.2
[3000,3500) 0.1
表1
知识点1:频率分布直方图
思考1:为了更直观的表示,整理数据通常采用图示的方法.我们学习过哪几种统计图?你认为哪种图更适合表示表1所示的数据?
消费额分组/元 频率
[1000,1500) 0.1
[1500,2000) 0.2
[2000,2500) 0.4
[2500,3000) 0.2
[3000,3500) 0.1
根据表1作出如下直方图:
问题:(1)小矩形的宽代表什么?高代表什么?面积代表什么?
(2)所有小矩形面积的总和是多少?
消费金额/元
O
0.0002
0.0004
0.0006
0.0008
1000
1500
2000
2500
3500
3000
图1
频率
组距
消费额分组/元 频率
[1000,1500) 0.1
[1500,2000) 0.2
[2000,2500) 0.4
[2500,3000) 0.2
[3000,3500) 0.1
表1
图中每个小矩形的底边长是该组的组距,高是该组的频率与组距的比,从而面积等于该组的频率,即
频率分布直方图以面积的形式反映了数据落在各个小组的频率的大小.
我们把这样的图叫作频率分布直方图.
频率
组距
每个小矩形的面积=组距× =频率
消费金额/元
O
0.0002
0.0004
0.0006
0.0008
1000
1500
2000
2500
3500
3000
频率
组距
概念讲解
(1) 能清楚直观地显示各组频率分布情况及各组频率之间的差别;
(2) 当考虑数据落在若干个组内的频率之和时,可以用相应矩形面积之和
来表示.
思考2:根据以上表格和图像的对比,频率分布直方图的优点有哪些?
问题:观察下列表格和直方图,你能说说制作频率分布直方图前该对数据进行哪些处理?需要确定什么?
消费金额/元
O
0.0002
0.0004
0.0006
0.0008
1000
1500
2000
2500
3500
3000
频率
组距
消费额分组/元 频率
[1000,1500) 0.1
[1500,2000) 0.2
[2000,2500) 0.4
[2500,3000) 0.2
[3000,3500) 0.1
例1.1895年,在英国伦教有106块男性头盖骨被挖掘出土.经考证,这些头盖骨的主人死于1665年—1666年的大瘟疫.人类学家分别测量了这些头盖骨的宽度,数据如下(单位:mm):
146 141 139 140 145 141 142 131 142 140 144 140 138 139 147 139 141 137 141 132 140 140 141 143 134 146 134 142 133 149 140 140 143 143 149 136 141 143 143 141 138 136 138 144 136 145 143 137 142 146 140 148 140 140 139 139 144 138 146 153 148 152 143 140 141 145 148 139 136 141 140 139 158 135 132 148 142 145 145 121 129 143 148 138 149 146 141 142 144 137 153 148 144 138 150 148 138 145 145 142 143 143 148 141 145 141
请你估计在1665年—1666年,英国男性头盖骨宽度的分布情况.
宽度/mm 频数 频率
121 1 0.009
129 1 0.009
131 1 0.009
132 2 0.019
133 1 0.009
134 2 0.019
135 1 0.009
136 4 0.038
137 3 0.028
138 7 0.066
139 7 0.066
140 12 0.113
141 12 0.113
宽度/mm 频数 频率
142 7 0.066
143 10 0.094
144 5 0.047
145 8 0.075
146 5 0.047
147 1 0.009
148 8 0.075
149 3 0.028
150 1 0.009
152 1 0.009
153 2 0.019
158 1 0.009
频数分布表与频率分布表:
按照如下步骤处理数据:
(1)计算极差:158-121=37mm,这说明样本观测数据的变化范围是37mm.
(2)确定组距与组数:当数据在120个以内时,通常按照数据的多少分成5组~12组.一般要求各组的组距相等.取所有的组距为5mm,则 =7.4,即可以将数据分为8组.
(3)分组:由于组距为5mm,8个组距的总长度超过极差,因此可以使第一组的左端点略小于数据中的最小值,最后一组的右端点略大于数据中的最大值.所以本例中的106个数按如下方式分为8组:[120,125),[125,130),…,[155,160].
思考3:(1)分组时左(右)端点比实际数据小(大)ー点,对结论是否有影响
(2)所有区间都取左闭右开(最后一个取闭区间),这样做有什么好处?
宽度分组/mm 频数 频率 频率/组距
[120,125) 1 0.009 0.0018
[125,130) 1 0.009 0.0018
[130,135) 6 0.057 0.0114
[135,140) 22 0.208 0.0416
[140,145) 46 0.434 0.0868
[145,150) 25 0.236 0.0472
[150,155) 4 0.038 0.0076
[155,160) 1 0.009 0.0018
(4)列表:统计各组的信息(如表)
宽度/mm
120
125
130
140
150
160
135
145
155
0.0018
0.0018
0.0114
0.0416
0.0472
0.0868
0.0076
0.0018
0.02
0.04
0.06
0.08
0.10
O
频率
组距
(5)画频率分布直方图.
观察右图,回答下列问题:
(1)头盖骨的宽度位于哪个区间的频率最大?
[140,145)
43.4%
28.3%
(2)头盖骨的宽度在[140,145)的频率约是多少?
(3)头盖骨的宽度小于140mm的频率是多少
宽度/mm
120
125
130
140
150
160
135
145
155
0.0018
0.0018
0.0114
0.0416
0.0472
0.0868
0.0076
0.0018
0.02
0.04
0.06
0.08
0.10
O
频率
组距
归纳总结
画频率分布直方图的步骤:
①求极差
②确定组距与组数
③将数据分组
④列频率分布表
⑤画频率分布直方图
思考4:前面我们学均数、众数、中位数,在频率分布直方图中,这些数据是怎样体现的?
平均值的估计值等于每个小矩形的面积乘小矩形底边中点的横坐标之和;
中位数的估计值,应使其左右两边的直方图面积相等;
最高小矩形的中点所对应的数据值即为这组数据的众数.
宽度/mm
120
125
130
140
150
160
135
145
155
0.0018
0.0018
0.0114
0.0416
0.0472
0.0868
0.0076
0.0018
0.02
0.04
0.06
0.08
0.10
O
频率
组距
思考5:请你根据以上数据,以10为组距画出频率分布直方图.该过程中频率分布表中的数字和频率分布直方图的形状有变化吗?如果是变化的,这个变化与什么有关?当样本容量逐渐增大时,直方图的分布有无规律可循?
(1)频率分布表中的数字和频率分布直方图的形状都与分组数有关,频率分布直方图的形状还与平面直角坐标系的单位长度选取有关.
(2)频率分布表与频率分布直方图由样本决定,它们随着样本的改变而改变.
(3)尽管有上述变化,但是频率分布是有规律的,若固定分组数,随着样本容量的增加,频率分布表中的各个频率会稳定在相应分组的某个数值上.
注意:(1)画折线图时,在频率分布直方图的左右两边各加一个区间;
(2)从所加的左边区间的中点起,用线段连接各矩形的顶端中点,直至右边所加的中点.
0.02
0.04
0.06
0.08
0.10
O
频率
组距
宽度/mm
0.0018
0.0018
0.0114
0.0416
0.0472
0.0868
0.0076
0.0018
120
125
130
140
150
160
135
145
155
115
165
绘制频率折线图
知识点2:频率折线图
思考6:频率折线图能否大致反映总体的情况?如果不断增大样本容量,分组数也随之增多,频率折线图会有怎么样的变化?
能.如果不断增大样本容量,分组间距不断缩小,折线图会越来越接近于一条光滑曲线.
当样本量不断增大时,样本中落在每个区间内的个体的频率会越来越稳定于总体在相应区间内取值的比例.
因此,我们就可以用样本的频率分布去估计总体在相应区间内取值的比例,也就得到了总体的分布情况.样本容量越大,估计越准确.
归纳总结
1.容量为20的样本数据,分组后的频数如表:
练一练
分组 [10,20) [20,30) [30,40) [40,50) [50,60) [60,70)
频数 2 3 4 5 4 2
则样本数据落在区间[10,40)的频率为____.
0.45
2.为了研究某药品的疗效,选取若干名志愿者进行临床试验.所有志愿者的舒张压数据(单位:kPa)的分组区间分别为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组…第五组.如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为____.
12
舒张压/kPa
O
0.08
0.16
0.24
0.36
12
13
14
15
17
16
频率
组距
3.某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了
150分~450分的1000名学生的成绩,并根据这1000名学生的成绩画出样本的频
率分布直方图(如图).本地区参加模拟考试的学生一共有30000名,则估计该地
区模拟考试成绩在[300,350)内的学生共有_____名
9000
成绩/分
O
0.001
0.004
0.005
0.006
150
200
250
300
400
350
频率
组距
0.003
450
频率折线图
频率分布直方图
频率分布表
用样本估计
总体分布
应用
框图结构
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
