7.3 频率与概率 课件(共18张PPT)2023-2024学年高一数学北师大版(2019)必修一
文档属性
| 名称 | 7.3 频率与概率 课件(共18张PPT)2023-2024学年高一数学北师大版(2019)必修一 |

|
|
| 格式 | pptx | ||
| 文件大小 | 662.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 21:17:58 | ||
图片预览





文档简介
(共18张PPT)
7.3 频率与概率
新授课
1.通过试验和历史数据体会频率的随机性与规律性.
2.理解频率的统计定义,理解频率与概率的关系.
回顾:投掷一枚均匀的骰子,掷出的点数为偶数的概率是多少
若投掷一枚不均匀的骰子,掷出点数为偶数的概率又是多少呢
频率
概率
问题1:(1)对于任何一位篮球运动员,在一次投篮中,命中与否是一个随机事件.球迷说某某球员投篮很准,这个“很准”是怎么得来的?是否有一个量化的标准?
(2)在篮球比赛决定胜负的一投时,往往会将这决定胜负的一投交给“最有把握”的球员.这里的“最有把握”是怎么得来的呢?
技术指标:篮球命中率.
篮球命中率越大,说明其投篮越准,越有把握.
“投篮命中率”往往用一个比值 表示,其中n表示投篮的总次数,m表示在这n次投篮命中的次数.
知识点1:频率的随机性和规律性
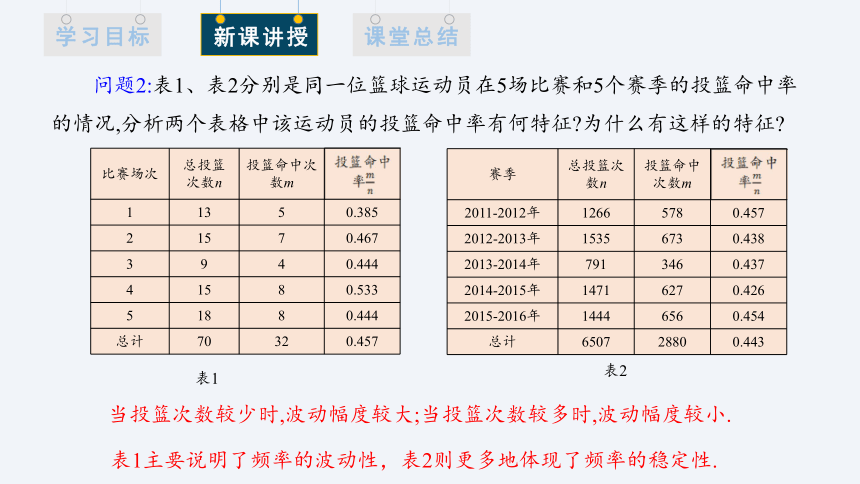
问题2:表1、表2分别是同一位篮球运动员在5场比赛和5个赛季的投篮命中率的情况,分析两个表格中该运动员的投篮命中率有何特征 为什么有这样的特征
比赛场次 总投篮次数n 投篮命中次数m 投篮命中率
1 13 5 0.385
2 15 7 0.467
3 9 4 0.444
4 15 8 0.533
5 18 8 0.444
总计 70 32 0.457
表1
赛季 总投篮次数n 投篮命中次数m 投篮命中率
2011-2012年 1266 578 0.457
2012-2013年 1535 673 0.438
2013-2014年 791 346 0.437
2014-2015年 1471 627 0.426
2015-2016年 1444 656 0.454
总计 6507 2880 0.443
表2
当投篮次数较少时,波动幅度较大;当投篮次数较多时,波动幅度较小.
表1主要说明了频率的波动性,表2则更多地体现了频率的稳定性.
方法一:动手操作.
第1步:每个同学取一枚硬币,做20次抛掷硬币试验,记录“正面向上”的次数,并计算出“正面向上”的比例,填在下表中.
问题3:由古典概型我们知道,抛掷一枚均匀的硬币,正面朝上的概率是,因此,抛掷一枚均匀的硬币10次,正面朝上的次数一定是5次吗?如果不是5次,是不是意味着这枚硬币不均匀呢?如何验证这枚硬币是否均匀呢?
姓名 试验次数n 正面向上的次数m 正面向上的比例
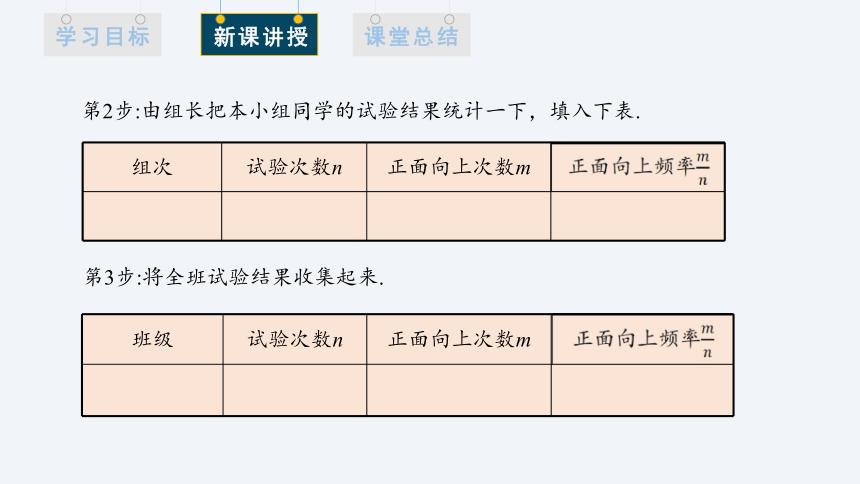
第2步:由组长把本小组同学的试验结果统计一下,填入下表.
组次 试验次数n 正面向上次数m 正面向上频率
第3步:将全班试验结果收集起来.
班级 试验次数n 正面向上次数m 正面向上频率
方法二:随机模拟
试验者 总抛掷次数n 正面朝上的次数m 正面朝上的频率
德·摩根
布丰
费勒
皮尔逊
罗曼诺夫斯基
材料1:历史上曾有很多人做过抛掷硬币试验,其结果如表3(结果精确到0.0001).
表3
抛掷次数逐渐增大,正面朝上的频率稳定在0.5左右
4092 2048 0.5005
4040 2048 0.5069
10000 4979 0.4979
24000 12012 0.5005
80640 39699 0.4923
出生年份 出生总人数 男孩数 频率
1927 958733 496544
1928 990933 513654
1929 994101 514765
1930 1022811 528072
1931 964573 496986
1932 934663 482431
总计 5865814 3032452
材料2:表4是20世纪波兰的新生儿数及其中男婴数的统计资料(结果精确到0.001).
0.518
0.518
0.518
0.516
0.515
0.516
0.517
著名数学家拉普拉斯研究显示男孩出生的频率在附近摆动,上述统计资料符合这个结果吗
表4
思考:随着试验次数的不断增加,投篮命中率、硬币正面朝上、新生儿中男婴的频率变化有何共同特征
频率通常会在某个常数附近摆动
在相同条件下,大量重复进行同一试验时,随机事件A发生的频率通常会在某个常数附近摆动,即随机事件A发生的频率具有稳定性.
这个常数叫作随机事件A的概率,记作P(A)(0≤P(A)≤1).
通常用频率来估计概率.
概念生成
思考:1.随机事件A发生的概率P(A)是一个常数,这个常数是用来度量什么的?有何意义?
2.随机事件A发生的概率与A发生的频率有什么区别和联系?
知识点2:频率与概率的关系
(1)频率是概率的近似值,随着试验次数的增加,频率通常会稳定在概率附近.在实际问题中,通常随机事件的概率是未知的,常用频率作为概率的估计值.
(2)频率是随机的,在试验前是不能确定的;
(3)概率是一个确定的数,是客观存在的,是频率在理论上的期望值,与每次试验无关,与试验的次数无关.
频率和概率的关系:
归纳总结
问题4:(1)天气预报:“明天降雨的概率是80%”,明天出门是否一定下雨
(2)某彩票中奖的概率为1%,你买100张彩票是否一定中奖
(3)抛掷一枚均匀的硬币,出现正面的概率为0.5,那么连续抛掷这枚硬币2次,一定出现一次正面、一次反面吗
不一定
不一定
不一定
在一次或若干次试验中,随机事件发生与否具有偶然性,但是随着试验次数的增加,即可排除偶然性因素影响,显露出事物的本质.
练一练
某射手在同一条件下进行射击,结果如下:
射击次数n 10 30 50 100 200 500
击中靶心的次数m 9 28 44 92 178 455
击中靶心的频率
0.90
0.93
0.88
0.92
0.89
0.91
(1)计算表中击中靶心的各个频率(精确到0.01);
(2)这个射手射击一次,击中靶心的概率约为多少?
0.90
根据今天所学,回答下列问题:
(1)频率和概率有何区别和联系 这种关系反映了随机现象的什么特点
(2)本节课所学概率与古典概型中的概率有何区别和联系
7.3 频率与概率
新授课
1.通过试验和历史数据体会频率的随机性与规律性.
2.理解频率的统计定义,理解频率与概率的关系.
回顾:投掷一枚均匀的骰子,掷出的点数为偶数的概率是多少
若投掷一枚不均匀的骰子,掷出点数为偶数的概率又是多少呢
频率
概率
问题1:(1)对于任何一位篮球运动员,在一次投篮中,命中与否是一个随机事件.球迷说某某球员投篮很准,这个“很准”是怎么得来的?是否有一个量化的标准?
(2)在篮球比赛决定胜负的一投时,往往会将这决定胜负的一投交给“最有把握”的球员.这里的“最有把握”是怎么得来的呢?
技术指标:篮球命中率.
篮球命中率越大,说明其投篮越准,越有把握.
“投篮命中率”往往用一个比值 表示,其中n表示投篮的总次数,m表示在这n次投篮命中的次数.
知识点1:频率的随机性和规律性
问题2:表1、表2分别是同一位篮球运动员在5场比赛和5个赛季的投篮命中率的情况,分析两个表格中该运动员的投篮命中率有何特征 为什么有这样的特征
比赛场次 总投篮次数n 投篮命中次数m 投篮命中率
1 13 5 0.385
2 15 7 0.467
3 9 4 0.444
4 15 8 0.533
5 18 8 0.444
总计 70 32 0.457
表1
赛季 总投篮次数n 投篮命中次数m 投篮命中率
2011-2012年 1266 578 0.457
2012-2013年 1535 673 0.438
2013-2014年 791 346 0.437
2014-2015年 1471 627 0.426
2015-2016年 1444 656 0.454
总计 6507 2880 0.443
表2
当投篮次数较少时,波动幅度较大;当投篮次数较多时,波动幅度较小.
表1主要说明了频率的波动性,表2则更多地体现了频率的稳定性.
方法一:动手操作.
第1步:每个同学取一枚硬币,做20次抛掷硬币试验,记录“正面向上”的次数,并计算出“正面向上”的比例,填在下表中.
问题3:由古典概型我们知道,抛掷一枚均匀的硬币,正面朝上的概率是,因此,抛掷一枚均匀的硬币10次,正面朝上的次数一定是5次吗?如果不是5次,是不是意味着这枚硬币不均匀呢?如何验证这枚硬币是否均匀呢?
姓名 试验次数n 正面向上的次数m 正面向上的比例
第2步:由组长把本小组同学的试验结果统计一下,填入下表.
组次 试验次数n 正面向上次数m 正面向上频率
第3步:将全班试验结果收集起来.
班级 试验次数n 正面向上次数m 正面向上频率
方法二:随机模拟
试验者 总抛掷次数n 正面朝上的次数m 正面朝上的频率
德·摩根
布丰
费勒
皮尔逊
罗曼诺夫斯基
材料1:历史上曾有很多人做过抛掷硬币试验,其结果如表3(结果精确到0.0001).
表3
抛掷次数逐渐增大,正面朝上的频率稳定在0.5左右
4092 2048 0.5005
4040 2048 0.5069
10000 4979 0.4979
24000 12012 0.5005
80640 39699 0.4923
出生年份 出生总人数 男孩数 频率
1927 958733 496544
1928 990933 513654
1929 994101 514765
1930 1022811 528072
1931 964573 496986
1932 934663 482431
总计 5865814 3032452
材料2:表4是20世纪波兰的新生儿数及其中男婴数的统计资料(结果精确到0.001).
0.518
0.518
0.518
0.516
0.515
0.516
0.517
著名数学家拉普拉斯研究显示男孩出生的频率在附近摆动,上述统计资料符合这个结果吗
表4
思考:随着试验次数的不断增加,投篮命中率、硬币正面朝上、新生儿中男婴的频率变化有何共同特征
频率通常会在某个常数附近摆动
在相同条件下,大量重复进行同一试验时,随机事件A发生的频率通常会在某个常数附近摆动,即随机事件A发生的频率具有稳定性.
这个常数叫作随机事件A的概率,记作P(A)(0≤P(A)≤1).
通常用频率来估计概率.
概念生成
思考:1.随机事件A发生的概率P(A)是一个常数,这个常数是用来度量什么的?有何意义?
2.随机事件A发生的概率与A发生的频率有什么区别和联系?
知识点2:频率与概率的关系
(1)频率是概率的近似值,随着试验次数的增加,频率通常会稳定在概率附近.在实际问题中,通常随机事件的概率是未知的,常用频率作为概率的估计值.
(2)频率是随机的,在试验前是不能确定的;
(3)概率是一个确定的数,是客观存在的,是频率在理论上的期望值,与每次试验无关,与试验的次数无关.
频率和概率的关系:
归纳总结
问题4:(1)天气预报:“明天降雨的概率是80%”,明天出门是否一定下雨
(2)某彩票中奖的概率为1%,你买100张彩票是否一定中奖
(3)抛掷一枚均匀的硬币,出现正面的概率为0.5,那么连续抛掷这枚硬币2次,一定出现一次正面、一次反面吗
不一定
不一定
不一定
在一次或若干次试验中,随机事件发生与否具有偶然性,但是随着试验次数的增加,即可排除偶然性因素影响,显露出事物的本质.
练一练
某射手在同一条件下进行射击,结果如下:
射击次数n 10 30 50 100 200 500
击中靶心的次数m 9 28 44 92 178 455
击中靶心的频率
0.90
0.93
0.88
0.92
0.89
0.91
(1)计算表中击中靶心的各个频率(精确到0.01);
(2)这个射手射击一次,击中靶心的概率约为多少?
0.90
根据今天所学,回答下列问题:
(1)频率和概率有何区别和联系 这种关系反映了随机现象的什么特点
(2)本节课所学概率与古典概型中的概率有何区别和联系
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
