2023-2024学年数学八年级平行四边形单元测试试题(人教版(五四制))基础卷含解析
文档属性
| 名称 | 2023-2024学年数学八年级平行四边形单元测试试题(人教版(五四制))基础卷含解析 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-21 18:10:36 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学七年级平行四边形(人教版(五四制))单元测试 基础卷 含解析
学校:___________姓名:___________班级:___________考号:___________
一、单选题(共30分)
1.(本题3分)如图,在中,,,,则的面积为( )
A.30 B.60 C.65 D.
2.(本题3分)如图,有两条相互垂直的卡槽,一小哥将一根木棒的两端分别卡在卡槽中,在木棒的中部插有一支记号笔,接着移动木棒的一端,另一端也随之移动.我们惊讶地发现:记号笔画出了一段圆弧!根据你所学的有关直角三角形的知识,分析“木棒作弧”中所运用的数学道理是( )
A.直角三角形的两直角边长度的平方和等于第三边长度的平方
B.直角三角形的面积等于两直角边乘积的一半
C.直角三角形的两个锐角互余
D.直角三角形斜边上的中线等于斜边的一半
3.(本题3分)如图,在四边形中,,,点E为的中点,连结,若四边形的面积为16,则的面积为( )
A.2 B.4 C.8 D.16
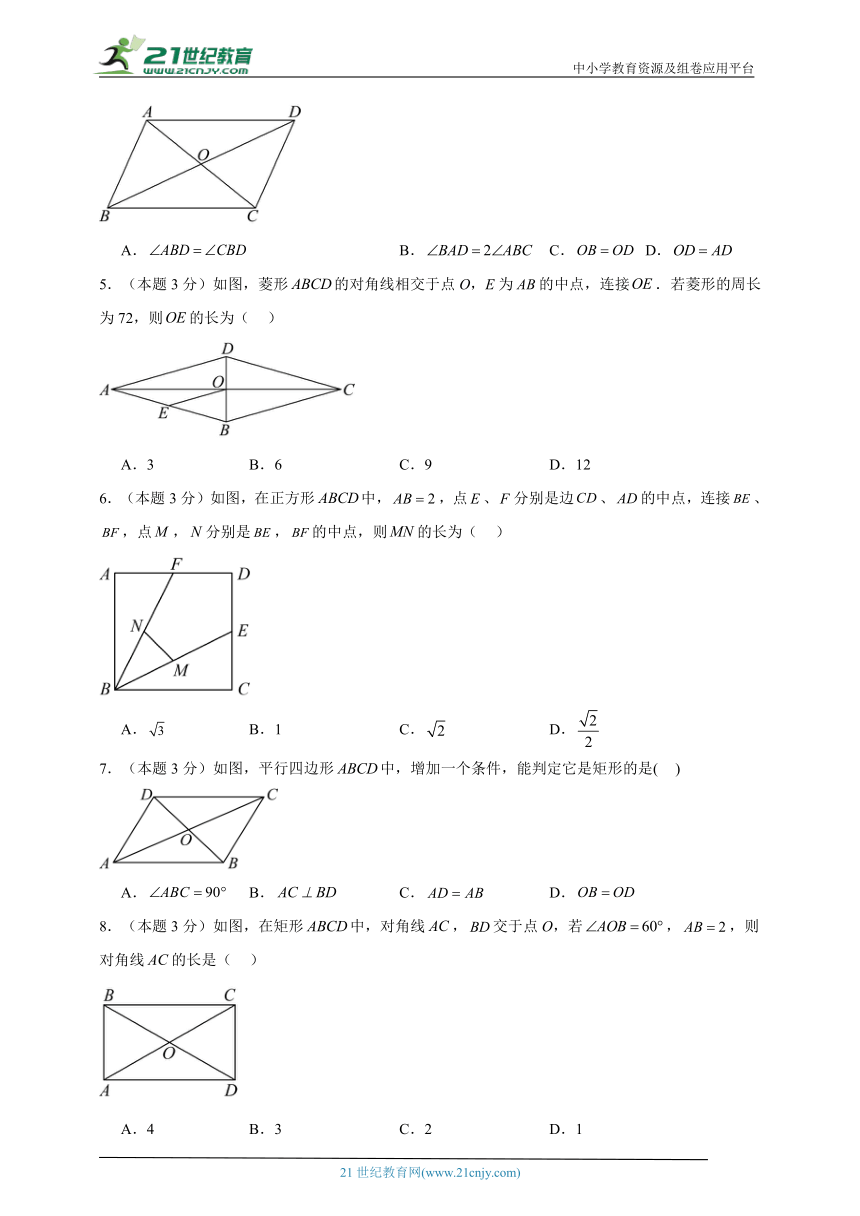
4.(本题3分)如图,平行四边形的对角线相交于点O,下列说法正确的是( )
A. B. C. D.
5.(本题3分)如图,菱形的对角线相交于点O,E为的中点,连接.若菱形的周长为72,则的长为( )
A.3 B.6 C.9 D.12
6.(本题3分)如图,在正方形中,,点、分别是边、的中点,连接、,点,分别是,的中点,则的长为( )
A. B.1 C. D.
7.(本题3分)如图,平行四边形中,增加一个条件,能判定它是矩形的是( )
A. B. C. D.
8.(本题3分)如图,在矩形中,对角线,交于点O,若,,则对角线的长是( )
A.4 B.3 C.2 D.1
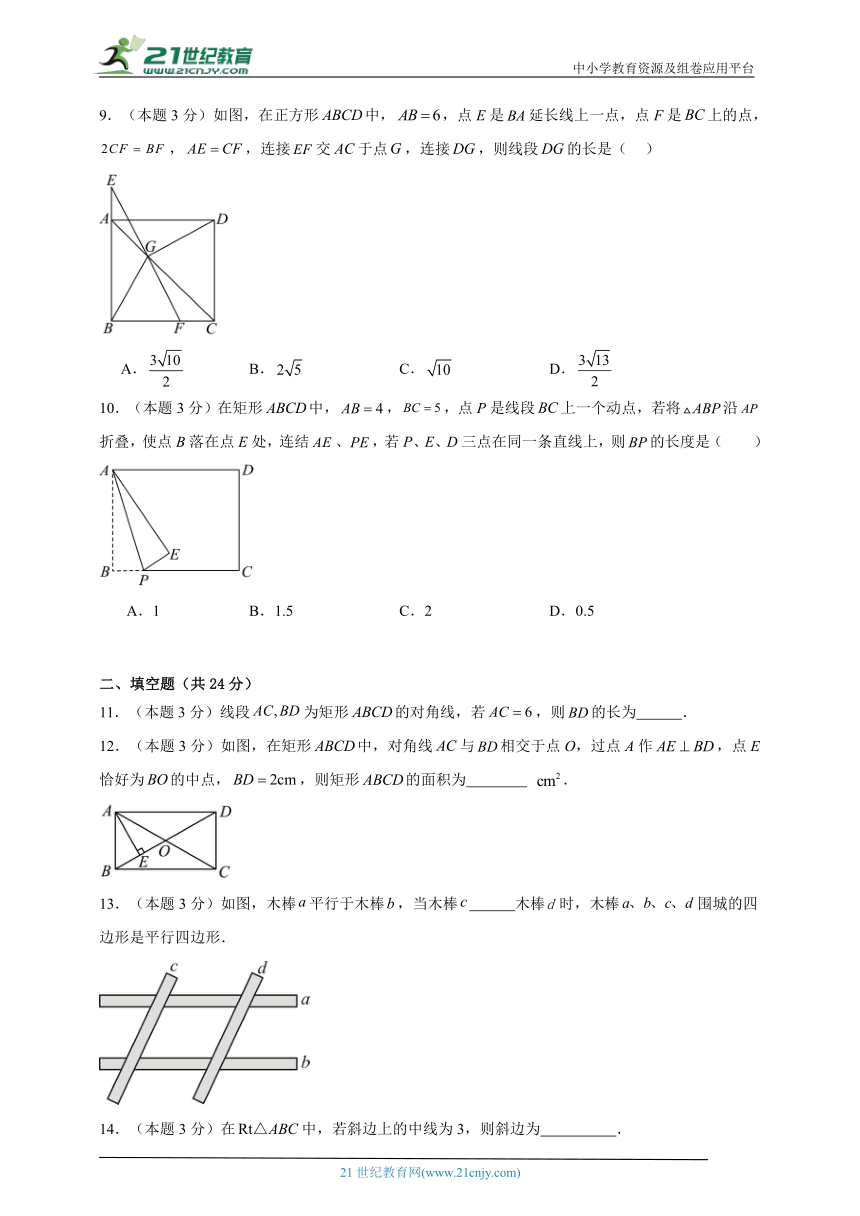
9.(本题3分)如图,在正方形中,,点E是延长线上一点,点F是上的点,,,连接交于点,连接,则线段的长是( )
A. B. C. D.
10.(本题3分)在矩形中,,,点P是线段上一个动点,若将沿折叠,使点B落在点E处,连结、,若P、E、D三点在同一条直线上,则的长度是( )
A.1 B.1.5 C.2 D.0.5
二、填空题(共24分)
11.(本题3分)线段为矩形的对角线,若,则的长为 .
12.(本题3分)如图,在矩形中,对角线与相交于点O,过点A作,点E恰好为的中点,,则矩形的面积为 .
13.(本题3分)如图,木棒平行于木棒,当木棒 木棒时,木棒围城的四边形是平行四边形.
14.(本题3分)在中,若斜边上的中线为3,则斜边为 .
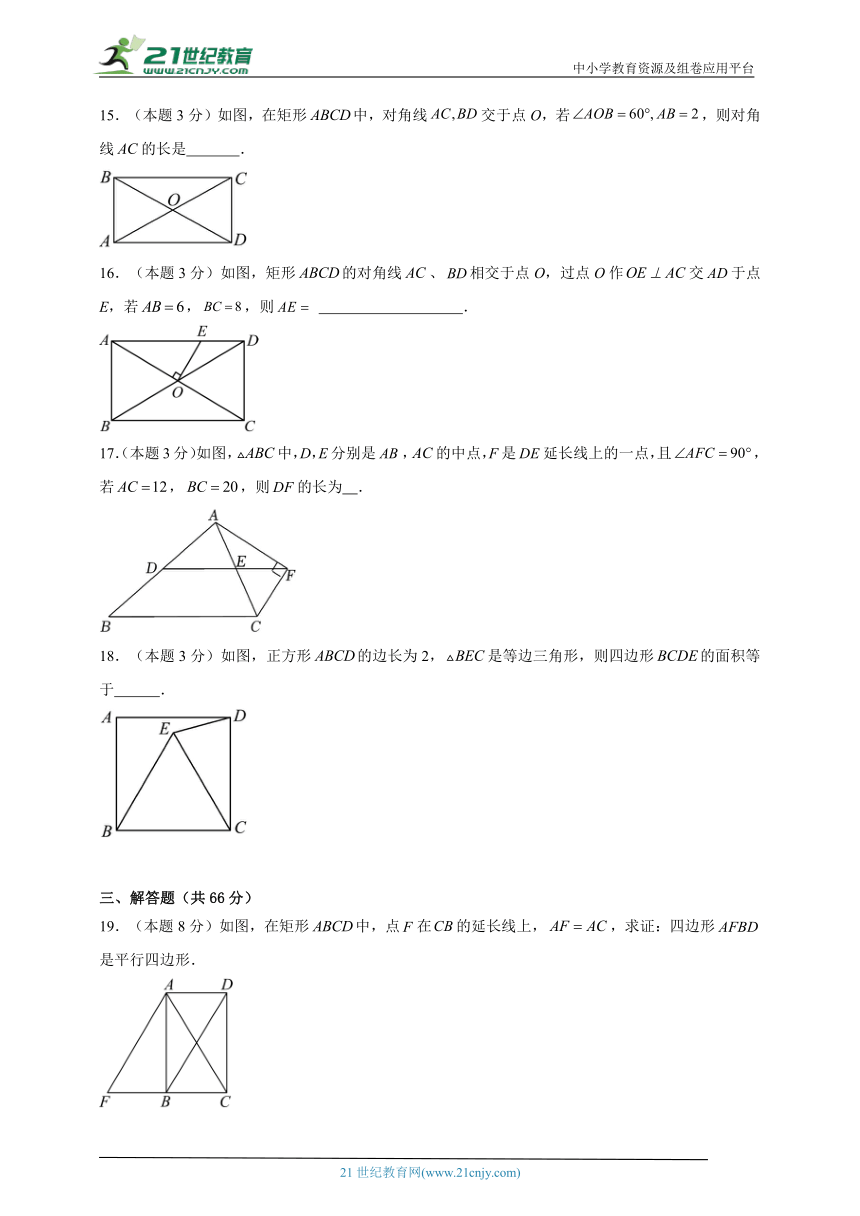
15.(本题3分)如图,在矩形中,对角线交于点O,若,则对角线的长是 .
16.(本题3分)如图,矩形的对角线、相交于点O,过点O作交于点E,若,,则 .
17.(本题3分)如图,中,D,E分别是,的中点,F是延长线上的一点,且,若,,则的长为 .
18.(本题3分)如图,正方形的边长为2,是等边三角形,则四边形的面积等于 .
三、解答题(共66分)
19.(本题8分)如图,在矩形中,点在的延长线上,,求证:四边形是平行四边形.
20.(本题8分)如图,在平行四边形中,连接对角线,过点作于点.
(1)用尺规完成以下基本作图:过点作的垂线,垂足为.(保留作图痕迹,不写作法)
(2)在(1)问所作的图形中,连接,求证:四边形是平行四边形.
证明:
∵四边形是平行四边形,
∴ ,.
∴ .
.
.
∴ .
在和中:
.
∴ .
,.
∴四边形是平行四边形.
21.(本题10分)已知点,分别是平行四边形的边,的中点.求证:.
22.(本题10分)如图,在平行四边形中,的平分线交于点E,的平分线交于点F.求证:.
23.(本题10分)如图,的对角线,相交于点,过点且与,分别相交于点,.求证:.
24.(本题10分)如图,过菱形的顶点A作于点E,延长至点F,使,连接.
(1)求证:四边形是矩形;
(2)若,求的长.
25.(本题10分)如图,四边形的对角线,相交于点,,为矩形对角线,.
(1)求证:四边形是菱形;
(2)连接,若,的值.
参考答案:
1.B
【分析】
本题考查的是勾股定理的应用,平行四边形的性质,先证明,再利用勾股定理求解,再利用面积公式进行计算即可.
【详解】
解:∵四边形为平行四边形,
∴.
∵,
∴是直角三角形,
∴,
∴.
故选B.
2.D
【分析】
本题考查了直角三角形的性质,熟记“直角三角形斜边上的中线等于斜边的一半”是解题关键.
【详解】解:因为“木棒作弧”过程中弧上的点到两条相互垂直的卡槽交点距离相等,且木棒作为三角形的斜边,记号笔在木棒的中点,
所以运用了直角三角形斜边上的中线等于斜边的一半,
故选:D.
3.B
【分析】
本题考查的是三角形的中线的性质,平行四边形的判定与性质,先证明四边形是平行四边形,再利用平行四边形的性质与三角形的中线等分三角形的面积可得答案.
【详解】解:∵,,
∴四边形是平行四边形,
∵四边形的面积为16,
∴,
∵点E为的中点,
∴,
故选B
4.C
【分析】本题考查了平行四边形的性质,由平行四边形的性质可得,即可求解,掌握平行四边形的性质是解题的关键.
【详解】∵四边形是平行四边形,
∴,
故选:C.
5.C
【分析】
本题考查了菱形的性质,直角三角形斜边中线,掌握菱形对角线互相垂直是解题关键.由菱形的性质可知,,再根据直角三角形斜边中线等于斜边一半,即可求出的长.
【详解】解:四边形是菱形,且周长为72,
,,
E为的中点,
,
故选:C.
6.D
【分析】
此题考查正方形的性质,连接,根据正方形的性质和勾股定理得出,进而利用三角形中位线定理解答即可.
【详解】
解:连接,如图:
四边形是正方形.
,,
,分别是边,中点,
.
在中,由勾股定理得:.
点、分别是、的中点,
是三角形的中位线,
.
故选:D.
7.A
【分析】
本题考查了矩形的判定,平行四边形的性质,由矩形的判定可直接求解.
【详解】解:四边形是平行四边形,,
四边形是矩形,故选项A符合题意;
四边形是平行四边形,,
四边形是菱形,故选项B不符合题意;
四边形是平行四边形,,
四边形是菱形,故选项C不符合题意;
四边形是平行四边形,
,故选项D不符合题意,
故选:A.
8.A
【分析】本题考查了矩形的性质,等边三角形的性质和判定,直角三角形角所对的直角边等于斜边的一半的性质,熟记各性质是解题的关键.
首先证明出是等边三角形,然后得到,然后利用,直角三角形角所对的直角边等于斜边的一半求解即可.
【详解】∵四边形是矩形
∴,
∵
∴是等边三角形
∴
∴
∴.
故选:A.
9.B
【分析】
本题考查正方形的性质,全等三角形的判定和性质,斜边上的中线,过点作,证明,得到为的中点,连接,根据斜边上的中线等于斜边的一半,求出的长,再证明,即可.
【详解】解:∵正方形,,
∴,
∵,,
∴,
∴,
∴,
∴;
过点作,
则:,,
∵,
∴为等腰直角三角形,
∴,
又,
∴,
∴,
连接,则:;
∵,
∴,
∴;
故选:B.
10.C
【分析】
本题考查矩形的性质、折叠的性质、勾股定理,根据矩形的性质和折叠的性质得到,利用勾股定理算出,设,则,,在中,根据勾股定理建立方程求解,即可解题.
【详解】解:当P、E、D三点在同一条直线上,如图所示:
在矩形中,,,,
根据折叠的性质,可得,,,
,
在中,根据勾股定理,得,
设,则,,
在中,根据勾股定理,得,
解得,
,
故选:C.
11.6
【分析】
本题考查矩形的性质,根据矩形的对角线相等,即可得出结果.
【详解】解:∵线段为矩形的对角线,,
∴;
故答案为:6.
12.
【分析】本题考查矩形的性质,等边三角形的判定和性质,以及勾股定理.熟练掌握矩形的对角线相等且平分,是解题的关键.先证明是等边三角形,求出,进而求出,利用即可得解.
【详解】解:∵四边形为矩形,
∴,
∵,点E恰好为的中点,
∴,
∴是等边三角形,
∴
∴,,
∴矩形的面积为;
故答案为:.
13.平行
【分析】本题考查了平行四边形的判定,根据两组对边分别平行的四边形是平行四边形即可求解,掌握平行四边形的判定定理是解题的关键.
【详解】解:∵两组对边分别平行的四边形是平行四边形,
∴当木棒平行木棒时,木棒围城的四边形是平行四边形,
故答案为:平行.
14.6
【分析】本题考查了直角三角形斜边上的中线等于斜边的一半,据此即可解答,熟知该性质是解题的关键.
【详解】解:根据直角三角形斜边上的中线等于斜边的一半,可得斜边为,
故答案为:6.
15.4
【分析】
本题考查矩形的性质,等边三角形的判定和性质,根据矩形的对角线相等且平分,推出为等边三角形,进而得到,即可得出结果.
【详解】解:∵矩形中,对角线交于点O,
∴,
∵,
∴为等边三角形,
∴,
∴;
故答案为:4.
16.
【分析】本题考查了矩形的性质、线段垂直平分线的性质及勾股定理等知识点,数形结合、熟练掌握相关性质及定理是解题的关键.连接,由矩形的性质可得,,,,由,,可知垂直平分,则可得;设,则,在中,由勾股定理得关于的方程,求解即可.
【详解】解:连接,如图:
在矩形中,,,
,,,,
,
,
设,则,
在中,由勾股定理得:,
,
解得:.
故答案为:.
17.16
【分析】
本题主要考查了直角三角形斜边上中线等于斜边的一半,三角形中位线的性质,解题的关键是先根据直角三角形的性质求出,再根据中位线的性质求出,即可得出答案.
【详解】
解:∵在直角中,是斜边上的中线,,
∴.
∵中,D,E分别是,的中点,,
∴是中位线,
∴.
故答案为:16.
18./
【分析】过点作交于点,交于点,根据正方形和等边三角形的性质,得到,,再由勾股定理,求得,进而得到,然后证明四边形是矩形,得到,进而求得,即可求出四边形的面积.
【详解】解:过点作交于点,交于点,
,
四边形是正方形,且边长为2,
,,
是等边三角形,,
,,
由勾股定理得:,
,
四边形是矩形,
,
,
四边形的面积,
故答案为:.
【点睛】本题考查了正方形的性质,等边三角形的性质,矩形的判定和性质,勾股定理等知识,熟练掌握正方形和等边三角形的性质是解题关键.
19.见解析
【分析】由矩形的性质,得出,,,再由等腰三角形的性质得到,进而推出结论.
【详解】四边形矩形,
∴,,,
∵,即是等腰三角形,
∴,
∴,
∴四边形是平行四边形.
【点睛】本题主要考查了平行四边形的性质和判定,等腰三角形的性质,熟记平行四边形的判定和性质是解题的关键.
20.(1)见解析;(2)见解析
【分析】(1)利用基本作图,过点作的垂线即可;
(2)先根据平行四边形的性质得到,所以,再利用垂直的定义得到,接着证明,所以,然后根据平行四边形的判定方法得到四边形是平行四边形.
【详解】(1)解:如图,为所作;
(2)证明:∵四边形是平行四边形,
∴,.
∴.
.
.
∴BE∥DF.
在和中:
.
∴.
,.
∴四边形是平行四边形.
故答案为:, , , .
【点睛】本题考查了作图-复杂作图,全等三角形的判定与性质,平行四边形的判定与性质,解题关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
21.见解析
【分析】根据平行四边形的性质,可得到,,结合点,分别是平行四边形的边,的中点,即可证明结论.
【详解】∵四边形为平行四边形,
∴,.
又点,分别是平行四边形的边,的中点,
∴.
∴四边形为平行四边形.
∴.
【点睛】本题主要考查平行四边形的判定及性质,牢记平行四边形的判定方法和性质是解题的关键.
22.见解析
【分析】
本题考查了平行四边形的性质、全等三角形的判定与性质以及角平分线定义等知识,熟练掌握平行四边形的性质,证明三角形全等是解题的关键.根据平行四边形性质得,,,则,再证明,然后证明,即可得出结论.
【详解】证明:四边形是平行四边形,
,,,
.
平分,平分,
,.
,
在和中,
,
,
.
23.见解析
【分析】此题考查了平行四边形的性质以及全等三角形的判定与性质;由四边形是平行四边形,可得,,继而可证得,即可证得结论.
【详解】证明:四边形是平行四边形,
,,
,
在和中,
,
,
.
24.(1)详见解析
(2)10
【分析】
本题考查菱形的性质,平行四边形的判定和性质,矩形的判定和性质,勾股定理.
(1)先证明四边形是平行四边形,再根据有一个角是直角的平行四边形是矩形,即可得证;
(2)设,在中,利用勾股定理求解即可.
【详解】(1)解:∵菱形,
∴,
∴,
∵,
∴,
∴四边形是平行四边形,
∵,
∴,
∴平行四边形为矩形;
(2)∵菱形,
∴,
∵矩形,
∴,
设,则:,
在中,,
∴,
解得:,
∴.
25.(1)见解析
(2)
【分析】(1)由矩形的性质可得,,结合可得,结合,可证四边形是平行四边形,再根据可证四边形是菱形;
(2)先根据已知条件和(1)中结论证明是等边三角形,进而求出,,再利用勾股定理解即可.
【详解】(1)证明:四边形是矩形,
,,
,
,
,
四边形是平行四边形.
,
平行四边形是菱形.
(2)解:如图,连接,
四边形是菱形,
,,,
,
,
,
是等边三角形,
,,
,
,
,
四边形是矩形,
,,
.
【点睛】本题考查菱形的判定和性质,等边三角形的判定和性质,矩形的性质,勾股定理解直角三角形等,难度一般,解题的关键是掌握菱形的判定方法.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学七年级平行四边形(人教版(五四制))单元测试 基础卷 含解析
学校:___________姓名:___________班级:___________考号:___________
一、单选题(共30分)
1.(本题3分)如图,在中,,,,则的面积为( )
A.30 B.60 C.65 D.
2.(本题3分)如图,有两条相互垂直的卡槽,一小哥将一根木棒的两端分别卡在卡槽中,在木棒的中部插有一支记号笔,接着移动木棒的一端,另一端也随之移动.我们惊讶地发现:记号笔画出了一段圆弧!根据你所学的有关直角三角形的知识,分析“木棒作弧”中所运用的数学道理是( )
A.直角三角形的两直角边长度的平方和等于第三边长度的平方
B.直角三角形的面积等于两直角边乘积的一半
C.直角三角形的两个锐角互余
D.直角三角形斜边上的中线等于斜边的一半
3.(本题3分)如图,在四边形中,,,点E为的中点,连结,若四边形的面积为16,则的面积为( )
A.2 B.4 C.8 D.16
4.(本题3分)如图,平行四边形的对角线相交于点O,下列说法正确的是( )
A. B. C. D.
5.(本题3分)如图,菱形的对角线相交于点O,E为的中点,连接.若菱形的周长为72,则的长为( )
A.3 B.6 C.9 D.12
6.(本题3分)如图,在正方形中,,点、分别是边、的中点,连接、,点,分别是,的中点,则的长为( )
A. B.1 C. D.
7.(本题3分)如图,平行四边形中,增加一个条件,能判定它是矩形的是( )
A. B. C. D.
8.(本题3分)如图,在矩形中,对角线,交于点O,若,,则对角线的长是( )
A.4 B.3 C.2 D.1
9.(本题3分)如图,在正方形中,,点E是延长线上一点,点F是上的点,,,连接交于点,连接,则线段的长是( )
A. B. C. D.
10.(本题3分)在矩形中,,,点P是线段上一个动点,若将沿折叠,使点B落在点E处,连结、,若P、E、D三点在同一条直线上,则的长度是( )
A.1 B.1.5 C.2 D.0.5
二、填空题(共24分)
11.(本题3分)线段为矩形的对角线,若,则的长为 .
12.(本题3分)如图,在矩形中,对角线与相交于点O,过点A作,点E恰好为的中点,,则矩形的面积为 .
13.(本题3分)如图,木棒平行于木棒,当木棒 木棒时,木棒围城的四边形是平行四边形.
14.(本题3分)在中,若斜边上的中线为3,则斜边为 .
15.(本题3分)如图,在矩形中,对角线交于点O,若,则对角线的长是 .
16.(本题3分)如图,矩形的对角线、相交于点O,过点O作交于点E,若,,则 .
17.(本题3分)如图,中,D,E分别是,的中点,F是延长线上的一点,且,若,,则的长为 .
18.(本题3分)如图,正方形的边长为2,是等边三角形,则四边形的面积等于 .
三、解答题(共66分)
19.(本题8分)如图,在矩形中,点在的延长线上,,求证:四边形是平行四边形.
20.(本题8分)如图,在平行四边形中,连接对角线,过点作于点.
(1)用尺规完成以下基本作图:过点作的垂线,垂足为.(保留作图痕迹,不写作法)
(2)在(1)问所作的图形中,连接,求证:四边形是平行四边形.
证明:
∵四边形是平行四边形,
∴ ,.
∴ .
.
.
∴ .
在和中:
.
∴ .
,.
∴四边形是平行四边形.
21.(本题10分)已知点,分别是平行四边形的边,的中点.求证:.
22.(本题10分)如图,在平行四边形中,的平分线交于点E,的平分线交于点F.求证:.
23.(本题10分)如图,的对角线,相交于点,过点且与,分别相交于点,.求证:.
24.(本题10分)如图,过菱形的顶点A作于点E,延长至点F,使,连接.
(1)求证:四边形是矩形;
(2)若,求的长.
25.(本题10分)如图,四边形的对角线,相交于点,,为矩形对角线,.
(1)求证:四边形是菱形;
(2)连接,若,的值.
参考答案:
1.B
【分析】
本题考查的是勾股定理的应用,平行四边形的性质,先证明,再利用勾股定理求解,再利用面积公式进行计算即可.
【详解】
解:∵四边形为平行四边形,
∴.
∵,
∴是直角三角形,
∴,
∴.
故选B.
2.D
【分析】
本题考查了直角三角形的性质,熟记“直角三角形斜边上的中线等于斜边的一半”是解题关键.
【详解】解:因为“木棒作弧”过程中弧上的点到两条相互垂直的卡槽交点距离相等,且木棒作为三角形的斜边,记号笔在木棒的中点,
所以运用了直角三角形斜边上的中线等于斜边的一半,
故选:D.
3.B
【分析】
本题考查的是三角形的中线的性质,平行四边形的判定与性质,先证明四边形是平行四边形,再利用平行四边形的性质与三角形的中线等分三角形的面积可得答案.
【详解】解:∵,,
∴四边形是平行四边形,
∵四边形的面积为16,
∴,
∵点E为的中点,
∴,
故选B
4.C
【分析】本题考查了平行四边形的性质,由平行四边形的性质可得,即可求解,掌握平行四边形的性质是解题的关键.
【详解】∵四边形是平行四边形,
∴,
故选:C.
5.C
【分析】
本题考查了菱形的性质,直角三角形斜边中线,掌握菱形对角线互相垂直是解题关键.由菱形的性质可知,,再根据直角三角形斜边中线等于斜边一半,即可求出的长.
【详解】解:四边形是菱形,且周长为72,
,,
E为的中点,
,
故选:C.
6.D
【分析】
此题考查正方形的性质,连接,根据正方形的性质和勾股定理得出,进而利用三角形中位线定理解答即可.
【详解】
解:连接,如图:
四边形是正方形.
,,
,分别是边,中点,
.
在中,由勾股定理得:.
点、分别是、的中点,
是三角形的中位线,
.
故选:D.
7.A
【分析】
本题考查了矩形的判定,平行四边形的性质,由矩形的判定可直接求解.
【详解】解:四边形是平行四边形,,
四边形是矩形,故选项A符合题意;
四边形是平行四边形,,
四边形是菱形,故选项B不符合题意;
四边形是平行四边形,,
四边形是菱形,故选项C不符合题意;
四边形是平行四边形,
,故选项D不符合题意,
故选:A.
8.A
【分析】本题考查了矩形的性质,等边三角形的性质和判定,直角三角形角所对的直角边等于斜边的一半的性质,熟记各性质是解题的关键.
首先证明出是等边三角形,然后得到,然后利用,直角三角形角所对的直角边等于斜边的一半求解即可.
【详解】∵四边形是矩形
∴,
∵
∴是等边三角形
∴
∴
∴.
故选:A.
9.B
【分析】
本题考查正方形的性质,全等三角形的判定和性质,斜边上的中线,过点作,证明,得到为的中点,连接,根据斜边上的中线等于斜边的一半,求出的长,再证明,即可.
【详解】解:∵正方形,,
∴,
∵,,
∴,
∴,
∴,
∴;
过点作,
则:,,
∵,
∴为等腰直角三角形,
∴,
又,
∴,
∴,
连接,则:;
∵,
∴,
∴;
故选:B.
10.C
【分析】
本题考查矩形的性质、折叠的性质、勾股定理,根据矩形的性质和折叠的性质得到,利用勾股定理算出,设,则,,在中,根据勾股定理建立方程求解,即可解题.
【详解】解:当P、E、D三点在同一条直线上,如图所示:
在矩形中,,,,
根据折叠的性质,可得,,,
,
在中,根据勾股定理,得,
设,则,,
在中,根据勾股定理,得,
解得,
,
故选:C.
11.6
【分析】
本题考查矩形的性质,根据矩形的对角线相等,即可得出结果.
【详解】解:∵线段为矩形的对角线,,
∴;
故答案为:6.
12.
【分析】本题考查矩形的性质,等边三角形的判定和性质,以及勾股定理.熟练掌握矩形的对角线相等且平分,是解题的关键.先证明是等边三角形,求出,进而求出,利用即可得解.
【详解】解:∵四边形为矩形,
∴,
∵,点E恰好为的中点,
∴,
∴是等边三角形,
∴
∴,,
∴矩形的面积为;
故答案为:.
13.平行
【分析】本题考查了平行四边形的判定,根据两组对边分别平行的四边形是平行四边形即可求解,掌握平行四边形的判定定理是解题的关键.
【详解】解:∵两组对边分别平行的四边形是平行四边形,
∴当木棒平行木棒时,木棒围城的四边形是平行四边形,
故答案为:平行.
14.6
【分析】本题考查了直角三角形斜边上的中线等于斜边的一半,据此即可解答,熟知该性质是解题的关键.
【详解】解:根据直角三角形斜边上的中线等于斜边的一半,可得斜边为,
故答案为:6.
15.4
【分析】
本题考查矩形的性质,等边三角形的判定和性质,根据矩形的对角线相等且平分,推出为等边三角形,进而得到,即可得出结果.
【详解】解:∵矩形中,对角线交于点O,
∴,
∵,
∴为等边三角形,
∴,
∴;
故答案为:4.
16.
【分析】本题考查了矩形的性质、线段垂直平分线的性质及勾股定理等知识点,数形结合、熟练掌握相关性质及定理是解题的关键.连接,由矩形的性质可得,,,,由,,可知垂直平分,则可得;设,则,在中,由勾股定理得关于的方程,求解即可.
【详解】解:连接,如图:
在矩形中,,,
,,,,
,
,
设,则,
在中,由勾股定理得:,
,
解得:.
故答案为:.
17.16
【分析】
本题主要考查了直角三角形斜边上中线等于斜边的一半,三角形中位线的性质,解题的关键是先根据直角三角形的性质求出,再根据中位线的性质求出,即可得出答案.
【详解】
解:∵在直角中,是斜边上的中线,,
∴.
∵中,D,E分别是,的中点,,
∴是中位线,
∴.
故答案为:16.
18./
【分析】过点作交于点,交于点,根据正方形和等边三角形的性质,得到,,再由勾股定理,求得,进而得到,然后证明四边形是矩形,得到,进而求得,即可求出四边形的面积.
【详解】解:过点作交于点,交于点,
,
四边形是正方形,且边长为2,
,,
是等边三角形,,
,,
由勾股定理得:,
,
四边形是矩形,
,
,
四边形的面积,
故答案为:.
【点睛】本题考查了正方形的性质,等边三角形的性质,矩形的判定和性质,勾股定理等知识,熟练掌握正方形和等边三角形的性质是解题关键.
19.见解析
【分析】由矩形的性质,得出,,,再由等腰三角形的性质得到,进而推出结论.
【详解】四边形矩形,
∴,,,
∵,即是等腰三角形,
∴,
∴,
∴四边形是平行四边形.
【点睛】本题主要考查了平行四边形的性质和判定,等腰三角形的性质,熟记平行四边形的判定和性质是解题的关键.
20.(1)见解析;(2)见解析
【分析】(1)利用基本作图,过点作的垂线即可;
(2)先根据平行四边形的性质得到,所以,再利用垂直的定义得到,接着证明,所以,然后根据平行四边形的判定方法得到四边形是平行四边形.
【详解】(1)解:如图,为所作;
(2)证明:∵四边形是平行四边形,
∴,.
∴.
.
.
∴BE∥DF.
在和中:
.
∴.
,.
∴四边形是平行四边形.
故答案为:, , , .
【点睛】本题考查了作图-复杂作图,全等三角形的判定与性质,平行四边形的判定与性质,解题关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
21.见解析
【分析】根据平行四边形的性质,可得到,,结合点,分别是平行四边形的边,的中点,即可证明结论.
【详解】∵四边形为平行四边形,
∴,.
又点,分别是平行四边形的边,的中点,
∴.
∴四边形为平行四边形.
∴.
【点睛】本题主要考查平行四边形的判定及性质,牢记平行四边形的判定方法和性质是解题的关键.
22.见解析
【分析】
本题考查了平行四边形的性质、全等三角形的判定与性质以及角平分线定义等知识,熟练掌握平行四边形的性质,证明三角形全等是解题的关键.根据平行四边形性质得,,,则,再证明,然后证明,即可得出结论.
【详解】证明:四边形是平行四边形,
,,,
.
平分,平分,
,.
,
在和中,
,
,
.
23.见解析
【分析】此题考查了平行四边形的性质以及全等三角形的判定与性质;由四边形是平行四边形,可得,,继而可证得,即可证得结论.
【详解】证明:四边形是平行四边形,
,,
,
在和中,
,
,
.
24.(1)详见解析
(2)10
【分析】
本题考查菱形的性质,平行四边形的判定和性质,矩形的判定和性质,勾股定理.
(1)先证明四边形是平行四边形,再根据有一个角是直角的平行四边形是矩形,即可得证;
(2)设,在中,利用勾股定理求解即可.
【详解】(1)解:∵菱形,
∴,
∴,
∵,
∴,
∴四边形是平行四边形,
∵,
∴,
∴平行四边形为矩形;
(2)∵菱形,
∴,
∵矩形,
∴,
设,则:,
在中,,
∴,
解得:,
∴.
25.(1)见解析
(2)
【分析】(1)由矩形的性质可得,,结合可得,结合,可证四边形是平行四边形,再根据可证四边形是菱形;
(2)先根据已知条件和(1)中结论证明是等边三角形,进而求出,,再利用勾股定理解即可.
【详解】(1)证明:四边形是矩形,
,,
,
,
,
四边形是平行四边形.
,
平行四边形是菱形.
(2)解:如图,连接,
四边形是菱形,
,,,
,
,
,
是等边三角形,
,,
,
,
,
四边形是矩形,
,,
.
【点睛】本题考查菱形的判定和性质,等边三角形的判定和性质,矩形的性质,勾股定理解直角三角形等,难度一般,解题的关键是掌握菱形的判定方法.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
