福建省莆田第八中学(人教版)数学高一下学期必修二课件:1-3-2球的表面积与体积(共17张PPT)
文档属性
| 名称 | 福建省莆田第八中学(人教版)数学高一下学期必修二课件:1-3-2球的表面积与体积(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 620.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-21 00:00:00 | ||
图片预览





文档简介
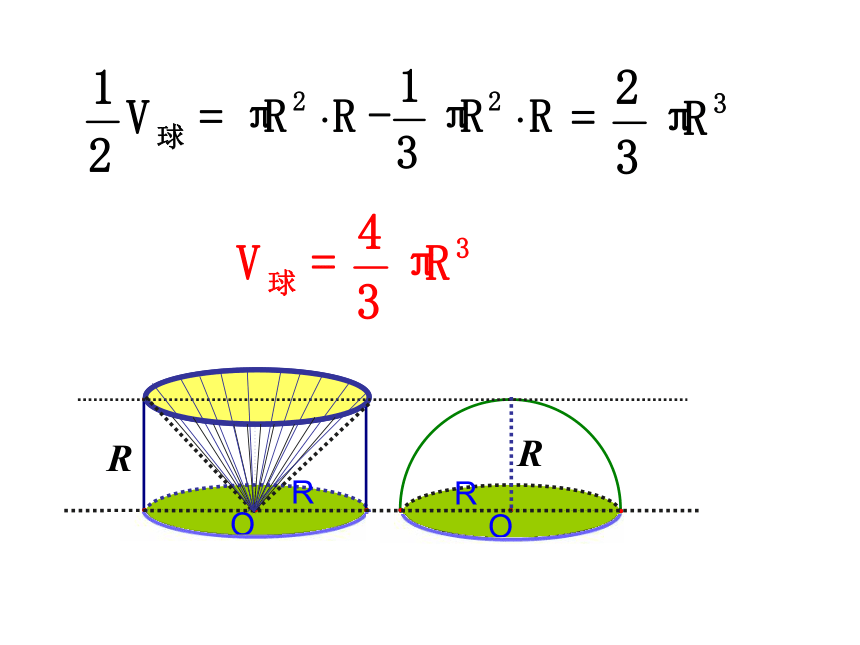
课件17张PPT。1.3.2球的表面积与体积数学组 程金镇学习目标:1、通过对球的体积和面积公式的推导, 了解推导过程中所用的基本数学思想方法:“分割—求和—化为准确和”;
2、能运用球的面积和体积公式灵活解决实际问题;
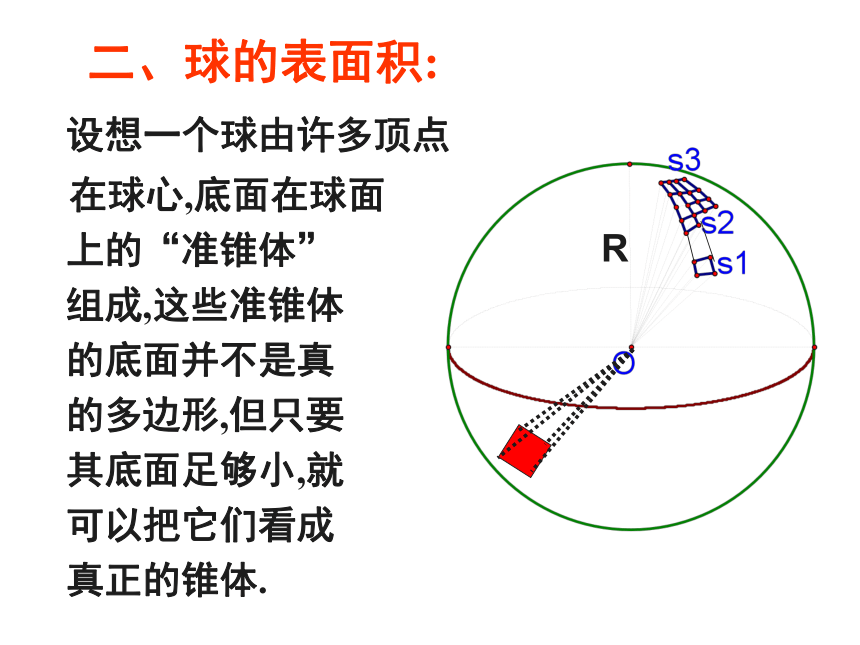
3、能解决球的截面有关计算问题及球的 “内接”与“外切”的几何体问题。RR一个半径和高都等于R的圆柱,挖去一个以上底面为底面,下底面圆心为顶点的圆锥后,所得的几何体的体积与一个半径为R的半球的体积相等。一、球的体积:RRR二、球的表面积:RS球表=4πR2例1:钢球直径是5cm,求它的体积.(变式1)一种空心钢球的质量是142g,外径 是5cm,求它的内径.(钢的密度是7.9g/cm2)解:设空心钢球的内径为2xcm,则钢球的质量是答:空心钢球的内径约为4.5cm.由计算器算得:(变式1)一种空心钢球的质量是142g,外径 是5cm,求它的内径.(钢的密度是7.9g/cm2)(变式2)把钢球放入一个正方体的有盖纸盒中,至少要用多少纸?用料最省时,球与正方体有什么位置关系?侧棱长为5cm两个几何体相切:一个几何体的各个面与另一个几何体的各面相切.球内切于正方体(变式3)把正方体的纸盒装入半径为4cm的球状木盒里,能否装得下?半径为4cm的木盒能装下的最大正方体 与球盒有什么位置关系?球外接于正方体两个几何体相接:一个几何体的所有顶点都在
另一个几何体的表面上。82.有三个球,一球切于正方体的各面,一球切于正方体的各侧棱,一球过正方体的各顶点,求这三个球的体积之比_________.1.球的直径伸长为原来的2倍,体积变为原来的_倍.练习1:探究:若正方体的棱长为a,则:
(1)正方体的内切球的直径=
(2)正方体的外接球的直径=
(3)与正方体所有的棱相切的球的直径=4.若两球体积之比是1:2,则其表面积之比是______.练习2:1.若球的表面积变为原来的2倍,则半径变为原来
的___倍.2.若球半径变为原来的2倍,则表面积变为原来
的___倍.3.若两球表面积之比为1:2,则其体积之比是___.7.将半径为1和2的两个铅球,熔成一个大铅球,
那么这个大铅球的表面积是______.6.若两球表面积之差为48π ,它们大圆周长之和为12π ,则两球的直径之差为______.练习2:5.长方体的共顶点的三个侧面积分别为 ,
则它的外接球的表面积为_____.例2:如图是一个奖杯的三视图,单位是cm,
试画出它的直观图,并计算这个奖杯的体积.
(精确到0.01cm)86618515151111x/y/z/解:这个奖杯的体积为V=V正四棱台+V长方体+ V球 V正四棱台V长方体=6×8×18=864V球=所以这个奖杯的体积为V ≈ 1828.76(cm3)【总一总★成竹在胸】1.球的表面积公式;
2.球的体积公式.再见
2、能运用球的面积和体积公式灵活解决实际问题;
3、能解决球的截面有关计算问题及球的 “内接”与“外切”的几何体问题。RR一个半径和高都等于R的圆柱,挖去一个以上底面为底面,下底面圆心为顶点的圆锥后,所得的几何体的体积与一个半径为R的半球的体积相等。一、球的体积:RRR二、球的表面积:RS球表=4πR2例1:钢球直径是5cm,求它的体积.(变式1)一种空心钢球的质量是142g,外径 是5cm,求它的内径.(钢的密度是7.9g/cm2)解:设空心钢球的内径为2xcm,则钢球的质量是答:空心钢球的内径约为4.5cm.由计算器算得:(变式1)一种空心钢球的质量是142g,外径 是5cm,求它的内径.(钢的密度是7.9g/cm2)(变式2)把钢球放入一个正方体的有盖纸盒中,至少要用多少纸?用料最省时,球与正方体有什么位置关系?侧棱长为5cm两个几何体相切:一个几何体的各个面与另一个几何体的各面相切.球内切于正方体(变式3)把正方体的纸盒装入半径为4cm的球状木盒里,能否装得下?半径为4cm的木盒能装下的最大正方体 与球盒有什么位置关系?球外接于正方体两个几何体相接:一个几何体的所有顶点都在
另一个几何体的表面上。82.有三个球,一球切于正方体的各面,一球切于正方体的各侧棱,一球过正方体的各顶点,求这三个球的体积之比_________.1.球的直径伸长为原来的2倍,体积变为原来的_倍.练习1:探究:若正方体的棱长为a,则:
(1)正方体的内切球的直径=
(2)正方体的外接球的直径=
(3)与正方体所有的棱相切的球的直径=4.若两球体积之比是1:2,则其表面积之比是______.练习2:1.若球的表面积变为原来的2倍,则半径变为原来
的___倍.2.若球半径变为原来的2倍,则表面积变为原来
的___倍.3.若两球表面积之比为1:2,则其体积之比是___.7.将半径为1和2的两个铅球,熔成一个大铅球,
那么这个大铅球的表面积是______.6.若两球表面积之差为48π ,它们大圆周长之和为12π ,则两球的直径之差为______.练习2:5.长方体的共顶点的三个侧面积分别为 ,
则它的外接球的表面积为_____.例2:如图是一个奖杯的三视图,单位是cm,
试画出它的直观图,并计算这个奖杯的体积.
(精确到0.01cm)86618515151111x/y/z/解:这个奖杯的体积为V=V正四棱台+V长方体+ V球 V正四棱台V长方体=6×8×18=864V球=所以这个奖杯的体积为V ≈ 1828.76(cm3)【总一总★成竹在胸】1.球的表面积公式;
2.球的体积公式.再见
